1.瞬态过程的概念
（1）稳定状态
所谓稳定状态就是指电路中的电压、电流已经达到某一稳定值，即电压和电流为恒定不变的直流或者是最大值与频率固定的正弦交流。
（2）瞬态过程
电路从一种稳定状态向另一种稳定状态的转变，这个过程称为瞬态过程，也称为过渡过程。电路在瞬态过程中的状态称为瞬态。
为了了解电路产生瞬态过程的原因，我们观察一个实验现象。图7.1所示电路，三个并联支路分别为电阻、电感、电容与灯泡串联，S为电源开关。
当闭合开关S时我们发现电阻支路的灯泡EL1立即发光，且亮度不再变化，说明这一支路没有经历瞬态过程，立即进入了新的稳态；电感支路的灯泡EL2由暗渐渐变亮，最后达到稳定，说明电感支路经历了瞬态过程；电容支路的灯泡EL3由亮变暗直到熄灭,说
图7.1瞬态过程演示实验
明电容支路也经历了瞬态过程。当然若开关S状态保持不变（断开或闭合），我们就观察不到这些现象。由此可知，产生瞬态过程的外因是接通了开关，但接通开关并非都会引起瞬态过程，如电阻支路。产生瞬态过程的两条支路都存在有储能元件（电感或电容），这是产生瞬态过程的内因。
（3）换路
通常把电路状态的改变（如通电、断电、短路、电信号突变、电路参数的变化等），统称为换路，并认为换路是立即完成的。
综上所述，产生瞬态过程的原因有两个方面，即外因和内因。换路是外因，电路中有储能元件（也叫动态元件）是内因。所以瞬态过程的物理实质，在于换路迫使电路中的储能元件要进行能量的转移或重新再分配，而能量的变化又不能从一种状态跳跃式地直接变到另一种状态，必须经历一个逐渐变化过程。
2.换路定律
分析电路的瞬态过程时，除应用基尔霍夫定律和元件伏安关系外还应了解和利用电路在换路时所遵循的规律（即换路定律）。
为便于电路分析，特作如下设定：t＝0为换路瞬间，而以t=0－表示换路前的终了时间，t=0＋表示换路后的初始瞬间。0－和0＋在数值上都等于0，但前者是指t从负值趋进于零，后者是指t从正值趋进于零。
（1）电感元件 由于它所储存的磁场能量
在换路的瞬间保持不变，因此可得
iL(0+)=iL(0－)
（2）电容元件 由于它所储存的电场能量
在换路的瞬间保持不变，因此可得
uC(0+)=uC(0－)
综上所述，换路时，电容电压uC不能突变；电感电流iL不能突变。这一结论叫做换路定律。即
uC(0+)=uC(0－)
iL(0+)=iL(0－)
需要强调的是，电路在换路时，只是电容电压和电感电流不能跃变，而电路中其它的电压和电流是可以跃变的。
3.一阶电路初始值的计算
（1）一阶电路 只含有一个储能元件的电路称为一阶电路。
（2）初始值 我们把t=0+时刻电路中电压、电流的值，称为初始值。
（3）电路瞬态过程初始值的计算按下面步骤进行：
①根据换路前的电路求出换路前瞬间，即t=0－时的电容电压uC(0－)和电感电流iL(0－)值；
②根据换路定律求出换路后瞬间，即t=0+时的电容电压uC(0+)和电感电流iL(0+)值；
③画出t＝0＋时的等效电路，把uC(0+)等效为电压源，把iL(0+)等效为电流源；
④求电路其它电压和电流在t＝0＋时的数值。
例7.2 图7.3（a）中，直流电压源的电压Us=50V，R1=5Ω，R2=5Ω，R3=20Ω，电路原已达到稳态，在t=0时，断开开关S，试求0＋时的iL、Uc、 UR、ic、 UL。
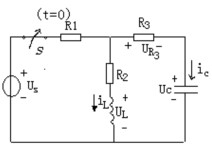
(a)原电路图 (b)t=0+时的等效电路
图7.3 例7.2电路图
