第4节 变压器的负载运行

　　变压器负载运行指变压器一次绕组接额定频率、额定电压的交流电源，二次绕组接负载的运行状态。

　　一、负载运行时的电磁过程

　　

 

　　图1.4.2-1 单相变压器负载运行图

　　变压器二次绕组接负载ZL,二次绕组有电流2 流过，输出 电压2=2ZL ;电流2 建立二次磁动势2=2N2，作用在主磁路上，企图改变主磁通 。

　　电源电压1不变时，主磁通基本不变。一次绕组的电流 必须相应由增大为1 ，一次磁动势也由0 增 大为1=1N1，以抵消二次磁动势对主磁通的影响， 从而保持主磁通不变。

 1和2 除共同建立主磁通外，还分别产生交链各自绕组的漏 磁通1σ和2σ,并在一、二次绕组中感应漏电动势1σ和2σ。
1σ和2σ可以用漏抗压降的形式来表示：。

 

　　x2称为二次绕组的漏抗，与二次绕组漏磁通相对应，为常量，

。

 

　　一、二次绕组电流分别在一、二次绕组电阻上产生压降1r1 和2r2.

　　变压器负载运行时各物理量的关系总结如下：

　　

 

　　二、负载运行时的方程式

　　磁动势平衡方程式

　　负载时建立主磁通的磁动势为

1 和2 空载时建立主磁通的磁动势为0 空载到负载，主磁通基本不变 → 磁动势平衡方程式 1+2 =0

 

　　

 

　　一、二次绕组的电流与其匝数成反比，变压器变压的同时也改变 了电流的大小。

　　电动势平衡方程式

　　根据基尔霍夫第二定律，参照图1.4.2-1所示参考正方向负载运行时各物理量的关系，可得一、二次绕组的电 动势平衡方程式

　　

 

　　三、绕组折算

　　变压器一、二次绕组间只有磁耦合，没有电联系，分析、计算 很不方便。为得到一、二次绕组间有电联系的等效电路，需要引入绕组折算的概念。

　　在变压器中，习惯把二次绕组折算到一次绕组，即用一个与一次绕组匝数相等的假想二次绕组代替实际的二次绕组，并在折算过程中满足"等效"的原则。所谓"等效"是指折算部分折算前后对未折算部分作用相同，并且折算部分折算前后各物理量的关系和功率不变(包括有功功率和无功功率)。习惯用原物理量右上角加一撇"'" 来表示折算后的物理量。下面根据折算的原则，导出二次绕组折算前后各物理量的关系。

　　电流的折算若折算前后二次磁动势不变，则二次绕组对一次绕组的作用就不变，满足折算的"等效"原则。

　　

 

　　二次绕组折算到一次绕组，凡单位是伏特的物理量折算后的值等于折算前的值乘以变比k，凡单位是安培的物理量折算后的值等于折算前的值除以变比k，凡单位是欧姆的物理量折算后的值等于折算前的值乘以k*k 。

　　折算后的基本方程式组

　　

 

　　四、负载运行时的等效电路

　　由折算后的基本方程式组可画出变压器负载运行时的等效电路如图1.4.5-1所示。图中一次绕组漏阻抗

、二次绕组漏阻抗 和激磁阻抗 所在的三条支路呈"T" 字型,称为T型等效电路。它是变压器最基本的等效电路，能准确反映变压器内部电磁关系，但它是混联电路，进行复数运算比较麻烦。

 

　　

 

　　图1.4.5-1 变压器的T型等效电路

　　一次绕组漏阻抗很小，通常将激磁支路移到一次绕组漏阻抗前， 得到如图1.4.5-2所示的近似等效电路。近似等效电路是并联电路，可大大简化计算，常用来定量计算。

　　

 

　　图1.4.5-2 变压器的近似等效电路

　　激磁电流很小，在T型等效电路中去掉激磁支路，可得更简单的串联电路，如图1.4.5-3所示，称为简化等效电路，常用来定性分析。

　　

 

　　图1.4.5-3 变压器的简化等效电路

　　图1.4.5-3中，

，称为短路电阻; ， 称为短路电抗; ，称为短路阻抗。短路阻抗为漏阻抗参数，数值较小且为常数。

 

　　根据基尔霍夫第二定律，参照图1.4.5-3简化等效电路所示的参 考正方向，可得与其相应的电压平衡方程式如下:

 

　　五、负载运行时的相量图

　　不同的等效电路对应不同的方程式组，因此有不同的相量图。下面主要介绍T型等效电路和简化等效电路的相量图。

　　T型等效电路的相量图

　　

 

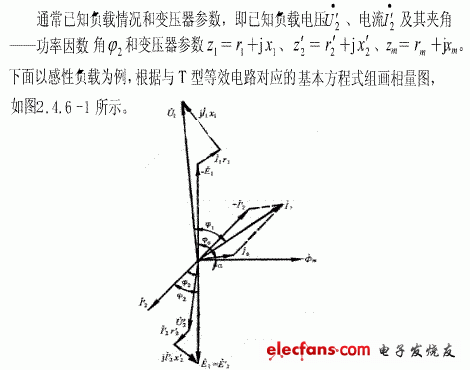
　　图1.4.6-1 变压器带感性负载运行时的相量图

　　作图步骤如下：

　　

 

　　简化等效电路的相量图

　　简化相量图也以感性负载为例，根据与简化等效电路对应 的电压方程式画相量图。

　　

 

　　图1.4.6-2 变压器带感性负载运行时的简化相量图