大数据的挑战与随机机器学习算法

　数据规模的重要性
　　数据在不断地增长，数据量很大的时候是非常重要的一件事情，因为数据只有到了一定的程度的量才会发生质的变化，有一个例子是Matrix Completion（矩阵补全），就是给你一个表，有一部分的数据你知道，有一部分数据你不知道，没有办法拆出来，这个东西就是矩阵补全。矩阵补全非常重要，几乎所有的机器学习的问题都可以表示成矩阵补全的问题，这里显示的聚类，也可以看成矩阵补全。
　　矩阵补全非常有意思的结果是怎样的？我们这边的横轴是数据量，考虑在矩阵里能够看到的数据量，纵轴是恢复误差，拆出来的结果和真实结果的误差，肯定是数据量越多拆的误差越高，当数据低于一定程度的时候，这可以是非常显示的刻划出来，在数据小于一定量的时候，不管怎么做总是拆的很糟糕，几乎没有太大的区别。只有当你的数据大于一定量的时候，突然你可以拆的非常准，如果按原来的说法，在一个的情况下，你可以拆的很完美，没有任何的错误。所以我们说大数据，只有当数据到一定的程度的时候，有些事情才是可能的，当你的数据小于这个的时候，不管你怎么做都永远不可能。
　　大数据带来的困难我们大家一直在谈大数据的挑战，来到阿里之前我没有意识到，来了之后觉得这个事情真的是big deal。做任何统计是最重要的一件事情，比如这里非常基础、简单的任务——矩阵平均，即便只是简简单单地做大数据下的平均，也是一个big deal，每一个矩阵都是很大（1Bx1M）。在应用里头，这个矩阵记录了每个人对每个商品行为的矩阵，这个矩阵是非常大的，但每天记录下的矩阵是很稀疏的，虽然说你有几百万几千万的商品，但通常每个人只有在很少量的商品上的行为，你希望把这些矩阵加起来，平均表达出在一个人在很长的周期内的行为是什么样的，但是一个disaster就发生了，如果矩阵做一个平均、求和，这个矩阵会变成一个death的矩阵，如果不做任何smart commutation，这个事情实际上是非常昂贵的，而且存储也是昂贵的。我在阿里的第一件事情，就是我能不能做一个这样的平均，我虽然不能算出确切结果，但有没有办法说我可以算出大概结果？最后一个很简单的办法，就是用一个随机算法做这个事情。
　　随机算法的好处所谓的机器学习问题（Learning Problem），一般的机器学习问题会写成这样的形式，考虑有一堆训练样本，有一个叫Lost Function，用来比较预测和现实的差别，并分析这些差别。通常，Learning Problem就是找到一个解，确认这个解能够给出正确的预测和训练样本，通常可以把它变成一个优化问题来做。
　　
　　解决该问题的主要挑战在于两个方面：一个方面是样本数量很大（1Bx1M），还有一个问题是维度非常高，通常来讲都是亿级，要解决的不会是一个简单的问题。一个成熟的解决方案就是随机算法。相信很多人都有意无意地使用到随机算法，比如用LR、SGD。
　　随机算法有两个好处：
　　随机算法的Efficient，包括两个方面，第一个方面是即使针对大规模样本也不需要多次扫描数据，另一个方面，如果是非常高维的数据，一个简单的办法是可以使用随机投影（Random Projection）来降低维度，这样可以不用直接解决高维问题；随机算法的Effective，就是它通常有最小化泛化误差 （Generalization Error） ，不仅仅是计算简化，同时也可以提供很强的保证。
　　随机算法的挑战（以随机投影为例）
　　随机算法很好，但是总体来讲，随机算法还是有很多的局限的，我的演讲用一个很简单的随机投影问题来讨论，来看一下随机算法的问题在哪里。
　　随机投影是一种非常简单的方法，而且应用广泛。一个高维矩阵X，long long vector，处理起来很麻烦，计算量很大，而且可以证明优化收敛速度跟维度是有关系的。一个简单的做法，针对非常长的vector，乘上一个非常fat的随机矩阵S，乘完以后得到一个很短vector的X point，很低维度的表示，就把这个X point变成我的数据，用低维的数据来优化问题，在低维空间学习。这个好的解是一个很矮的vector，我还要回到原来的空间上去，把原来的矩阵转置一下，又变成一个很长的vector，就变成最后的解。几乎所有的random projection都可以这么做：把一个（很长的）vector用一个随机矩阵变成一个很短很短的vector，算出一个解来，再把矩阵转置，把最优解一乘就可以了。这是一个非常简单的算法，是使用广泛，而且有无限多的paper分析这个东西有没有效。几乎所有的paper都告诉你这个东西很有效，也可以证明它很有效，但是我觉得所有的paper都很理想化，通常会假设原来的问题是一个很容易解的问题，可以证明所有的东西都是对的，但不幸的是，如果你的问题是比较难分类的问题，它告诉你的所有story都是假的。所以这其中隐藏了一个非常有趣的几何泛函的问题，一百多年前就已经被well study。也就是说，这个W star是真正的最优解，把所有的高维数据放进去让机器run获得的最优解，而所有W star cute就是刚才说的用随机投影的算法降维得到的解，你可以证明这两个解通常会有非常大的差别，这个差别跟原来的vector应该是一个数量级的。
　　
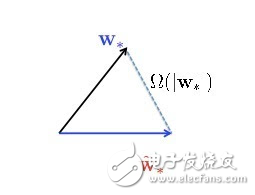
　　所以说run随机投影的算法拿到的解，跟原来的解有很大的差别。这是不是因为我描述了一个非常特定的过程，这个中间的过程造成这个解不好，所以是不是尝试一下变化一个问题就有机会拿到更好的解呢？非常不幸地告诉你，这是不可能的，这也就是我说的Impossibility Theorem，可以证明这个事情不管怎么玩，只要做随机投影，不管你怎么去解这个w star cute，这两个解永远是差别很大，这和怎么解的问题都没有半毛钱关系。而且非常奇怪这个东西一百多年前都知道了，不知道为什么没有人提出来。但是对我来说这个事情很有意思，我能不能做其他的事情，稍微加一点限制，就能让我这个疏密的问题解掉？
　　对偶随机投影的优化
　　这是五年前让我很感兴趣的一个问题，我们创造了一个对偶随机投影 （Dual Random Projection），非常简单、非常神奇，把随机投影得到的w star cute这个解塞到每一个Lost Function里去，然后去求一个导数，这里称为alpha i，最后的解是用每一个training instance和alpha i对应，所以你需要做的，不是直接采用随机投影得到的解，而是用随机投影的解去算它的对偶变量，用对偶变量去win每一个training instance。