增广链修复的最大流求解算法

　　最大流问题是运筹学中经典问题之一，它可以使用图的方法进行求解。网络最大流在计算机、工程学等学科中有着广泛的用途，例如通信网络流量分配、交通运输线路分配等都能转化为网络最大流数学模型。最大流的经典算法主要分为增广链法和预流推进法，其中常用的增广链法有Ford-Fulkerson提出的增广链算法、Dinic研究的阻塞流和分层网络算法、Edmonds等设计的最短路增广算法、Karzanov改进的先进先出预流推进算法及Cherkassky改进的最高标号预流推进算法。这些经典算法逐渐降低了求解网络最大流的时间复杂度，是研究大规模网络的基础。

　　经典算法的经典之处在于它的适用面广，在各类网络中都能稳定运行且在较短时间内完成求解过程，但在部分特殊网络如稀疏网络中，它们的效率不高，因此需针对这些网络的特点改进或使用新算法提高执行效率，实现其研究价值。

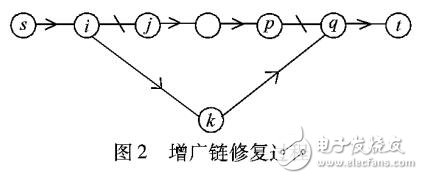
　　本文针对Newman和Watts提出的NW小世界网络以及Barabasi和Albert提出的BA无标度网络两种现实中常见的网络提出了一种新算法，这种算法能够尽可能地避免反复地重新寻找新的增广链，通逋捷径的方法修复满足条件的原始增广链，从而缩短了重复计算的时间，提高算法效率。