导读
所谓人脸融合:给定输入人脸A、B,输出的人脸C具有A和B共同的特征,是一张全新的人脸,也可以说是一张假脸。 人脸融合的过程主要有三步:人脸特征点定位,人脸融合,人脸交换。
第一步,通过深度学习训练的模型对两张待融合的图像进行关键点定位;
第二步,根据定位结果对人脸进行融合;
第三步,将融合得到的人脸交换到待交换的人脸上,合成最终图像。
实际上做到第二步已经达到了人脸融合的基本要求,对于人脸交换,大部分用于假脸交换起到一定的隐私保护作用,用在人脸融合这里也算刚刚好,如果随意用于交换真脸,那就是信息灾难了,例如各种换脸的视频电影层出不穷。
1 人脸特征点定位
1.1 训练模型
数据集越大,训练的模型越精确。人脸特征点检测有一个非常著名的数据集300-W(300 Faces In-The-Wild Challenge)。300-W是一项专注于人脸特征点的检测的竞赛,在该竞赛中,参赛队伍需要从600张图片中检测出人脸,并且将面部的68个特征点全部标记出来。300W数据的压缩包有2G多。包含各种各样已经标记好的人脸信息。因为在如此大的数据集上训练需要大量的资源和时间。所以,在本次的设计中,我们使用少量的数据集来训练。 训练特征点检测模型,这里我们用到了imglab工具。Imglab用于标记可用于训练dlib或其他对象检测器的对象的图像。通过cmd:
imglab -c training_with_face_landmarks.xml images 来创建我们记录标签的xml文件,接下来通过cmd:
imglab training_with_face_landmarks.xml 打开imglab工具对图像打标签。这里我们按照dlib官方给出的68个特征点对每张图片进行标注,shift+鼠标左键拖动截取人脸,双击选择的矩形,shift+左键进行特征点标注。 接下来就可以开始训练模型,这一步就看电脑性能了。首先定义参数设置函数:
options = dlib.simple_object_detector_training_options() 大部分参数,我们使用默认值,针对我们的训练集,主要设定如下几个参数。
Oversampling_amount: 通过对训练样本进行随机变形扩大样本数目。比如N张训练图片,通过设置该参数,训练样本数将变成N * oversampling_amount张。所以一般而言,值越大越好,只是训练耗时也会越久。因为本例中训练集数据较少,所以我们将值设得较高(300)。
Nu: 正则项。nu越大,表示对训练样本fit越好。
Tree depth: 树深。本例中通过增加正则化(将nu调小)和使用更小深度的树来降低模型的容量。
Be_verbose,是否输出训练的过程中的相关训练信息,设置为真。
1.2 测试模型
人脸特征点检测模型训练完成后,需要测试该模型的准确率。测试模型的准确率包括两部分,训练集测试和测试集测试。训练集就是训练该模型的数据集合。输出在训练集中的准确率的核心代码为:
print("Training accuracy{0}".format(dlib.test_shape_predictor(training_xml_path,"predictor.dat"))) 测试集即非训练集数据的集合。输出在测试集中的准确率的核心代码为:
print("Testing accuracy:{0}".format(dlib.test_shape_predictor(testing_xml_path, "predictor.dat"))) 1.3 特征点定位 用训练好的模型进行人脸特征点检测。具体步骤如下,导入上述训练好的模型:
predictor = dlib.shape_predictor("predictor.dat"); 检测人脸:
dets = detector(img, 1) 返回人脸所在矩形,可通过len(dets)获得人脸个数;获取检测到的人脸特征点:
lanmarks = [[p.x, p.y] for p in predicator(img1, d).parts()]; 在图片中循环打印出68个特征点,
2 人脸融合
这一步首先介绍两个算法,Delaunay三角剖分,仿射变换。
2.1 Delaunay三角剖分
设点集V,x,y属于点集V,多边形S中两个端点为x,y的一条边e,若过x,y两点存在一个圆,且点集V中任何其他的点都不在该圆内,圆上包括x,y两点最多三点,那么称e为Delaunay边。那么如果点集V的一个三角剖分T只包含Delaunay边,那么该三角剖分称为Delaunay三角剖分。 Delaunay三角剖分有两个重要特性,一个是空接圆特性:Delaunay三角剖分是唯一的,任意四点不能共圆,在Delaunay三角剖分中任一三角形的外接圆范围内不会有其它点存在。另外一个是最大化最小角特性:在散点集形成的所有三角剖分中,Delaunay三角剖分所形成的三角形的最小角最大。 该算法其实来源于美术馆问题,美术馆是一个复杂的多边形,我们需要在美术馆当中安排警卫,在使得他们能观察到美术馆的所有角落前提下,安排的警卫最少。多边形中的视野问题不好处理,所以将多边形剖分成多个三角形从而使问题得到简化。警卫站在三角形的任意一个位置都能观察到这个三角形中的每一个点。数学家Steve Fisk对这个问题给出了非常精彩的解答:剖分成三角形后,每个三角形的三个顶点共用三种不同的颜色染色,染色结束后在最少的颜色上设置警卫即可,如下图所示。
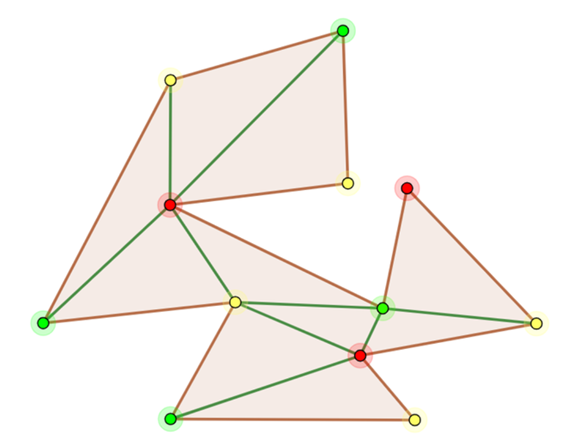
所以问题简化成将该多边形剖分成一个个三角形。另外三角剖分也有优劣之分,一般来说,剖分出来的三角形越匀称越好,匀称的三角形在图形图像处理方面效果比陡峭的三角形更好,如下图所示,都是对同一个六边形进行三角剖分,但是右边的效果更好,这就是Delaunay三角剖分。而在人脸融合技术中,Delaunay三角剖分也扮演了不可或缺的角色。
我们根据得到的特征点对人脸进行Delaunay三角剖分,将人脸剖分成一个个三角形,然后将一个个三角形进行仿射变换,再调整透图片透明度,便可得到融合后的人脸,训练的特征点越多,融合的效果便越好。OpenCV提供了Subdiv2D类实现了Delaunay三角剖分算法,subdiv = cv2.Subdiv2D(rect),将68个特征点的位置插入subdiv,subdiv.insert§ ,获取Delaunay三角列表:
trangleList = subdiv.getTriangleList() 最后调用cv2.line()将剖分后的结果画出,
2.2 仿射变换
仿射变换,又称仿射映射,是指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。仿射变换能够保持图像的“平直性”,包括旋转,缩放,平移,错切操作。一般而言,仿射变换矩阵为2*3的矩阵,第三列的元素起着平移的作用:
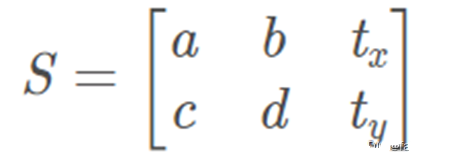
前面两列的数字对角线上是缩放,其余为旋转或者错切的作用。仿射变换是一种二维坐标(x, y)到二维坐标(xt, yt)的线性变换。数学表达式如下图所示:
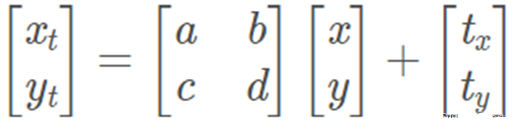
直观的图像表示就是这样:

首先对之前得到的特征点进行预处理。人脸特征点检测算法得出的人脸68个特征点保存在本地的txt文件中。同时,Delaunay三角剖分算法得到的三角形的索引结点也保存在本地的txt文件中。读取人脸A的特征点points1,人脸B的特征点points2。因为要求融合的人脸不一定是同等大小,所以我们取一个平均值保存在points中。Points即为我们融合后的人脸特征点所在位置。经过三角剖分后,人脸被剖分成一个个三角形。我们从保存的三角形索引结点中循环读取每一个三角形的索引点,通过索引结点找到人脸A和人脸B的该三角形所对应的三个特征点位置。取得的三角形以下称三角形A,三角形B。取平均值的三角形称为C。因为做仿射变换只需要变换一个我们剖分形成的三角形,不需要变换整张图片,所以我们可以求得该三角形的最小外接矩形,以提升变换效率,并减少计算量。
r = cv2.boundingRect(np.float32([t])) 返回的r为一个四元组,前两个值为矩形左上角的坐标,后两个值为矩形的长和宽。因为要在上面获得的外接矩形中进行仿射变换,所以原点从图片的左上角点变成了外接矩形的左上角点,从而要修改三角形的三点坐标。
tRect.append(((t[i][0] - r[0]), (t[i][1] - r[1]))) t为预处理中获得的三角形三个顶点坐标。在上一步中,我们获得了输出矩形图像。但是,我们对矩形区域内的三角形感兴趣。因此,我们使用fillConvexPoly创建一个掩模mask,用于遮蔽三角形外的所有像素。这个新的裁剪图像最终可以使用输出边界矩形的左上角坐标点置于输出图像中的正确位置。接下来就是通过仿射变换将三角形A,B变换到C的位置上。
warpImage1 = applyAffineTransform(img1Rect, t1Rect, tRect, size)warpImage2 = applyAffineTransform(img2Rect, t2Rect, tRect, size) ApplyAffineTransform是手写的函数,包括cv2.getAffineTransform,用来找到两个三角形之间的仿射变换矩阵,cv2.warpAffine将上个函数获得的矩阵应用于图像。
# Apply affine tranform calculated using srcTri and sdtTri to src and output an image of sizedef applyAffineTransform(src, srcTri, dstTri, size):
# Given a pair of triangles,find the affine transform.warpMat = cv2.getAffineTransform(np.float32(srcTri), np.float32(dstTri))
# Apply the Affine Transform just foundto the src image
dst = cv2.warpAffine(src, warpMat, (size[0], size[1]), None, flags=cv2.INTER_LINEAR,
borderMode=cv2.BORDER_REFLECT_101)
return dst
2.3 图像融合
将人脸剖分成一个个小三角形并仿射变换到既定的位置后,进行图片融合。简单来说,通过把图像设置为不同的透明度,把两张图像融合为一张图像(一般要求图像需要是等尺寸大小的),公式如下图所示:

仿射变换时,我们将人脸A的三角形A,人脸B的三角形B仿射到三角形C上。如果不处理,三角形A和三角形B仿射后的图像会叠加在C上。这里我们设置一个透明度参数alpha为0.5,两张人脸各占一半。
imgRect = (1.0 - alpha) * warpImage1 + alpha * warpImage2 warpImage1,warpImage2为经过仿射变换的图像。最后一步,最后将用于遮蔽三角形外的所有像素mask与上个步骤输出的图片结果相乘就可以得到对应区域的值了。 得到融合后的人脸后,最后一步,就是将融合后的人脸交换到待交换的人脸上。
3 人脸交换
人脸交换分为五个步骤:特征点检测,查找凸包,基于凸包三角剖分,仿射变换,无缝克隆。特征点检测,三角剖分和仿射变换之前的部分提及到,所以详细介绍一下查找凸包和无缝克隆。
3.1 凸包算法
如下图所示,所给平面上有点集V,包含p0到p12一共13个点,过p0,p1,p3,p10,p13点作一个多边形,点集V中所有点都包含在形成的这个多边形上。如果当这个多边形是凸多边形的时候,我们就叫它“凸包”。简单来说,点集的凸包即一个最小的凸多边形使得点集中所有的点在该凸边形内或该凸边形上。
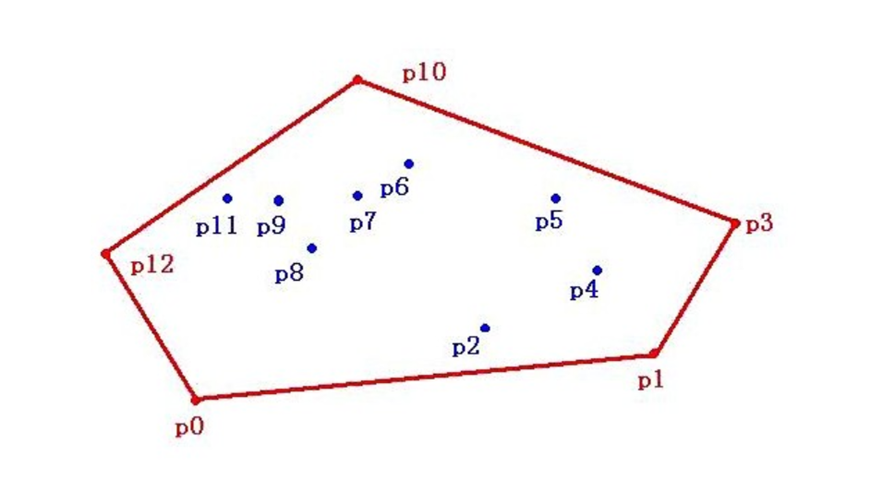
凸包算法为什么会用在人脸交换中呢?人脸交换同样需要特征点检测,同样需要三角剖分,与人脸融合不同的是人脸交换是直接通过仿射变换将人脸A剖分后的三角形仿射到人脸B上。人脸融合剖分的三角形越多,融合效果越完美。 人脸交换不同于融合,第一步只需要将人脸A贴到人脸B上,所以只需要求出68个特征点的凸包多边形,对这个多边形剖分即可。OpenCV便提供了求得这个凸包的函数cv2.convexHull()。人脸交换不同于融合,第一步只需要将人脸A贴到人脸B上,所以只需要求出68个特征点的凸包多边形,对这个多边形剖分即可, 仿射换脸核心代码如下:
# Warps and alpha blends triangular regions from img1 and img2 to imgdef warpTriangle(img1, img2, t1, t2):
# Find bounding rectangle for each triangle r1 = cv2.boundingRect(np.float32([t1])) r2 = cv2.boundingRect(np.float32([t2]))
# Offset points by left top corner of the respective rectangles t1Rect = [] t2Rect = [] t2RectInt = [] for i in range(0, 3): t1Rect.append(((t1[i][0] - r1[0]), (t1[i][1] - r1[1]))) t2Rect.append(((t2[i][0] - r2[0]), (t2[i][1] - r2[1]))) t2RectInt.append(((t2[i][0] - r2[0]), (t2[i][1] - r2[1])))
# Get mask by filling triangle mask = np.zeros((r2[3], r2[2], 3), dtype=np.float32) cv2.fillConvexPoly(mask, np.int32(t2RectInt), (1.0, 1.0, 1.0), 16, 0);
# Apply warpImage to small rectangular patches img1Rect = img1[r1[1]:r1[1] + r1[3], r1[0]:r1[0] + r1[2]]
# img2Rect = np.zeros((r2[3], r2[2]), dtype = img1Rect.dtype) size = (r2[2], r2[3]) img2Rect = applyAffineTransform(img1Rect, t1Rect, t2Rect, size) img2Rect = img2Rect * mask
# Copy triangular region of the rectangular patch to the output image img2[r2[1]:r2[1] + r2[3], r2[0]:r2[0] + r2[2]] = img2[r2[1]:r2[1] + r2[3], r2[0]:r2[0] + r2[2]] * ( (1.0, 1.0, 1.0) - mask) img2[r2[1]:r2[1] + r2[3],
r2[0]:r2[0] + r2[2]] = img2[r2[1]:r2[1] + r2[3], r2[0]:r2[0] + r2[2]] + img2Rect 得到的结果,可以明显看出肤色的差异。
3.2 无缝融合
优秀的技术就像魔法。优秀的魔术师将物理学、心理学和古老的魔术相结合实现了图像的无缝融合。图像的编辑包括全局变化和局部变化,无缝融合是将我们所选中的局部区域无缝且无影响地融合到目标图像中。传统上的工具来完成局部的剪切与融合,是通过克隆工具直接覆盖那部分融合区域的内容,因此如果选择的区域色彩和明暗有明显的差异,会导致明显的边缝,显得突兀。无缝融合由此诞生。 无缝融合的基本原理基于人的生物学特性,我们人眼天生就对“突变”更为敏感。简单来说,比如突然从密闭的黑暗房间出来,我们人眼会受到光线的刺激。但是如果我们渐变的适应一下,就不会感受到光线的刺激。就像白纸上的黑色图形,我们会感觉很“突兀”。同理如果连续平滑的将这个图像由白入灰再变黑,那么我们就感受不到这种突兀。无缝融合就是基于此生物学特性的魔法,虽然是将一张图像融合到另一张图像上,但是我们丝毫感觉不出“突兀”。 这种无缝编辑和克隆方法的核心是数学工具―泊松方程,前提是需满足在所选区域未知函数的拉普拉斯条件和它的Dirichlct边界条件:未知函数的边界值与目标图像中所选区域的边界值相同。因为在这两个条件下方程的解是唯一的。
首先,心理学家Land和Mccan在1971年提出通过拉普拉斯算子的限制可以减缓渐变的梯度,当把一幅图像混淆到另一幅图像上几乎注意不到有什么影响。并且,泊松方程可以完成无缝地填满目标图像中的选中区域。在数学上说到底就是构建方程组:Ax=b。然后通过求解这个方程组以得到每个像素点的值。矩阵A是一个系数矩阵,矩阵的每一行有五个非零元素,对应于拉普拉斯算法的卷积核,而算法的关键在于怎么构建方程组的b值 。首先,计算待融合图像A和背景图像B的梯度场;然后计算融合图像的梯度场,计算完后将A的梯度场覆盖到B的梯度场上;最后对梯度求偏导求得融合图像的散度b,解系数方程Ax=b。虽然看起来涉及到许多数学知识,实际上实现起来只要一个函数cv2.seamlessClone,这就是OpenCV(Computer Vision)。 当然了,如果交换的人脸周围是黑的,就比如下图我们融合得到的中间的人脸,人脸交换时人脸轮廓难免会包括周围的黑色背景。所以,为了使无缝融合取得更好的效果,最好在图片周围加八个点,将环境也粗略融合一下,这样就可以避免人脸周围黑色造成换脸后的“伤疤”。 新加的这8个点,可以通过:
sp = img1.shape # [高|宽|像素值由三种原色构成] #高宽色素 获取图片的高和宽,例如高的一半可以sp[0]/2表示,宽的一半sp[1]/2。 将这张人脸进行人脸交换,可以有效防止周围黑色环境无缝融合产生的“伤疤”。
4 实验分析总结
从第一张图来看,我们对两张性格相同的人脸进行融合,实验结果显示本文提出的人脸融合技术可以实现人脸融合,且最后的融合结果具有高度的真实感,我们基本分辨不出这是融合的效果,初步达到了我们对人脸融合实现的要求。 从第二张、第三张图来看,我们对两张性别不同、肤色不同的人脸进行融合,并分别交换到这两张性别不同的人脸上,从视觉效果上看,我们的算法依然取得了较好的效果,融合的人脸不论是交换在男性身上还是交换在女性身上都显得非常自然,并且肤色也非常自然,性别,肤色并未对算法结果造成影响。
从第四张图来看,我们选择了两张人脸大小不一的图像来进行融合,我们发现融合仍然具有高度的真实感。但是发现一点瑕疵,左边的图像由于灯光的照射使得右侧脸颊有阴影,而我们的算法并不能判断出这是由于灯光产生的阴影还是肤色,导致融合后阴影仍然存在,致使结果有些不自然,但并不影响整个融合的实现,这个问题也是在未来需要解决的。 总的来说,实验结果证明本文提出的人脸融合实现的融合结果具有高度的真实感,基本实现了最初构想,在效果上也达到了预期要求。但仍然还有需要改进的方向: (1)消除灯光照射产生阴影对人脸融合的影响。上述第四张图片由于灯光的照射使得人脸右侧脸颊产生阴影,而我们提到的无缝融合只能将其也归为肤色,导致融合后即使没用光照也有阴影,导致实验效果不自然。方向有两个,一个是对图像进行预处理,消除光照产生的影响;另一个就是在融合过程中对阴影部分进行处理。从可行上来看,对图像进行预处理显得更加便于操作。 (2)消除头发,眼镜等遮挡物对融合的影响。我们的算法是在人脸完全展示的状态下进行剖分并进行融合。如果出现遮挡物,仍然会把遮挡物当成人脸的一部分参与仿射变换并进行融合,这同样会影响实验结果。而随着社会的发展,发型遮挡人脸或者饰品遮挡人脸的情况也比较常见。
编辑:黄飞
 电子发烧友App
电子发烧友App




















评论