提供远超GPS和LTE精度的定位服务,5G、车联网成毫米波关键应用场景

最近一段时间对毫米波通信的研究来看，最为关键的技术是混合模数波束成型（Hybrid Analog-Digital Beamforming，HAD-BF）。至少在学术研究中，目前的毫米波massive MIMO系统已经很少能够脱离HAD架构来进行讨论了。下面简单介绍一下这项技术。

首先要明确的一点是，5G频段目前分成两个部分，一个是sub-6GHz，一个是毫米波。为什么5G要上毫米波频段，主要有两点原因：

1）sub-6GHz已经十分拥挤，各类电子设备互干扰严重。而毫米波频段相对比较“干净”；

2）相比sub-6GHz，毫米波频段能提供更大的信号带宽，而根据香农公式，带宽越大信道容量越大，可支持的通信速率就越高。此外，毫米波还将被应用于5G车联网(V2X)，提供远超GPS和LTE精度的定位服务。这是因为距离分辨率与信号带宽成反比，毫米波的大带宽因而可以达到厘米级的定位精度。

然而，天下没有免费的午餐，毫米波带来了以上诸多好处，当然也有不少的缺陷。其中最大的缺陷就是毫米波的路损(path-loss)和雨衰(rain-attenuation)。众所周知，信号在空间中传播受到的衰减与频率的平方成正比，因此，毫米波信号承受的衰减将是sub-6GHz信号的几十甚至上百倍（注意，这里还是最理想的自由空间损耗情况）。此外，相比于10GHz以下的信号，雨，雪，冰雹等恶劣天气对毫米波的衰减也更为显著。简而言之，毫米波“传不远”。这对于毫米波在5G通信中的实际应用无疑是一个极大的挑战。

那么，如何才能让毫米波信号从基站传播的更远？答案就是利用5G的另一项关键技术massive MIMO，国内翻译成大规模MIMO或者大规模天线阵列。由于天线尺寸与信号波长成正比，massive MIMO天线阵列可以很容易地布置在毫米波系统中而不占用太大的空间。在massive MIMO阵列下，我们可以在空间中将信号能量集中在极窄的波束精确地指向下行用户，从而最大化在该方向的传播距离。

有多窄？可以放如下一张仿真图给大家一个直观印象。下图是一个利用了HAD结构的简单的128天线的massive MIMO基站的波束图样(Beampattern)，我们对8个角度的用户形成8个窄波束。大家可以看到，图中-30~0度区域，彼此十分靠近的几个用户也能够被精确地区分出来。

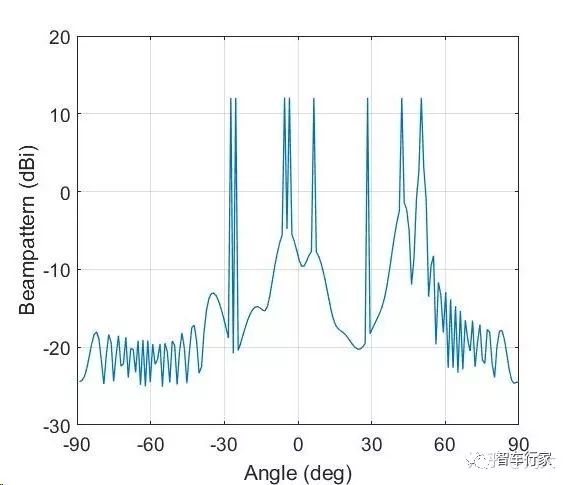
Massive MIMO虽然解决了毫米波传播距离的问题，但是又带来了新的问题，那就是昂贵的造价和高功耗。在普通MIMO系统中，每根天线后面都会接一个独立的RF Chain，其中包括了放大器，混频器，滤波器和ADC/DAC等器件。

当工作频段较低时，这些器件的成本和功耗尚可接受。但在毫米波频段，这些器件的成本较高，并且还要乘以大规模天线/RF Chain的数量，这就导致了完全不可接受的造价和功耗。这无疑又是一个巨大的挑战。怎么解决这一问题呢，一个自然的思路就是减少RF Chain的数量，但是为了形成窄波束，还是需要保留大规模天线阵列，每个RF Chain则通过多个移相器(Phase Shifter, PS)连接多个天线。这事实上借鉴了相控阵雷达的理念。

典型的相控阵雷达模型只有一个RF Chain，但是通过移相器连接了成百上千个天线阵元，如此一来，其发射出去的信号就是一个benchmark信号的多个移相版本在空间中的叠加，从而可以指向特定的方向。相比于完整的RF Chain，移相器的成本要便宜许多，功耗也要低得多。

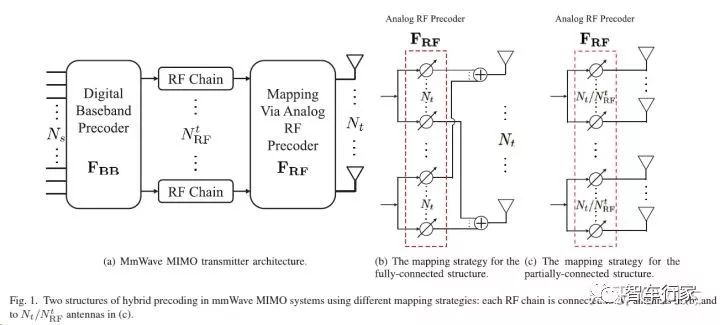
习惯上，我们把移相称作是模拟处理，把同时调整信号幅度和相位称作是数字处理（这是学界约定俗成的习惯，与狭义的模拟和数字信号处理有所不同），因此这一新的结构就被称为混合模数(HAD)结构。我们来看以下示意图，分别给出了两种HAD结构。如图(a)所示， 个数据流通过一个数字预编码矩阵 传输到 个RF Chain上，再通过移相器网络矩阵 映射到 根天线上发射出去。图(b)的结构叫做完全连接结构(Fully-connected, FC)，即，每一个RF Chain通过到 个移相器与所有天线相连接。

图(c)则成为部分连接结构(Partially-connected, PC), 即，每个RF Chain通过 个移相器连接 根天线，从而构成一个子阵列(sub-array)。显然，后一种结构需要的移相器更少，但性能相对也会更差一些。

接下来的问题是，在HAD结构下，我们如何调整移相器的相位以及如何设计数字预编码矩阵，来使得这套系统与全数字的massive MIMO系统的性能尽量接近呢？这就涉及到矩阵 和 的设计。

在FC结构下，矩阵 的每一个元素对应了一个移相器，因此要求是恒模的，也就是说我们有，其中代表连接第i根天线和第j个RF Chain的移相器。在PC结构下，由于RF Chain和天线之间不是全连接关系，因此矩阵中存在零元素，代表没有连接的RF Chain和天线。

我们以FC结构为例，一个经典的设计方法是求解以下优化问题：

其中 代表最优的全数字预编码矩阵，一般是对信道矩阵做SVD得到。第一个约束条件约束了的元素均为恒模，第二个约束条件约束总发射功率为 。该问题实质上是一个矩阵分解问题。我们希望利用HAD结构来逼近全数字系统的性能。遗憾的是，由于恒模约束的存在，上述问题是非凸的并且NP-hard。这就使得全局最优解难以在多项式时间内求得。一个经常采用的思路是所谓的交替最小化方法(Alternating minimization, AltMin)，即，首先固定，求解 （子问题1），然后固定得到的，来求解（子问题2）。

迭代求解两个子问题直到目标函数收敛。这是所谓的coordinate descent方法，求解每一个子问题都需要保证是下降算法，因此目标函数能够在每一步迭代都下降。容易看到，子问题1是较容易求解的，事实上，一个简单的次优解是求的最小二乘解，然后乘以一个系数来满足功率约束。而由于恒模约束的存在，子问题2的求解则较为复杂。通常可以采用经典的梯度投影算法，即在每一步梯度下降后将得到的点的每一个元素归一化为恒模。

另外一种性能更好的算法是所谓的流形优化算法(Manifold Optimization)，其思想较为复杂，这里不再赘述。另外值得一提的是，对于PC结构，由于中存在零元素，以上问题的求解可以大大简化，甚至可以得到子问题2的最优闭式解，因此采用PC结构有极低的设计复杂度。

以上是利用优化算法来进行HAD结构的设计。然而由于实时性的要求，我们很难将以上算法应用到实际系统中。因此，一种更为简单的思路是利用毫米波通信系统的信道结构。

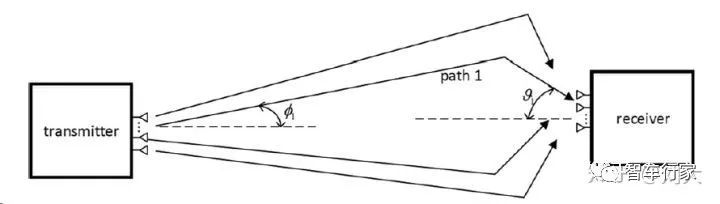
我们来看上图中的点对点毫米波信道。与低频信道不同，由于毫米波基本沿直线传播，绕射能力差，其信道的散射路径较少，往往远少于发射和接收天线的数量，因此其信道模型具有丰富的几何特征。

而低频信道由于散射路径丰富，往往建模成随机信道比如瑞利分布，因此并不包含通信环境的信息。利用经典的S-V信道模型，一个具有 根发射天线， 根接收天线，以及 条散射路径的归一化窄带毫米波信道可以写成

假设发射接收均为均匀线性阵列(Uniform Linear Array)，则

是N维天线阵列的方向矢量(steering vector)，又称为array response。而 和 则分别代表第 条路径的到达角(Angle of Arrival, AoA)和出发角(Angle of Departure, AoD)，一般认为在 均匀分布。 则代表第 条路径的路损和相移，一般建模为高斯分布。根据以上模型，一个简单的思路是，发射端形成个发射波束指向 个AoD，接收端则形成个接收波束指向 个AoA，就可以与信号的传播路径完全重合，从而在信号传播的方向上最大化发射与接收功率。

这里我们可以直接采用模拟波束成型，即令的每一列为对应方向的方向矢量的共轭。注意到这里我们仅需激活 个RF Chain，令每个RF Chain对应的移相器阵列指向一个AoD即可。则仅需要对每个波束进行简单的功率分配。为了对齐AoD和AoA，发射端和接收端还需要进行beam training，其实质是找到信噪比最佳的发射和接收波束。

如果信道中的散射体在移动，则还需要跟踪AoD和AoA的变化，这就是所谓的beam tracking，也可以理解为具有一定先验信息的beam training。这两者也是毫米波系统中的经典问题，都需要利用HAD架构来实现。

最后一个问题是实际系统中移相器总是离散取值的，我们不可能对信号进行任意大小的移相。因此需要在以上方案里引入离散的相位码本(Codebook)。这些码本中的码字对应了空间中离散的AoA和AoD取值，因此涉及到一些离散优化问题，有兴趣的知友可参考HAD方案的提出者Robert Heath教授的论文。

我们总结HAD方案的提出，可以看到这是一个环环相扣的过程。首先是为了解决毫米波的路损和雨衰问题需要大规模MIMO阵列，而为了降低毫米波大规模MIMO的成本和功耗需要减少RF Chain的数量，并用移相器来进行代替，得到了HAD结构，为了使得HAD系统的性能尽量接近全数字系统，又要对移相器的相位进行精心设计，这就衍生出了多种设计方法。

以我有限的学术经验来看，这是一个非常典型的从实际工程需求出发上升到理论研究，最后又能落地到实际工程中的科研范式。作为工科研究人员，我心中最理想的研究就是既能飘到天上，又能落回地下，这些在HAD方案中都得到了完美的体现。