简要分享10种电路分析方法

分析电路的10大方法

电路：由金属导线和电气、电子部件组成的导电回路，称为电路。在电路输入端加上电源使输入端产生电势差，电路连通时即可工作。

电流的存在可以通过一些仪器测试出来，如电压表或电流表偏转、灯泡发光等；按照流过的电流性质，一般把它分为两种：直流电通过的电路称为“直流电路”，交流电通过的电路称为“交流电路”。

电路问题计算的先决条件是正确识别电路，搞清楚各部分之间的连接关系。对较复杂的电路应先将原电路简化为等效电路，以便分析和计算。识别分析电路的方法很多，现结合具体实例介绍十种方法。

01特征识别法

串并联电路的特征是；串联电路中电流不分叉，各点电势逐次降低，并联电路中电流分叉，各支路两端分别是等电势，两端之间等电压。根据串并联电路的特征识别电路是简化电路的一种最基本的方法。

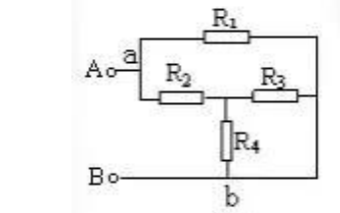
例1．试画出图1所示的等效电路

解析：解：设电流由A端流入，在a点分叉，b点汇合，由B端流出。支路a—R1—b和a—R2—R3(R4)—b各点电势逐次降低，两条支路的a、b两点之间电压相等，故知R3和R4并联后与R2串联，再与R1并联，等效电路如图2所示。

02

伸缩翻转法

在实验室接电路时常常可以这样操作，无阻导线可以延长或缩短，也可以翻过来转过去，或将一支路翻到别处，翻转时支路的两端保持不动；

导线也可以从其所在节点上沿其它导线滑动，但不能越过元件。这样就提供了简化电路的一种方法，我们把这种方法称为伸缩翻转法。

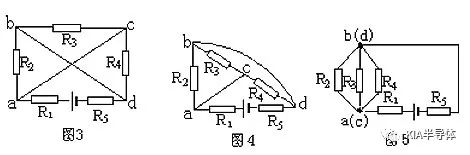
例2．画出图3的等效电路

解析：解：先将连接a、c节点的导线缩短，并把连接b、d节点的导线伸长翻转到R3—C—R4支路外边去，如图4。

再把连接a、C节点的导线缩成一点，把连接b、d节点的导线也缩成一点，并把R5连到节点d的导线伸长线上(图5)。由此可看出R2、R3与R4并联，再与R1和R5串联，接到电源上。

03

电流走向法

电流是分析电路的核心。从电源正极出发(无源电路可假设电流由一端流入另一端流出)顺着电流的走向，经各电阻绕外电路巡行一周至电源的负极，凡是电流无分叉地依次流过的电阻均为串联，凡是电流有分叉地分别流过的电阻均为并联。

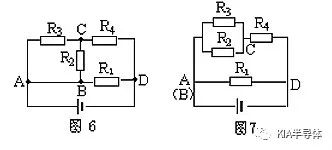
例3．试画出图6所示的等效电路

解：电流从电源正极流出过A点分为三路(AB导线可缩为一点)，经外电路巡行一周，由D点流入电源负极。第一路经R1直达D点，第二路经R2到达C点，第三路经R3也到达C点，显然R2和R3接联在AC两点之间为并联。

二、三络电流同汇于c点经R4到达D点，可知R2、R3并联后与R4串联，再与R1并联，如图7所示。

04

等电势法

在较复杂的电路中往往能找到电势相等的点，把所有电势相等的点归结为一点，或画在一条线段上。当两等势点之间有非电源元件时，可将之去掉不考虑；当某条支路既无电源又无电流时，可取消这一支路。我们将这种简比电路的方法称为等电势法。

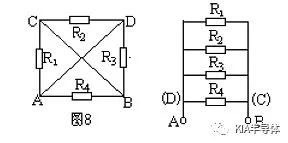
例4．如图8所示，已知R1=R2=R3=R4=2Ω，求A、B两点间的总电阻。

解析：设想把A、B两点分别接到电源的正负极上进行分析，A、D两点电势相等，B、C两点电势也相等，分别画成两条线段。电阻R1接在A、C两点，也即接在A、B两点；

R2接在C、D两点，也即接在B、A两点；R3接在D、B两点，也即接在A、B两点，R4也接在A、B两点，可见四个电阻都接在A、B两点之间均为并联(图9)。所以，PAB=3Ω。

05

支路节点法

节点就是电路中几条支路的汇合点。所谓支路节点法就是将各节点编号(约定；电源正极为第1节点，从电源正极到负极，按先后次序经过的节点分别为1、2、3……)，从第1节点开始的支路，向电源负极画。

可能有多条支路(规定：不同支路不能重复通过同一电阻)能达到电源负极，画的原则是先画节点数少的支路，再画节点数多的支路。然后照此原则，画出第2节点开始的支路。余次类推，最后将剩余的电阻按其两端的位置补画出来。

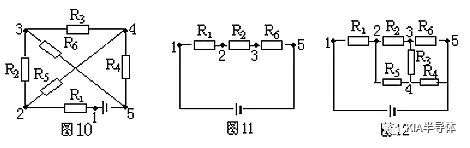
例5．画出图10所示的等效电路。

解析：图10中有1、2、3、4、5五个节点，按照支路节点法原则，从电源正极(第1节点)出来，节点数少的支路有两条：R1、R2、R5支路和R1、R5、R4支路。取其中一条R1、R2、R5支路，画出如图11。

再由第2节点开始，有两条支路可达负极，一条是R5、R4，节点数是3，另一条是R5、R3、R5，节点数是4，且已有R6重复不可取。所以应再画出R5、R4支路，最后把剩余电阻R3画出，如图12所示。

06

几何变形法

几何变形法就是根据电路中的导线可以任意伸长、缩短、旋转或平移等特点，将给定的电路进行几何变形，进一步确定电路元件的连接关系，画出等效电路图。

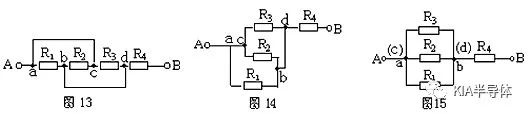
例6．画出图13的等效电路

解析：使ac支路的导线缩短，电路进行几何变形可得图14，再使ac缩为一点，bd也缩为一点，明显地看出R1、R2和R5三者为并联，再与R4串联(图15)。

07

撤去电阻法

根据串并联电路特点知，在串联电路中，撤去任何一个电阻，其它电阻无电流通过，则这些电阻是串联连接；在并联电路中，撤去任何一个电阻，其它电阻仍有电流通过，则这些电阻是并联连接。

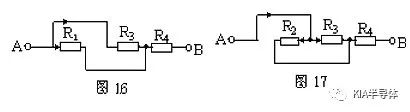
解析：仍以图13为例，设电流由A端流入，B端流出，先撤去R2，由图16可知R1、R3有电流通过。再撤去电阻R1，由图17可知R2、R3仍有电流通过。同理撤去电阻R3时，R1、R2也有电流通过由并联电路的特点可知，R1、R2和R3并联，再与R4串联。

08

独立支路法

让电流从电源正极流出，在不重复经过同一元件的原则下，看其中有几条路流回电源的负极，则有几条独立支路。未包含在独立支路内的剩余电阻按其两端的位置补上。应用这种方法时，选取独立支路要将导线包含进去。

方案一：选取A—R2—R3—C—B为一条独立支路，A—R1—R5—B为另一条独立支路，剩余电阻R4接在D、C之间，如图19所示。

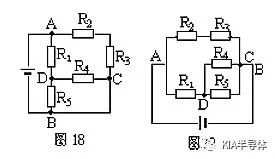
例7．画出图18的等效电路。

方案二：选取A—R1—D—R4—C—B为一条独立支路，再分别安排R2、R3和R5，的位置，构成等效电路图20。

方案三：选取A—R2—R3—C—R4—D—R5—B为一条独立支路，再把R1接到AD之间，导线接在C、B之间，如图21所示，结果仍无法直观判断电阻的串并联关系，所以选取独立支路时一定要将无阻导线包含进去。

09

节点跨接法

将已知电路中各节点编号，按电势由高到低的顺序依次用1、2、3……数码标出来(接于电源正极的节点电势最高，接于电源负极的节点电势最低，等电势的节点用同一数码，并合并为一点)。然后按电势的高低将各节点重新排布，再将各元件跨接到相对应的两节点之间，即可画出等效电路。

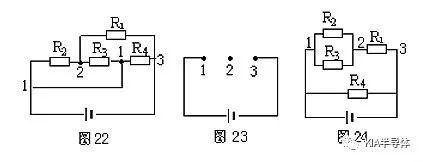
例8．画出图22所示的等效电路。

解析：节点编号：如图22中所示。

节点排列：将1、23节点依次间隔地排列在一条直线上，如图23。

元件归位：对照图22，将R1、R2、R3、R4分别跨接在排列好的1、2得等效电路如图24。

10

电表摘补法

若复杂的电路接有电表，在不计电流表A和电压表V的内阻影响时，由于电流表内阻为零，可摘去用一根无阻导线代替；由于电压表内阻极大，可摘去视为开路。用上述方法画出等效电 搞清连接关系后，再把电表补到电路对应的位置上。

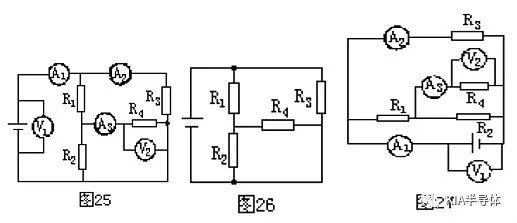
例9．如图25的电路中，电表内阻的影响忽略不计，试画出它的等效电路。

解析：先将电流表去，用一根导线代摘替，再摘去电压表视为开路，得图26。然后根据图25把电流表和电压表补接到电路中的对应位置上，如图27所示。