关于从指定方向图合成阵列优化工作流程的分析

在那些使用传感器阵列的应用中，例如 WLAN、LTE 和 5G 无线通信系统、相控阵雷达和声信号波束成形系统，设计通常从满足某些性能标准的阵列方向图开始。这些标准包括诸如主瓣方向性和宽度、零位置和旁瓣电平之类的参数。

由于阵列通常包含数百甚至数千个阵元，因此可能需要多次迭代才能在产生期望方向上收敛到一个所需的方向图。迭代需要时间，并且当需要考虑多个参数时难以彻底完成。

优化技术可以极大地提高阵列分析过程的效率。您可以通过一系列权重和阵元位置来评估一种方向图，并且可以通过自动过程的每次迭代来评估已生成的方向图与期望方向图之间的差异。

本文介绍了一种工作流程，使用 Phased Array System Toolbox、Optimization Toolbox 和 Global Optimization Toolbox 的优化技术来提供解决方案。

设计选项和约束

为确保解决方案满足设计指标，我们必须了解设计选项和优化过程中需要考虑的约束条件。

影响阵列形式的参数包括阵列中阵元的数量、阵元的晶格结构和阵列形式。在阵列内，与每个阵元相关联的参数还确定了波束方向图特征，包括应用于每个阵元（幅度或相位）的权重和阵元在阵列内的位置。这些参数可以用作“控制旋钮”，满足您想要的性能目标。

对于多元阵列，设计的自由度将根据最终应用的成本和复杂性而变化。例如，在最基本的系统中，仅幅度权重可用。然而，许多架构支持阵元或子阵列的复数加权，可提供幅度和相位控制。通过这种类型的架构，波束可以通过电子方式转向和成形（图 1）。

图1：灵活的相控阵架构。

设计中的阵列形式通常由终端系统形状因子的约束驱动，但各阵元之间的间距可以是灵活的。然而，这种灵活性通常受到实际制造条件的限制。例如，各阵元不能太靠近，否则将影响阵列的有效性。

为了说明如何将这些选项和约束纳入优化工作流程，我们将提供两个示例。在第一个示例中，我们使用具有均匀间距的 8 阵元线阵来生成一组阵元权重，重点是匹配已知方向图。在第二个示例中，我们构建了一个面阵，其中阵元权重和阵元位置收敛，以实现一组阵列性能指标。也就是说，我们从权重扩展到阵元位置，展示如何通过将约束条件置于优化问题中，来塑造方向图以满足要求。

示例 1：仅优化权重

在这个例子中，我们将完成以下步骤（图 2）：

确定期望方向图

开发一个代价函数，尽可能缩小起始方向图和期望方向图之间的距离

运行优化

使用生成的权重查看方向图，并将其与期望方向图进行比较

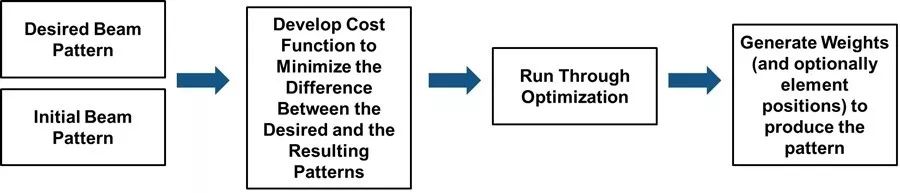
图2：示例 1 的工作流程步骤。

我们从期望的 2D 方向图 Beam_d 开始，该方向图具有一组特定的方位角和仰角。然后构建一个成本函数，缩小期望方向图 Beam_d 与加权向量 weight_o 生成的方向图之间的距离。优化的初始条件基于均匀加权。此方向图包含在以下代码的目标函数中。

因为我们正在尝试确定可以缩小两个波束方向图之间距离的阵元权重，所以我们将使用 Optimization Toolbox 的 fmincon 函数，该函数包含目标函数、权重的初始值和约束。初始加权值设置为 1。约束是分数加权值的最小值和最大值，我们将其定义为介于 0 和 1 之间。

当我们调用 fmincon 时，我们提供了目标函数的句柄，它可以区分一开始使用的方向图与迭代细化权重时生成的方向图。优化结束时，我们可以得到一组权重，将其应用于数组阵元时会与期望方向图匹配。图 3 中的曲线显示了方位角上期望方向图和合成方向图的幅度。

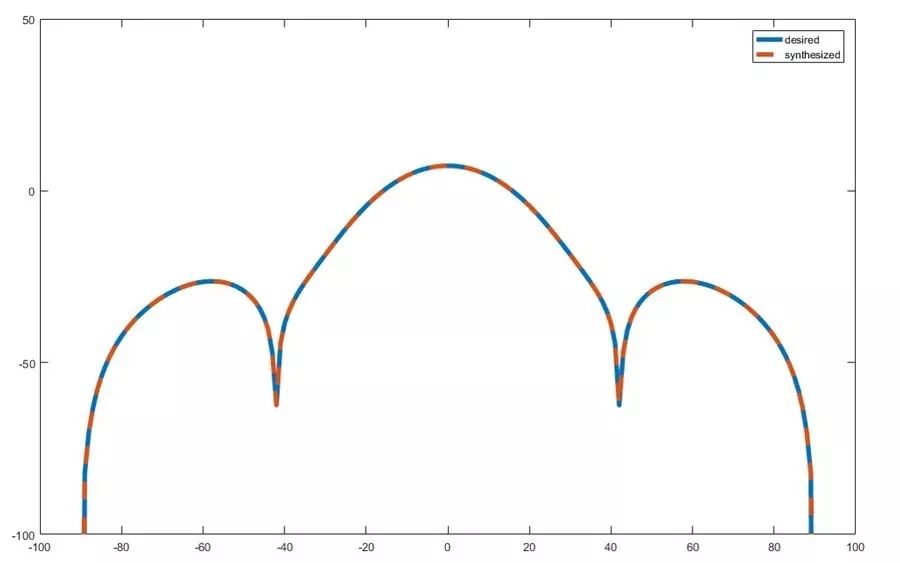
图3：优化后期望方向图和合成方向图的比较。

示例2：优化权重和阵元位置

在此示例中，我们将完成以下步骤（图 4）：

识别方向图属性

定义约束，确保系统可以实现

开发一个客观（成本）函数，得到所需“方向”的方向图属性

运行优化

将优化的方向图与期望方向图进行比较

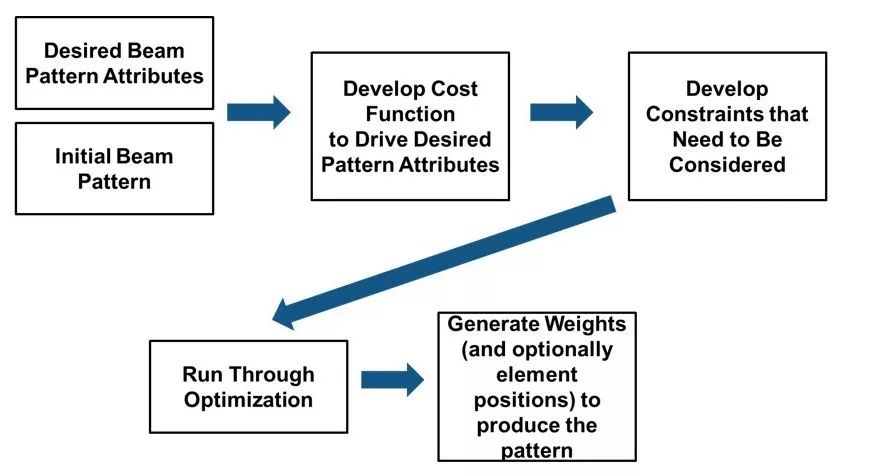
图4：示例 2 的工作流程步骤。

请注意，与示例 1 只控制阵元的幅度权重不同，这种设计更复杂，具有更多的阵列阵元。我们现在要控制每个阵元的幅度、相位和 2D 位置。我们的优化目标是降低方向图的最大旁瓣电平。

由于此示例具有许多局部最优解且目标非光滑，因此我们将使用 Global Optimization Toolbox 的 patternsearch 求解器。当目标光滑时，globalsearch 可能是更好的选择。

与前面的示例一样，我们需要确保优化过程计算出的阵元位置间隔不会过于紧密。我们将为幅度和相位设置相同的最小和最大范围。

在此示例中，我们的自由度为 100：除了 25 个幅度值和 25 个相位值（每个阵元一个）之外，还有 50 个 y-z 位置来描述 25 个阵元位置。每个参数的下限（lb）和上限（ub）值包含在 100 个阵元的 MATLAB 向量中，其中向量元素 1 至 25 表示（yz 阵列的）初始 y 位置，而向量元素 26 至 50 表示初始 z 位置。

图 5 左侧的阵列显示了间隔均匀的阵元的初始位置。对于 y-z 平面阵元位置的下限和上限，我们使用（±0.24 * λ）均匀矩形阵列起点的间距建立网格（图5，右）。

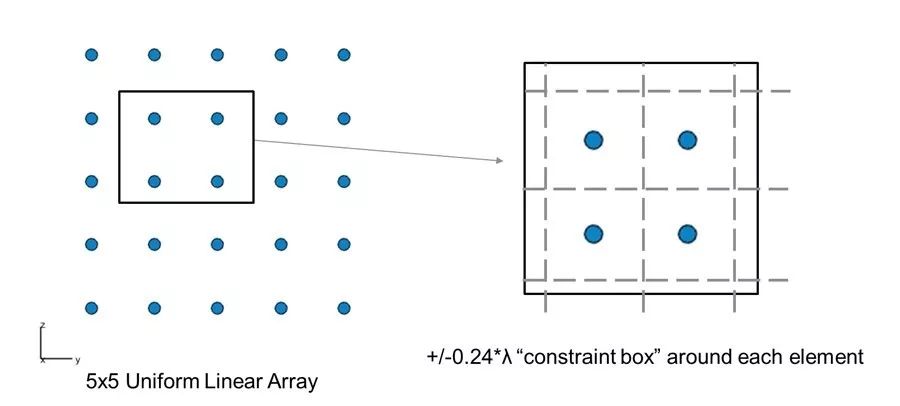
图5：左图：均匀线性阵列（5x5个阵元）。右图：每个阵元周围对应的“约束框”。

向量元素 51 至 75 表示初始幅度值，向量元素 76 至 100 表示初始相位值。该向量的每个部分包括 25 个参数，对应 5x5 阵列大小。

我们首先使用 Phased Array System Toolbox 建立一个 5x5 阵列，从均匀间隔的阵元开始。然后，我们使用 ConformalArray 构造来更改每个阵元的位置。我们可以随着整个优化过程中位置的变化更新我们的模型。

请注意，我们在此阵列模型中使用了理想的余弦天线阵元。我们也可以使用 Antenna Toolbox 中的方向图或外部测量的方向图。

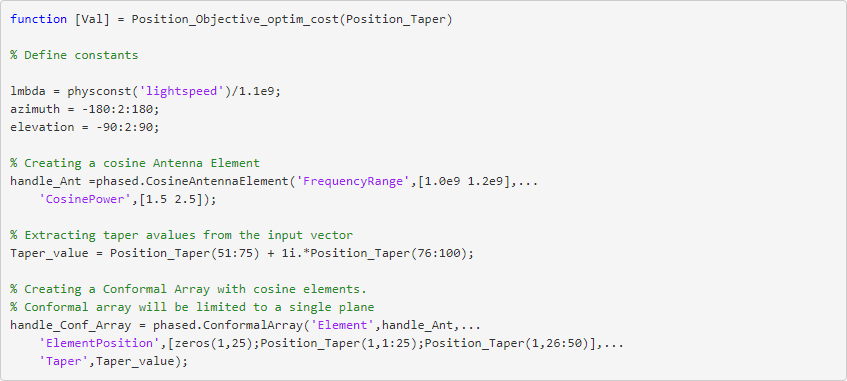
建立了阵列后，我们就可以确定方位角和仰角的波束方向图。然后，我们可以使用此数据来提取与方向图相关的关键指标。我们将重点关注旁瓣，但也可以考虑许多其他参数，例如主瓣增益或 3dB 波瓣宽度。

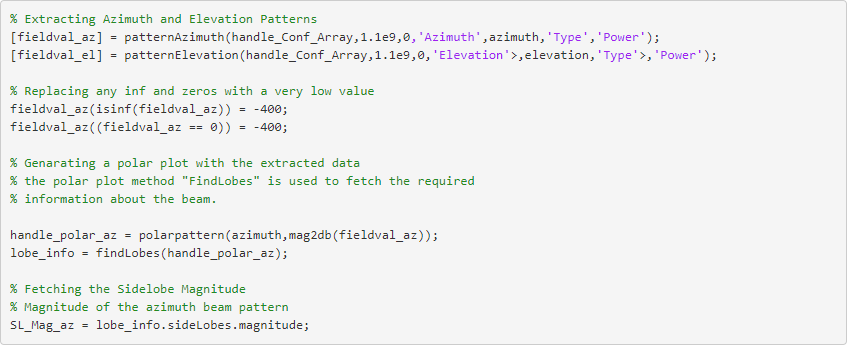
建立目标函数

设置优化参数，实现 5x5 平面阵列的方位角和仰角的性能。构建方向图，减少旁瓣电平的幅度。其他类似的例子可能包括增加主瓣的幅度或减小 3dB 带宽。

在随后的代码中，我们使用方位角和仰角旁瓣的总和。我们还增加了一个方位角和仰角旁瓣电平之间的绝对差值，以确保它们达到峰值时是接近的。因为优化引擎可以最小化目标函数，所以每次迭代此函数时，Val 都为最小值。您可根据特定要求调整这些参数。

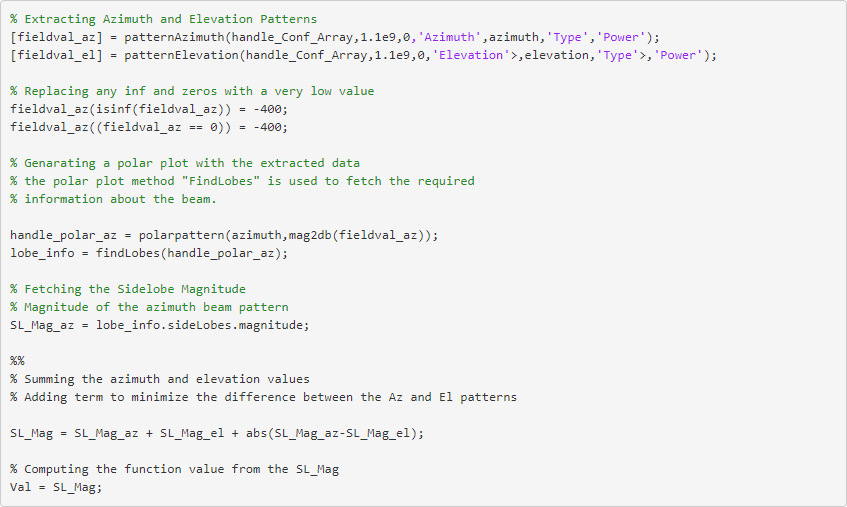
图 6 显示了所得到的方位面中的极坐标图。

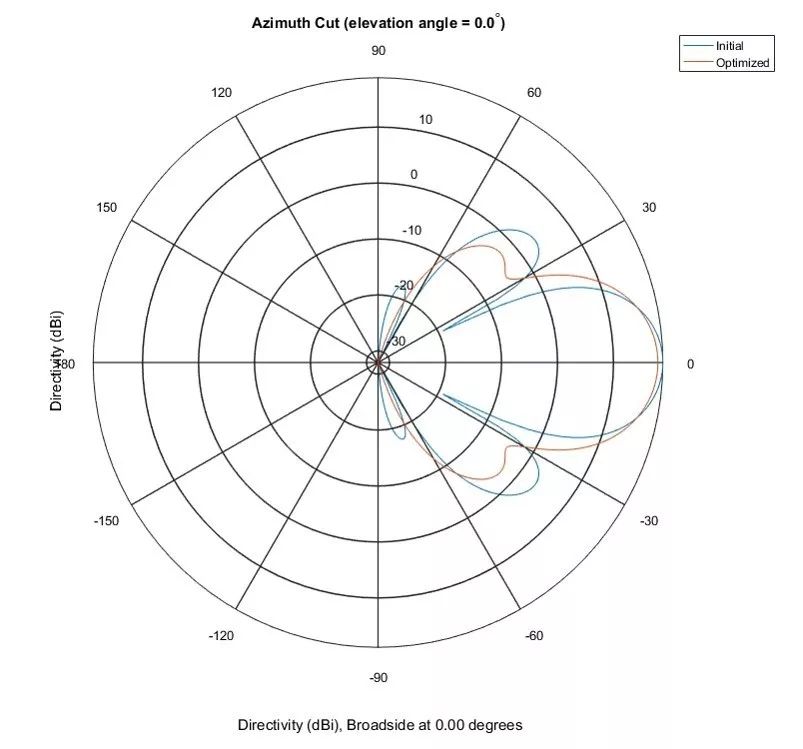
图6：方位面中的极坐标图案显示起点图案（蓝色线）和优化后的图案（橙色线）。

图 7 显示了仰角面的相应视图。

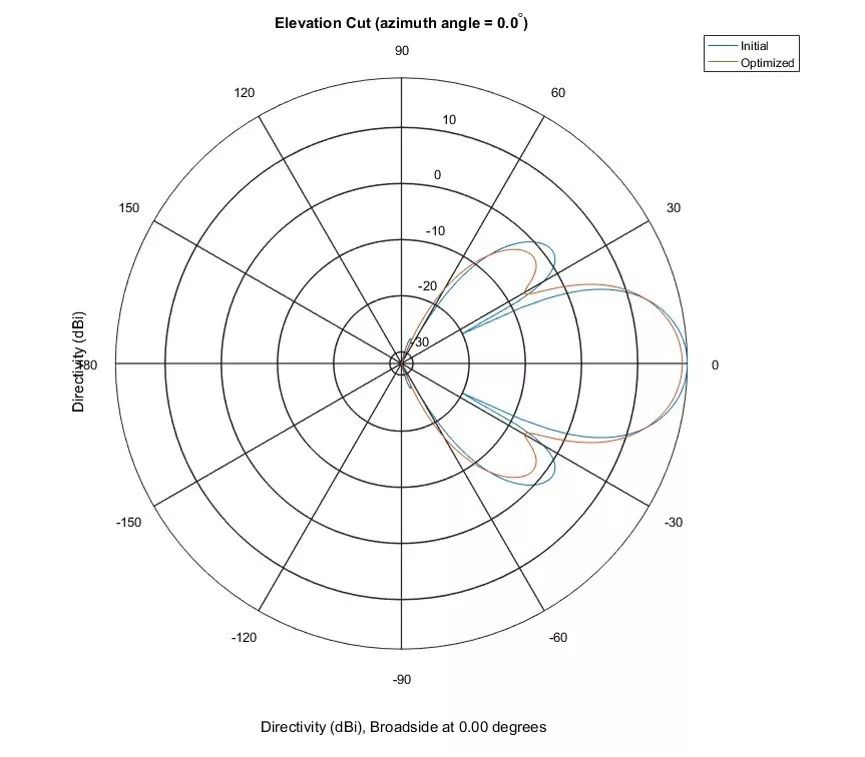
图7：仰角面中的极坐标图案显示起点图案（蓝色线）和优化后的图案（橙色线）。

使用通过优化函数的多次迭代返回的权重和阵元位置生成新的方向图。图 8 显示了得到的阵元位置和波束方向图。

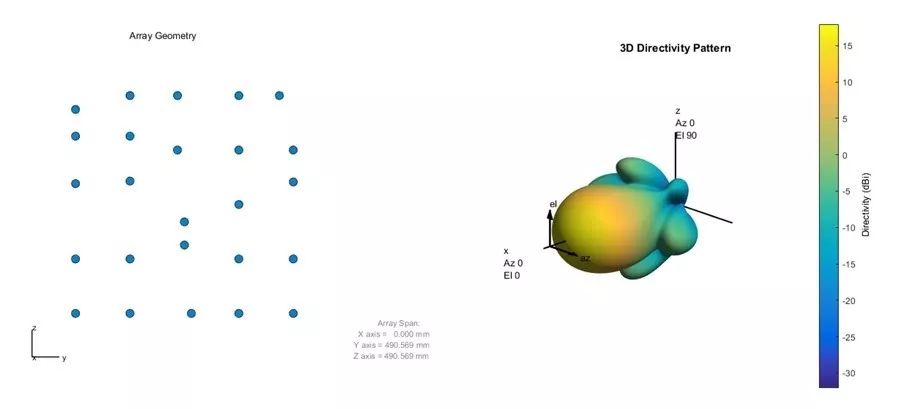
图8：优化后得到的阵列和波束方向图。

扩展示例

在这些示例中，所有分析都在单个频率值下完成。实际上，系统必须在一系列频率上工作。

可以将同样的优化技术应用于各种频率的操作。例如，针对宽带应用，我们可以研究整个频带内等间隔的多个频率。然后决定应用的哪个方面最重要。例如，最好针对特定组合进行优化，并基于该组合选择定位。所有其他场景只需使用加权即可提供“尽力而为”的服务。

如果认为所有频率组合都拥有特定性能要求更重要，则可以相应地调整优化过程。还可以扩展优化过程，在一组导向矢量上构建最佳子阵列架构。

除了扩展优化以覆盖更宽的频率范围外，还可以将相移量化效果添加到 Phased Array System Toolbox 模型中，确保终端系统的行为与仿真结果的相同。这对优化结果的构建来说非常重要。

可以通过优化技术实现期望的波束性能，并以类似的方法设计构建在多个平面上的共形阵列。