如何设计转换映射指导成功的异步状态机

虽然ASIC公司和“良好的工程实践”强调同步设计技术，但时钟速度的增加使用速度高达50至200 MHz，这迫使设计人员实施异步逻辑电路。不幸的是，虽然大多数数字设计工程师都熟悉组合和同步时序逻辑电路，但异步时序逻辑设计的世界仍然模糊不清。过渡地图可以指导设计人员通过这个不熟悉的世界来实现可靠的异步设计。旅程从一些基本概念和定义开始。数字电路可以分为组合电路或顺序电路。组合电路是那些输出值完全取决于输入信号电平的电路。顺序电路的输出值和当前状态值不仅取决于当前输入值，还取决于电路的先前状态。您可以将时序电路分为两种类型：同步和异步。在同步电路中，当前状态在时钟的边沿上变化（图1 a）。异步电路中的当前状态在一个或多个输入变量的转换之后发生变化，然后是电路的传播延迟周期（t pd ）。

图1同步（a）和异步（b）电路的行为设计模型几乎相同。主要区别在于异步电路依赖于传播延迟来达到当前状态值。

创建顺序异步逻辑电路时，请注意电路中的传播延迟。否则，可能发生不希望的输出毛刺或甚至永久的不希望的状态。为避免异步电路的危险，设计人员更多地选择同步实现。然而，同步电路也存在固有问题。设计人员必须将输入信号与状态机时钟同步，以避免亚稳态。此外，输入值的变化仅在同步时钟发生之后影响输出值，增加了电路响应所需的时间（即延迟）。时钟延迟和输入信号同步的需要会严重降低系统的性能。

图1 b是异步顺序状态机的框图模型。该模型由一个组合逻辑块组成，其输出信号决定了下一个状态值。块的输入变量是外部输入信号和当前状态变量。该模型假设组合逻辑没有传播延迟，并且当前状态变量在建立时间之后采用下一状态变量的值。建立时间等于真实组合逻辑块中可能出现的最长传播延迟（t pd ）。

当电路稳定时（定义为在等于或长于t pd 的时间段内保持相同的变量），当前和下一状态变量具有相同的值。然而，有时，状态变量在当前状态和下一状态变量达到稳定状态之前呈现几个中间值。这些中间值表示不稳定状态，其中输出变量值对于给定的输入值组合保持变化。在极端情况下，电路会振荡。

由于通过电路的各种信号路径具有不同的传播延迟，因此两个或多个输入信号的同时变化可能会导致不可预测的状态转换。因此，为了避免不受控制的行为，设计应该一次只允许一个输入变量。此外，连续输入信号变化之间的时间间隔应该比达到稳定状态所需的时间长。当强制执行这些限制时，电路以“基本模式”运行。

电路实现可能允许两个或多个状态变量由于输入信号转换而同时发生变化。这种电路具有竞争条件，电路行为取决于哪个状态变量变化最快。如果在几次临时状态转换后电路达到的稳定状态是相同的，无论哪个状态变量更快，电路都有非关键的比赛。如果最终状态不同，则该赛道有重要的比赛。良好的设计必须在基本模式下运行，避免关键竞争条件。

锁存器保持当前状态值

在同步状态机中，触发器是保存当前状态值的存储器元素。在异步状态机中，存储器单元是锁存器;图2显示了这样的锁存电路。产品术语（A＆amp; B）称为START术语。当该项为真时，输出Z为真。产品项（B＆amp; Z），其中一个输入变量是来自输出的反馈，称为HOLD项。一旦START为真，长于t pd ，只要HOLD项保持为真，输出Z就会保持设置。

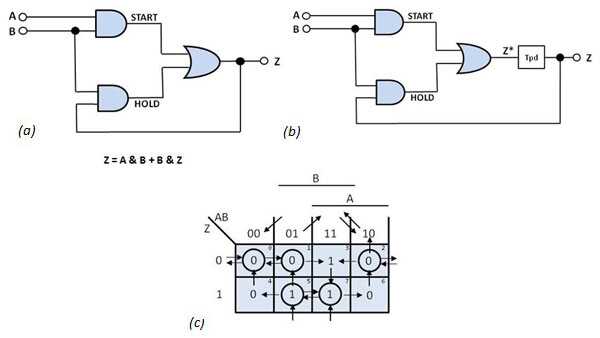
图2锁存电路（a）是异步状态机的存储元件。锁存器的异步模型（b）和转换映射（c）提供了对电路行为的深入了解。

图2 b说明了异步锁存器的模型。假设原始门具有零延迟并且组合电路（Z *）的输出是下一状态变量。输出Z在通过电路等于传播延迟（t pd ）的时间之后取值Z *。下一状态变量Z *可以表示为布尔方程：Z *（t）= A＆amp; B + B＆amp; Z（t）。输出Z（当前状态变量）是Z（t + t pd ）= Z *（t）。除了块延迟之外，该电路模型可以作为组合逻辑进行分析;因此，您可以使用称为转换映射的卡诺图类型来研究其行为。图2 c显示了锁存模型的转换映射。

转换映射的每一列代表外部输入变量的组合，每行代表一个组合现状变量。这些组合被安排成使得相邻的行或列的差异仅在于一个变量的变化。由行和列定义的方块包含电路的相应下一状态值（Z *）。在图2中，因为A和B是外部输入变量而Z是唯一的当前状态变量，所以你需要确定这个锁存器的行为是一个映射四列两行。

此映射包含许多参考标记，有助于理解相应电路的行为。在每个输入变量名称下面有一个水平条，它覆盖变量为true的那些方块。正方形的角落有数字，方便参考。地图顶部列之间的倾斜箭头表示Z-的电平转换 - 如果有的话 - 由于输入转换。

如果将电路的总状态定义为输入和当前状态变量的当前组合，过渡图的每个方格与电路的总状态具有唯一的对应关系。在地图内从正方形移动到正方形对应于电路总状态的变化。当电路到达其下一状态值与其各自的行值一致的方形时，电路已达到稳定状态。过渡图显示了圈出的所有稳定状态。其余的方块表示不稳定状态。

转换映射跟踪电路变化

此时，请注意异步电路的状态几乎在外部输入改变后立即改变，而不是像在同步电路中那样跟随时钟的边沿。在使用转换映射分析异步电路的行为时，请记住，当输入变量发生变化时，电路的状态变化对应于表示新输入组合的列的立即水平过渡。如果下一状态Z *的新值与当前状态Z一致，则新状态是稳定的。否则，垂直转换随后发生，直到电路达到Z * = Z的状态。

分析图2 c中的映射，其中说明这种行为。假设输入和输出变量值分别为AB = 00和Z = 0;然后，square 0表示电路的状态，并给出下一个状态值Z * = 0。由于Z *和Z相同，因此输出保持稳定。如果B变为“1”，则当前状态仍为“0”，尽管方形1表示总状态。如果A现在变为“1”，则下一状态Z *变为“1”并且不再等于Z.电路状态移至平方3.该状态不稳定，迫使锁存器状态垂直移动到稳定状态状态为7，因为AB保持为“11”。以类似的方式，每次输入值改变时分析锁存器的下一个状态。

分析也适用于具有多个状态的电路 - 记忆元素。图3 a显示了一个逻辑图，您可以通过检查图3中相应的布尔方程和卡诺图来推导出span> b 。转换图图3 c，是两个卡诺图的组合，通过连接Z *和Q的相应值形成*。地图顶部的值表示电路输入变量A和B的当前值。地图左侧的值表示电路的当前状态值（ZQ）。稳定状态，正方形具有下一州的价值es与相应的行值重合，用圆圈表示。

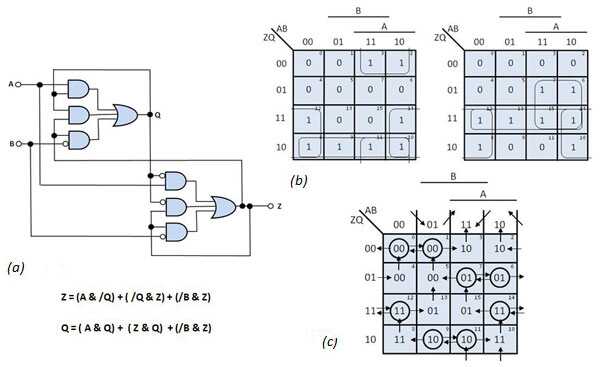
图3从该采样电路的逻辑图（a）中，您可以导出卡诺图（b）中的下一状态变量Z *和Q *。组合这些映射会产生电路的转换映射（c）。

假设系统以对应于平方1（ABZQ = 0100）的状态启动。如果A然后变为“1”，则总状态移动到方形3，其显示下一个状态“10”。方形3的状态不稳定，因为ZQ和Z * Q *不同。因此，电路状态移动到方形11，其中下一个状态是“10”。这是稳定状态（ABZQ = 1110），因为当前状态和下一状态是相同的。电路保持稳定状态（ABZQ = 1110）。

如果B然后变为“0”，则系统移动到方形10，显示下一个状态“11 “因为这种状态不稳定，系统状态在方形14处移动到稳定状态（ABZQ = 1011）。同样，您可以继续分析转换图的其余部分。参见图3 c用于所有可能的转换。

对于此电路，每次A置位，Z置位，当B置位时，Z复位。此行为描述了置位/复位翻转的特性-flop，其输出取决于输入边沿转换。

地图图表竞争条件

转换图提供了一种有价值的工具，用于分析竞争条件，当两个或多个下一个状态因输入值转换而同时发生变化时会发生竞争条件。以下示例有助于说明转换映射作为分析工具的用处：

案例1：在图4 a的电路，假设初始状态（ABZQ = 1101）。当转换图（图4 b）表示时，当前状态变量ZQ和下一状态变量Z * Q *是“01”。如果输入变量A变为“0”（AB = 01），则下一状态Z * Q *变为10. Z和Q同时变化，这将设置竞争条件。如果路径延迟Z和Q相等，电路经历以下转换：01-> 10-> 00。

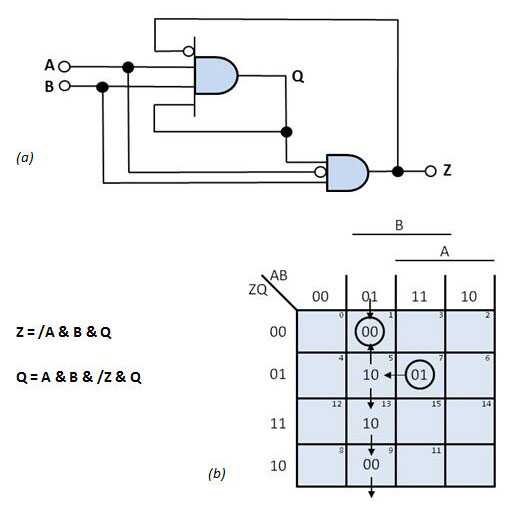
图4案例1：该电路（a）包含非关键竞争条件。如果电路在稳态ABZQ = 1101上电，则它可以以两种方式响应A中的负转变。如转换图（b）所示，两个响应都达到相同的结束状态。然而，稳定所需的时间随路径而变化。

因为Z和Q的路径延迟通常不同，但是从01到10的过渡不会直接发生，而是由两个中的一个发生。潜在序列：01-> 11-> 10-> 00或01-> 00。在这个例子中，电路在任何一种情况下达到相同的稳定状态“00”，这说明了一个非关键的竞赛。然而，在最终状态下稳定所需的时间仍然不确定，因为它取决于路径延迟。

案例2：在图5 a的电路中，假设起始状态为（ ABZQ = 1101）。如图中的映射所示，当A变为“0”时，以下序列是可能的：01-> 10-> 00,01-> 00或01-> 11。因此，两个不同最终的稳定状态可以用于输入转换。这是关键竞赛的一个例子。应该避免具有关键竞赛的电路设计，因为转换的结果是不可预测的。

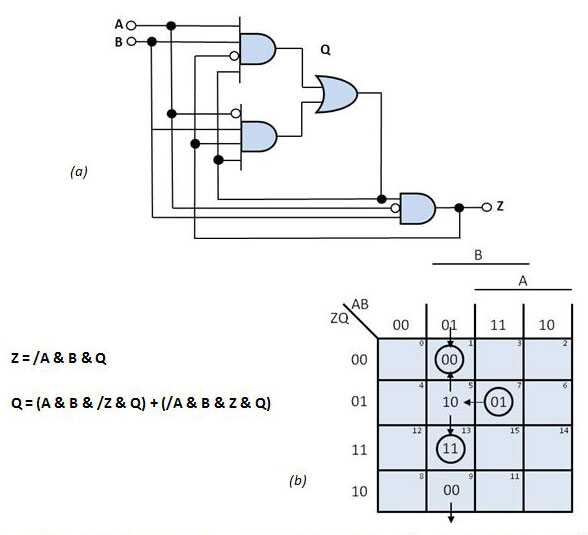
图5案例2：该电路（a）包含严重的竞争条件。如转换图（b）所示，电路可以在A变化后稳定在两种稳定状态之一。电路到达的状态取决于哪个逻辑块更快。

案例3：图6a 和过渡图中的逻辑图（图6 > b）对应于不稳定的电路。当AB从11变为01时，ZQ无限期地在不稳定状态“01”和“11”之间转换，即，输出Z振荡达AB = 01。在稳定电路的映射中避免这种行为。

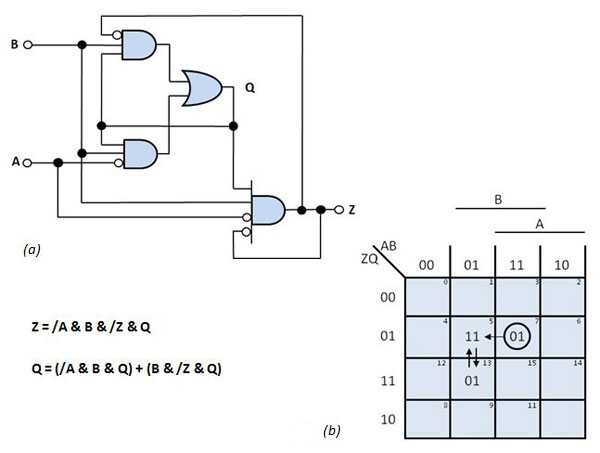
图6情况3：该电路（a）振荡时输入变量AB从AB = 11变为AB = 01。转换图（b）清楚地显示了危险。

通过分析这三种情况，很明显，为了正确操作和预测电路行为，有必要确保只有一个下一状态变量对于任何给定的输入转换都会发生变化。

使用地图计划设计

转换图不仅可用于分析异步电路，还可用于合成设计。例如，考虑设计一个电路，当B为高电平时，其输出Z跟随A的转换，当B为低电平时，电路保持稳定。对于任何给定的AB值组合，输出Z可以是“0”或“1”。该电路不能是简单的组合逻辑。它必须是顺序的，因为输出值取决于当前输入的值和先前的状态。这种电路的时序图出现在图7 a中。

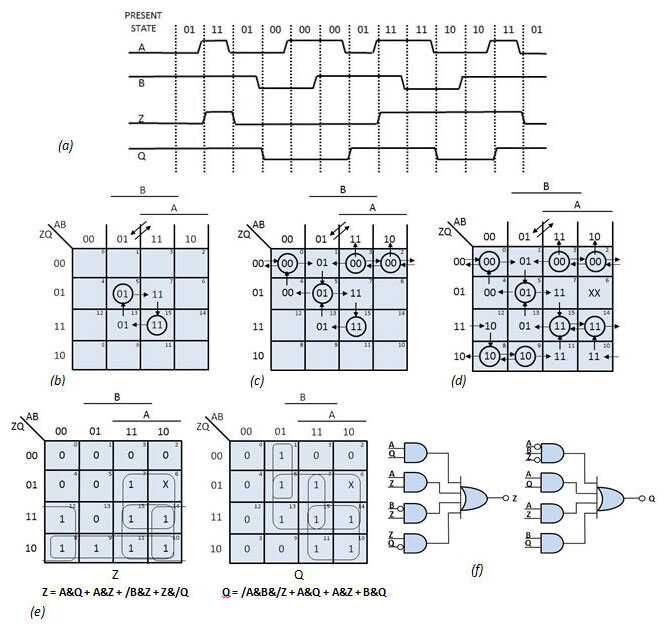
图7建议电路的时序图（a）显示，当B = 1时，Z跟随A，如果B = 0，则Z保持不变。为电路创建转换图（b）从假设的稳定状态开始，并用所需的下一状态值填充相邻的正方形，同时避免状态冲突（c）。最终的状态图（d）构成了卡诺图（e）的基础，从中可以得出最终的电路（f）。

设计这个电路的第一步是绘制转换图，假设您可以使用2状态变量状态机实现该电路。输出Z是当前状态变量之一; Q是第二个现状变量。由于电路具有两个输入变量和两个当前状态变量，因此转换映射包含16个方块（图7 b）。每个方块标识输入和当前状态变量的一个组合。

过渡图上方的箭头表示Z的所需过渡。如图所示，当B为“1”时，Z的变化遵循A的过渡。即，当Z从“01”变为“11”时，如果Z不是“1”，则Z从“0”变为“1”。如果Z，则Z从“1”变为“0”。当AB从“11”变为“01”时，该值不是“0”。没有其他输入转换会导致Z改变。

第二步是用适当的下一状态变量Z * Q *的值填充方块。请记住，Z *和Q *分别是在通过电路的传播延迟之后Z和Q所采用的值。 Z *和Q *实际上是虚拟变量，有助于理解电路的过渡行为; Z *和Q *没有物理现实。

按照以下几条规则填写过渡地图：

1。每次输入变量改变时，电路立即水平转换到标识新输入组合的列;即水平转换表示输入变化。

2。如果新的下一状态值与行值一致，则电路已达到稳定状态。

3。如果新状态不稳定，则电路在同一列内移动，直到下一个和当前状态变量相同。垂直转换表示输出变化。每个垂直状态转换需要一个传播延迟，因此，为了最大化电路性能，您的设计应该在达到稳定状态之前具有最小数量的垂直状态转换。

4。为了避免竞争条件，只有一个下一状态变量应该作为状态转换的结果而改变。

开始填充地图（图7 b），假设电路处于方形5（ABZQ = 0101）指示的状态，并且系统在该位置稳定。因为这表示稳定状态，所以下一状态等于当前状态，因此您可以在方块中写入“01”并在其周围画一个圆圈。

如果A现在变为“1”， Z也应为“1”，因为B = 1。电路水平转移一个方格到右方到方形7，在那里你写“11”，显示Z的变化，而Q保持不变。在这种状态下，Z * Q * = 11与ZQ = 01不匹配;因此，电路垂直移动（保持AB = 11）至方形15，其中ZQ = 11。在这个方块中，电路达到稳定状态，所以你可以写“11”并圈出它。

如果A再次从“1”变为“0”，“Z应该是”0 “新的下一个状态是”01“。现在，电路水平转换到13号方，你写”01“。因为Z * Q * = 01且ZQ = 11，所以该状态不稳定。因此，电路垂直移动到方形5，这是原始的稳定状态（ABZQ = 0101）。

到目前为止，电路符合要求，Z的值跟踪A的转换而B为真。剩下的要求是当B为假（B = 0）时Z不会改变。同样，从方形5开始（图7 c），当B从“1”变为“0”时，电路水平移动到方形4。 Z不应该改变，但你可能想要用新的总状态来识别这种转变。因此，切换Q的值，并在方形4处写入“00”。这是一个不稳定的状态，因此电路移动到方形0（ABZQ = 0000），在那里它将达到稳定状态，因为Z * Q * = ZQ = 00。写“00”，并在方块0处圈出。

避免状态冲突

如果A现在从“0”变为“1”，则“Z”应保持为“0” '因为B = 0（请记住，只有当B为高电平时，Z才会跟随A的变化。）电路水平移动到方形2（ABZQ = 1000），在那里达到稳定状态。用“00”填充这个方格，然后圈出来。如果B现在变为“1”，则电路在方形3（ABZQ = 1100）处移动到稳定状态，因此用“00”填充该方块并将其圈起来。如果A现在变为“0”，则Z保持为“0”，电路状态变为平方1.

此时，为Q分配值“0”或“1”。你将Q指定为“0”，Z * Q * = ZQ = 00，并且电路将在方形1处达到稳定状态。然而，这种状态分配存在一个问题：如果A随后从“0”变为“1”，然后Z应该从“0”移动到“1”，这将迫使方形3包含10作为其下一个状态。因为方形3的下一个状态已经是“00”，所以在方形1处赋值Q = 0导致状态冲突。

要避免状态冲突，必须在方形1（图7 c）中指定Q = 1。当方形1处的“01”时，状态不稳定并且电路状态垂直移动到方形5（状态ABZQ = 0101）。以类似的方式，通过其余状态来完成地图（图7 d）。

示例在方块5中的起始值是任意的。因此，转换映射中给定函数的状态赋值可能会有所不同，具体取决于初始选择并不总是有效。碰撞的发生可能会迫使您从不同的初始稳定状态重新启动转换映射状态分配。练习最终会产生最佳状态分配的直观知识，在达到稳定状态并消除所有潜在碰撞之前最小化转换次数。

一旦填写转换图，合成设计的第三步是从转换图生成卡诺图。每个next-state条目的第一个值对应于Z的值;第二个对应于Q的值。图7 e显示了该例子的卡诺图。

治疗不在乎

从这些地图中推断出相应的布尔方程。选择公式的乘积项时，请注意避免出现输出毛刺的电路。避免此类危害的经验法则是指定足够的产品术语以涵盖所有细节，并添加冗余的产品术语，以便相邻的产品术语重叠。

同样，您需要对待“不关心” （X）仔细。为它们分配有助于简化产品术语的值。然后，将这些值恢复到转换映射，并验证分配不会产生潜在的电路振荡，例如那些情况3 指示。

在图7 d中，square 6有一个不关心下一个状态。图7 e中的布尔方程假设方形6中Z * = 1且Q * = 1.如果在上电期间，电路进入对应的状态方波6（ABZQ = 1001），下一个状态为“11”，电路进入稳态ABZQ = 1011（方形14）。

设计综合的第四步（也是最后一步）是绘制Z和Q的逻辑图。如图7 f中的逻辑图所示，该实现包括2级门电路。这种类型的架构非常便于PAL实现和ASIC应用;它可以让您构建方便的专用模块，传播延迟最小。当前状态变量Z是电路的实际输出，Q是辅助变量。回想一下，Z *和Q *是虚构变量，代表异步电路模型中的下一状态值。当前状态变量Z和Q是物理存在且出现在电路逻辑图中的唯一变量。

通过使用更复杂和正式的程序，转换图分析可以处理具有三个或更多外部输入变量的电路。这种情况超出了本文的范围，但是，这提供了对异步电路的概念性理解。通常，同步电路可能更容易理解和设计。然而，当速度是高优先级时，异步逻辑就是答案。过渡地图分析可以指导您实现可靠的实施。