引言
实际光学系统的成像是不完善的,光线经光学系统各表面传输会形成多种像差,使成像产生模糊、变形等缺陷。像差就是光学系统成像不完善程度的描述。光学系统设计的一项重要工作就是要校正这些像差,使成像质量达到技术要求。光学系统的像差可以用几何像差来描述,包括:

•预备知识:
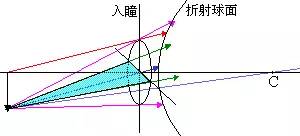
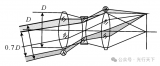
主光线:某视场点发出的通过入瞳中心的实际光线
第一近轴光线:轴上物点A发出的通过入瞳边缘点的“近轴”光线
第二近轴光线:轴外某视场点发出的通过入瞳中心的“近轴”光线
子午平面:包含物点和光轴的平面称子午平面
弧矢平面:包含主光线并与子午平面垂直的平面称弧矢平面
辅轴:轴外点和球心的连线称为该折射球面的辅轴
上光线:轴外点发出通过某孔径带上边缘的光线称某孔径带的上光线
下光线:轴外点发出通过某孔径带下边缘的光线称某孔径带的下光线
前光线:轴外点发出通过某孔径带前边缘的光线称某孔径带的前光线
后光线:轴外点发出通过某孔径带后边缘的光线称某孔径带的后光线
想一想:你能在图中找出对应光线或平面吗?
正弦条件和等晕条件
•正弦条件
首先我们考虑离光轴很近的轴外点,称近轴轴外点。
设轴上物点A→A’能以任意宽光束完善成像,则垂轴方向的近轴轴外点B→B’也能以宽光束完善成像需满足的条件称正弦条件。
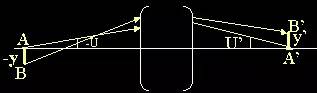
正弦条件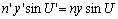 , , |
也可写成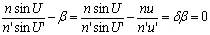 |
当物距为无穷远时,经公式变换,可将正弦条件写成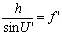 。
。
可以证明,齐明点满足正弦条件。
等晕成像和等晕条件
实际由于球差存在,只能要求近轴轴外点具有和轴上点A相同的成像缺陷。此时称等晕成像,需要满足的条件称等晕条件:

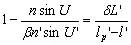 |
当物在无穷远时化为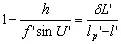 |
当球差为零时,等晕条件化为正弦条件。
当不满足等晕条件时,轴上点与近轴轴外点成像缺陷不等,用正弦差表示:
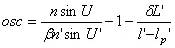 |
当物在无穷远时有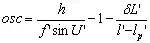 |
正弦差与孔阑位置有关,当球差不为零时,可以找到某孔阑位置使正弦差为零。
正弦差表征光学系统不满足等晕条件的程度。当正弦差不为零时,轴外点存在彗差。
轴外像差
由于折射球面存在球差和像面弯曲,使轴外点衍生出一系列像差。
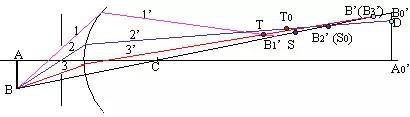

| 局部放大可画出各种轴外像差 |
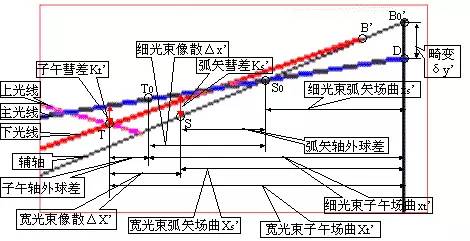
彗差
当系统不满足等晕条件时,轴外点存在彗差。
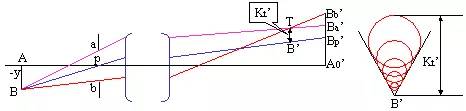
上下光线的交点偏离主光线:子午彗差
前后光线的交点偏离主光线:弧矢彗差
| 利用这些光线与高斯像面的交点高度来计算,其中前后光线关于子午面对称,它们与理想像面的交点高度必相等 |
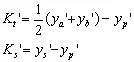 |
各环带上下、前后光线的会聚点相对于主光线不同,孔径大的偏离大,靠近主光线的偏离小,所以仅有彗差时,将形成彗星状的弥散斑。
不同孔径U有不同的彗差,不同视场W有不同的彗差,所以彗差和孔径、视场都有关。
像散和像面弯曲
对于宽光束,轴外主光线和共轴系统的光轴不重合,使出射光束失去对称,产生彗差、像散和像面弯曲;
对于细光束,彗差为零,但像散和像面弯曲仍然存在。
子午细光束像点在主光线上,弧矢细光束像点在主光线和辅轴的交点上,两者之轴向距离为像散。当视场由小变大时,子午细光束像点和弧矢细光束像点会偏离高斯像面。如果把各视场的子午细光束像点或弧矢细光束像点连起来,将会得到弯曲的像面,这就是像面弯曲。
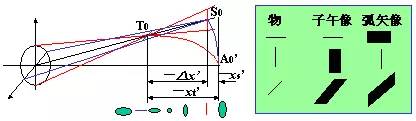
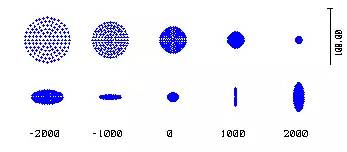
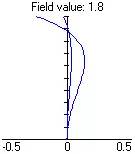
| 左图是对某具有很大像散和像面弯曲的光学系统的计算结果,表示了不同位置处的轴上点与轴外点单色光弥散斑,第一行是轴上点产生的弥散斑,第二行是轴外点产生的弥散斑,第三行数字表示位置,单位是微米。 |
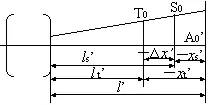
计算一条主光线,即可按下式计算并画出像散与像面弯曲曲线:
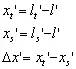 |
 |
|
| 本图形由软件GA画出 |
曲线中纵轴是视场,横轴是像面弯曲。将子午像面弯曲(用T表示)和弧矢像面弯曲(用S表示)画在一起,即可知道像散,不必另画像散曲线。
想一想:若像散为零,像面弯曲是否存在?
像散为零时,子午细光束像点和弧矢细光束像点重合,但不与高斯像面重合,所以像面弯曲仍然存在,这种像面弯曲叫匹兹凡面弯曲。
畸变
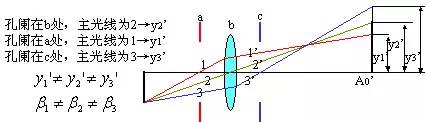
由图可见,当孔阑位置移动,主光线与高斯像面交点高度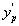 变化,引起像的变形。
变化,引起像的变形。
畸变仅是像的变形,不影响像的清晰度。有些光学系统只对清晰度要求高,对变形的要求可以降低。
实际像高比理想像高大,称正畸变,反之称负畸变。根据畸变的正负,等距的同心圆将会变成不同形状的不等距的同心圆,正方网格也会变成枕形或桶形。
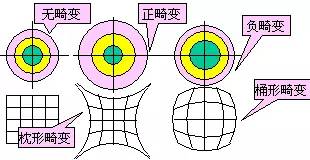
可用绝对畸变或相对畸变来度量畸变的大小。
绝对畸变又称线畸变: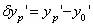 相对畸变是实际放大率与理想放大率的相对误差: 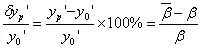 畸变曲线如右图。 |
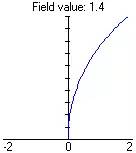 |
| 本图形由软件GA画出 |
畸变特征:
1.全对称系统(结构对称,物像对称),不产生畸变;
2. 孔阑与之重合的接触薄系统,不产生畸变(主光线通过系统中心,沿理想方向射出);
3. 对于单薄透镜,光阑前移——负畸变,光阑后移——正畸变。因此,畸变与光阑位置有关。
初级轴外像差
光学系统的初级轴外像差也可以用赛得和数来表示。一共有5个赛得和数。除了球差部分的第一赛得和数外,还有第二赛得和数至第五赛得和数,它们分别是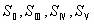 。
。
| 初级彗差 | |
| 初级像散与像面弯曲 |
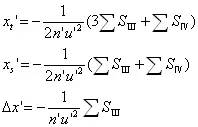 |
| 初级畸变 |
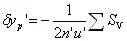 |
| 其中 |
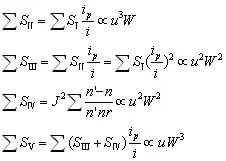
所以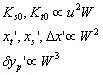 |
匹兹凡面弯曲
当像散为零即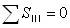 时,仍有
时,仍有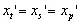 ,称为匹兹凡面弯曲。
,称为匹兹凡面弯曲。
这里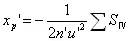 ,
,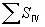 即第四赛得和数也叫匹兹凡和。
即第四赛得和数也叫匹兹凡和。
下面通过分析简单系统的匹兹凡和研究匹兹凡和的校正方法。
单个薄透镜的匹兹凡和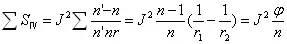
①单薄透镜的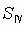 由 由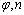 所决定 所决定 |
②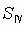 与 与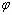 同号,与薄透镜形状无关。一般 同号,与薄透镜形状无关。一般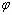 不为零。所以单薄透镜不能校正匹兹凡和。 不为零。所以单薄透镜不能校正匹兹凡和。 |
薄系统的匹兹凡和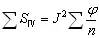
接触的薄系统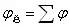 |
一般总光焦度>0,折射率相差不大,匹兹凡和不可能为零。 |
分离的薄系统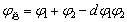 |
正正分离对校正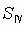 更不利,正负分离可校正 更不利,正负分离可校正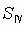 |
单厚透镜的匹兹凡和
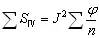 中 中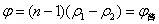 |
实际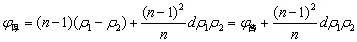 |
若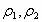 同号使 同号使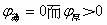 ,则可校正匹兹凡和。 ,则可校正匹兹凡和。 |
设该厚透镜要校正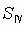 |
则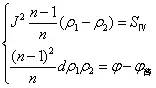 |
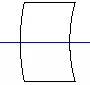 |
| 这样一块厚透镜可看成正透镜+平板+负透镜 | ||
|
结论:正负光焦度的分离是校正匹兹凡和的唯一方法 |
-
曲线
+关注
关注
1文章
82浏览量
20871 -
光学系统
+关注
关注
4文章
243浏览量
18352 -
清晰度
+关注
关注
0文章
7浏览量
6918
发布评论请先 登录
相关推荐
VirtualLab Fusion应用:畸变分析仪
全固态Nd:YAG激光器热效应及输出光束波前像差分析
头盔显示器设计参数简析
GLAD案例索引手册
[VirtualLab] 不同像差的焦点
人眼波像差测量中形心探测的新方法
单色像差有哪些分类
大视场超光谱成像差分吸收光谱仪光谱定标装置的原理及设计
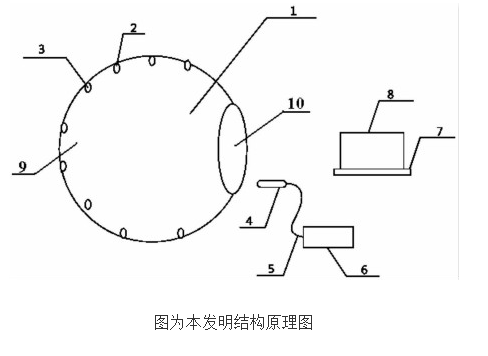
利用高级球差曲线分析光学系统
光学系统设计的不可忽略的参数介绍
机器视觉镜头的成像机理与特性解析
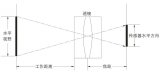
远心镜头的几个参数解析





 关于像差概论-轴外像差的分析和介绍
关于像差概论-轴外像差的分析和介绍










评论