信号发生器术语解释

●存储深度 ( 记录长度)

存储深度或记录长度与时钟频率一起使用，存储深度决定着可以存储的最大样点数量。每个波形样点占用一个存储器位置，每个位置等于当前时钟频率下采样间隔的时间。例如，如果时钟以100 MHz 运行，那么存储的样点间隔是10 ns。

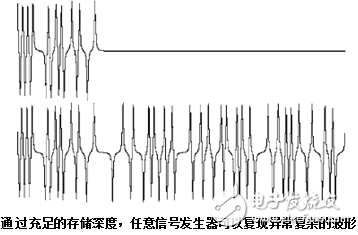
在许多频率上，存储深度在信号保真度中发挥着重要作用，因为它决定着可以存储多少个数据点来定义一个波形。特别是在复杂波形中，存储深度对精确复现信号细节至关重要。提高存储深度的好处可以概括如下：

※可以存储更多周期的希望波形，存储深度与信号发生器的排序功能相结合，允许仪器灵活地把不同波形联接起来，创建无穷多个循环、码型等等。

※可以存储更多的波形细节。复杂的波形在脉冲边沿和瞬态信号中可能有高频信息。很难内插这些快速瞬态信号。为真实地复现复杂的信号，可以使用提供的波形存储器容量，存储更多的瞬态信号和波形，而不是更多的信号周期。

●采样( 时钟) 速率

采样率通常用每秒兆样点或千兆样点表示，表明了仪器可以运行的最大时钟或采样率。采样率影响着主要输出信号的频率和保真度。内奎斯特采样定理规定采样频率或时钟速率必须至少是生成的信号中最高频谱成分的两倍，以保证精确地复现信号。例如，为生成1 MHz 的正弦波信号，必需以2 M 样点/ 秒(MS/s)的频率生成样点。尽管这一定理通常只是作为采集指导准则使用，但与示波器一样，其与信号发生器的相关性非常明确：存储的波形必须有足够的点数，以真实地重现希望的信号细节。

信号发生器可以获得这些样点，然后以规定极限范围内任何频率从存储器中读出这些样点。如果存储的样点集符合内奎斯特定理，并描述了一个正弦波，那么信号发生器将相应地滤波波形，输出一个正弦波。

计算信号发生器可以生成的波形频率需要对一些简单的公式求解，以存储器中存储了一个波形周期的仪器为例，假设100 MS/s 的时钟频率和存储深度或记录长度共4000 个样点，那么：

F输出= 时钟频率 ÷ 存储深度

F输出= 100,000,000 ÷ 4000

F输出= 25,000 Hz ( 或25 kHz)

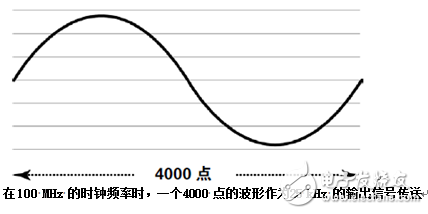
在规定的时钟频率上，样点距离约为10 ns。这是波形的时间分辨率( 水平)。为进一步推进这一流程，我们假设样点RAM 包含的不是一个波形周期，而是包含四个波形周期：

F输出= ( 时钟频率 ÷ 存储深度) x ( 存储器中的周期数量)

F输出= (100,000,000 ÷ 4000) x (4)

F输出=(25,000 Hz) x (4)

F输出= 100,000 Hz，新的频率是100 kHz。

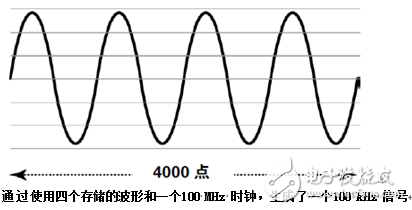
在本例中，时间分辨率仍为10 ns，但每个波形周期只用1000 个样点表示，产生的信号保真度要更低。

●带宽

仪器的带宽是一种模拟术语，它与采样率无关。信号发生器输出电路的模拟带宽必须足以处理其采样率将支持的最大频率。换句话说，必须有足够的带宽，能够传送从存储器中输出时钟的最高频率和转换时间而不会劣化信号特点。

●垂直( 幅度) 分辨率

垂直分辨率与仪器DAC 的二进制字长度( 单位为位) 有关，位越多，分辨率越高。

DAC的垂直分辨率决定着复现的波形的幅度精度和失真。分辨率不足的DAC 会导致量化误差，导致波形生成不理想。

10位分辨率的AWG 提供了1024 个样点电平，分布在仪器的整个电压范围内。例如，如果这个10 位信号源总电压范围为2 Vp-p，那么每个样点表示大约2 mV 的步进，这是仪器在没有额外衰减器的情况下可以提供的最小增量，其中假设它不受结构中其它因素的限制，如输出放大器增益和偏置。

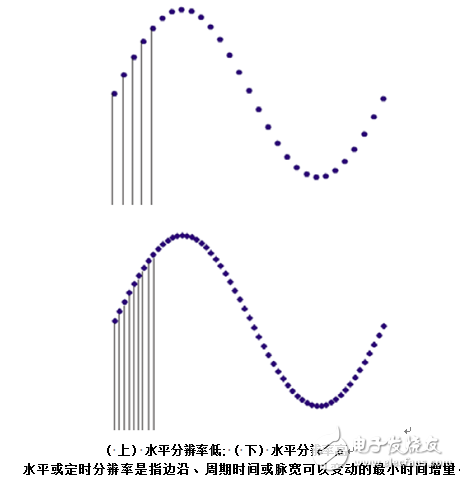
●水平( 定时) 分辨率

水平分辨率表示创建波形可以使用的最小时间增量。一般来说，这个指标使用下面的公式计算得出的。

T = 1/F

其中T 是定时分辨率，单位为秒；F 是采样频率。

根据这一定义，最大时钟速率是100 MHz 的信号发生器的定时分辨率是10 ns。换句话说，这一信号发生器输出波形的特点是由一串相距10 ns 的步进确定的。