本例电路使用LM324运放设计一款方波,三角波,正弦波的函数信号发生器。

电路分解:
整个电路的模块划分很明显,其结构如下:
一是由U1A和外围电阻,稳压管组成的迟滞比较器,产生方波信号;
二是由U1B组成的积分电路,产生三角波信号;
三是由U1C以及外围电阻电容组成的一阶低通有源滤波器,产生正弦波。
整个电路的工作过程如下:
电路中方波发生器和三角波发生器首尾相接,形成一个正反馈闭环系统。比较器U1A输出的方波经积分器U1B输出可得三角波,三角波又触发比较器自动翻转形成方波,这样即可构成三角波,方波发生器。同时,本例电路中,是采用运放组成的积分电路,因此可实现恒流充电,使三角波线性大大改善。
用比较通俗的话来讲就是当比较器输出使比较器的同相端电压高于0V时,比较器U1A输出翻转到高电平,即Uz+0.7V;当比较器的输出使比较器的同相端电压低于0V时,比较器U1A输出翻转到低电平,即-(Uz+0.7V)。
这样,当比较器输出高电平时,三角波的输出是向负向变化;当比较器输出为低电平时,三角波输出向正向变化。
这样不断的重复,就得到了三角波和方波。
其中方波的幅值受稳压管限制;而三角波的幅值大小为R8*Uz/R5。这个具体怎么得来的,可根据运放的虚短和虚断原理来计算。
正弦波输出原理如下:
三角波展开为傅立叶级数可知,它含有基波和3次、5次等奇次谐波,因此通过低通滤波器取出基波,滤除高次谐波,即可将三角波转换成正弦波。
但是低通滤波器的通带截止频率应大于三角波的基波频率且小于三角波的三次谐波频率。
图中U1C就是一个常见的反相输入一阶低通滤波器。实际上就是一个积分电路,其分析方法与一阶积分电路相似,但又与积分电路有不同的地方,下面是从网上所查到的关于这两者的一个分析,供大家参考:
某些文献上将积分器与RC低通滤波器混为一谈,但是,两者并不相同。
从传递函数上看:
积分器的传递函数是:Vout/Vin=ω0/s,而一阶RC低通滤波器的传递函数是:Vout/Vin=ω0/(s+ω0)。
可见,当信号频率远远高于ω0对应频率时,两者特性相当,也就是说,在高频衰减特性上,两者非常类似。
但是,对于低频的”低通“特性上,两者有本质的区别,信号频率低于ω0对应频率时,尤其是信号为直流时,低通滤波器输出等于输入,而积分器输出随时间变化,将上升至电路允许的电压上限(理想积分器将到无穷大)。
应该说,积分器与低通滤波器的高频特性基本相同,而低频特性有本质区别。
注意:
要想更好的理解本例电路,应该从数学计算入手,分析不同的输出函数受什么影响,然后根据这些分析来调节所得波形的一些参数,比如频率,幅值,相位等。
-
LM324
+关注
关注
15文章
166浏览量
65086 -
函数信号发生器
+关注
关注
6文章
68浏览量
14389
发布评论请先 登录
相关推荐
运放LM324失效
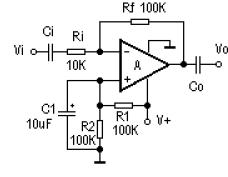
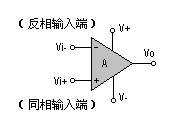
LM324 四运放集成电路的应用




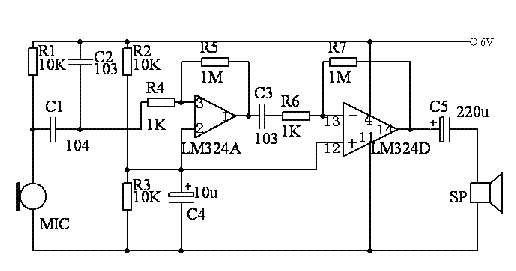
 使用LM324运放设计的函数信号发生器电路
使用LM324运放设计的函数信号发生器电路










评论