简单逻辑门与电路的介绍

步骤1：AND Gates

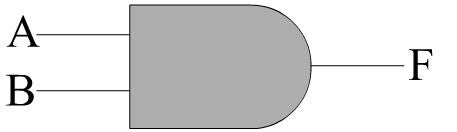
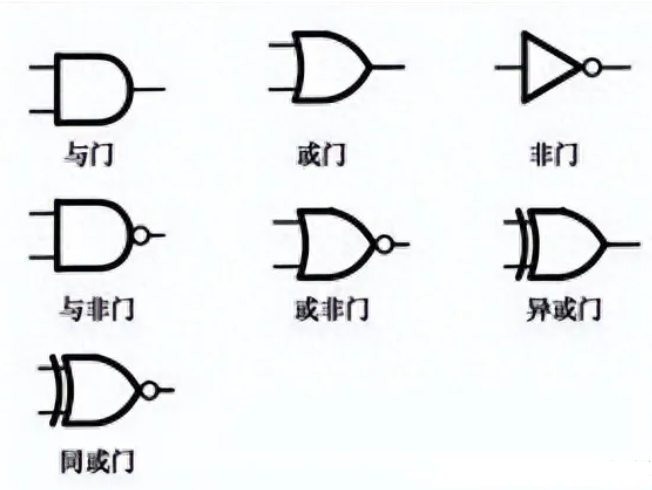
我们要看的第一种门是AND门。双输入AND门的电路符号是有趣的子弹形状的东西。标记为A和B的端子是输入，标记为F的端子是输出。

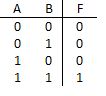
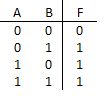
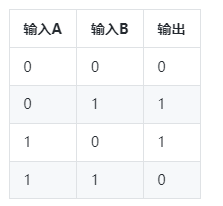
AND门通过以下规则确定其输出：如果两个输入均为1，则输出为1;如果两个输入中的一个或两个均为0，则输出为0（请注意，0和1分别是“低”和“高”电压）。 AND操作通常称为布尔乘法，因为结果就好像您“乘以”两个输入，并且也写为 F = AB ，类似于乘法。图下方的表称为真值表。这种表列出了所有可能的输入组合，并显示了它们相应的输出。这个特殊的真值表用于AND操作;注意，只有当两个输入都是1时，输出才为1，正如您所期望的那样。

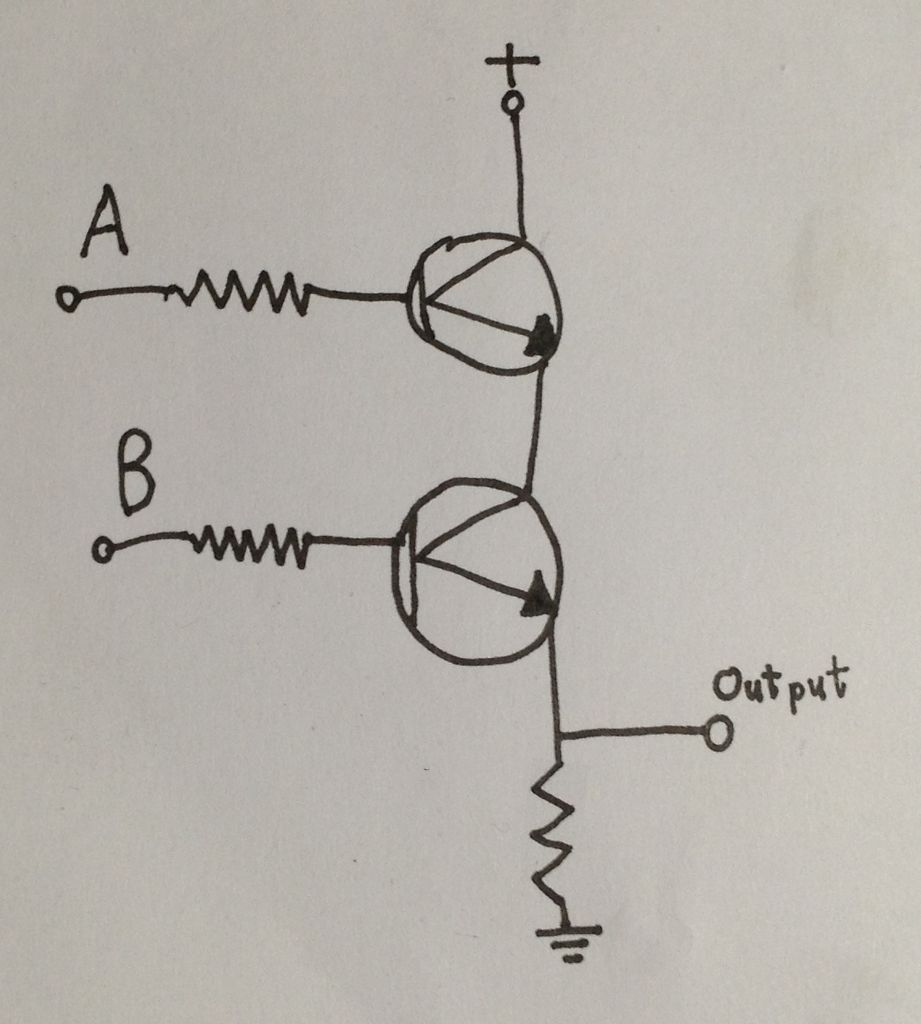
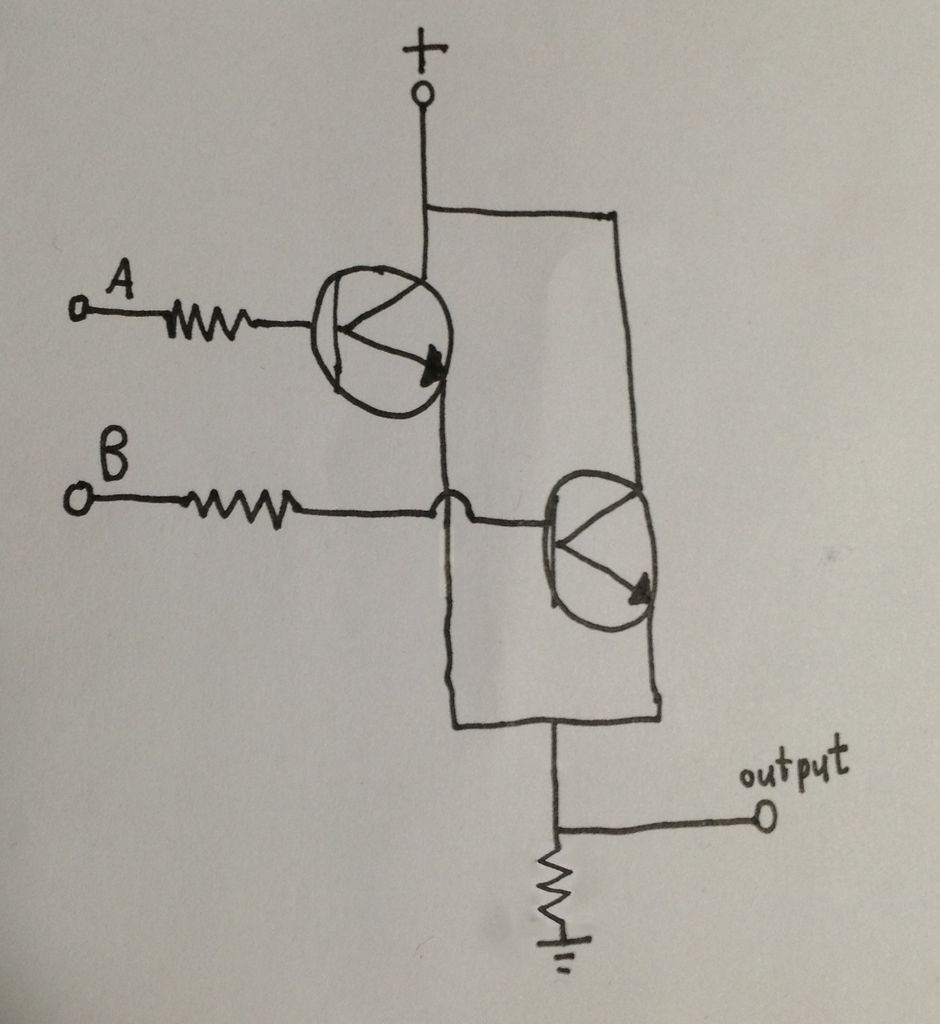
大多数逻辑门可以很容易地用晶体管制作。在上面的电路图中，您可以看到使用两个晶体管构建的简单AND门。是的，我意识到我的艺术技能从未离开过二年级。从本质上讲，这就像将两个开关串联起来。除非两个开关都闭合，否则电流不会流到输出。使用晶体管作为开关，可以完全用电子方式控制该电路。

现在看一下123D电路（单击此处）。您应该看到三个带有万用表的面包板。每个都是不同逻辑门的电路，每个万用表测量输出端的电压。第一个电路是我们要在这里查看的电路。按下“模拟”按钮，您会注意到一个很小的电压读数，约为几毫伏。这是正常的，并且小到可以忽略不计。朝向电路底部的两个开关就像输入一样。尝试先拨动其中一个开关，然后再拨动另一个。只需一个开关，您就会注意到电压稍微增加，但同样可以忽略不计。只有当两个开关都打开时，电压才会跳到任何可观的水平。这是AND逻辑门的基本工作。

步骤2：OR门

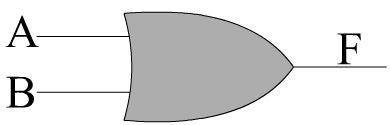
另一种类型的逻辑门是OR门。电路符号是箭头形状，输入和输出的标记方式与“与”门相同。

让我们看看OR门的真值图。如您所见，只要任何一个输入为1，输出将为1，并且只有当所有输入都为0时，结果才为0. OR运算也称为布尔加法，并相应地写入，如 F = A + B 。请注意，只有“高”和“低”电压，而没有“高”电压。因此1 + 1仍然等于1而不是2.请记住，所有这些操作都类似于数学运算，但不是严格相同的事情。

可以看到OR门相当于在输入和输出之间并联连接两个开关的电路。只要一个或两个开关都闭合，电流就会流动。

现在，让我们看一下123D电路中的第二个试验板。玩一下你会注意到晶体管按照提供的电路图并联连接。拨动任何一个开关后，您应该会看到电压立即跃升至7伏。仅当两个开关都关闭时，输出才会像您期望的那样下降。

步骤3：非门与组合

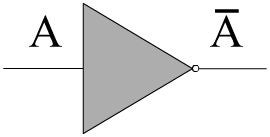
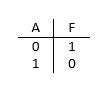
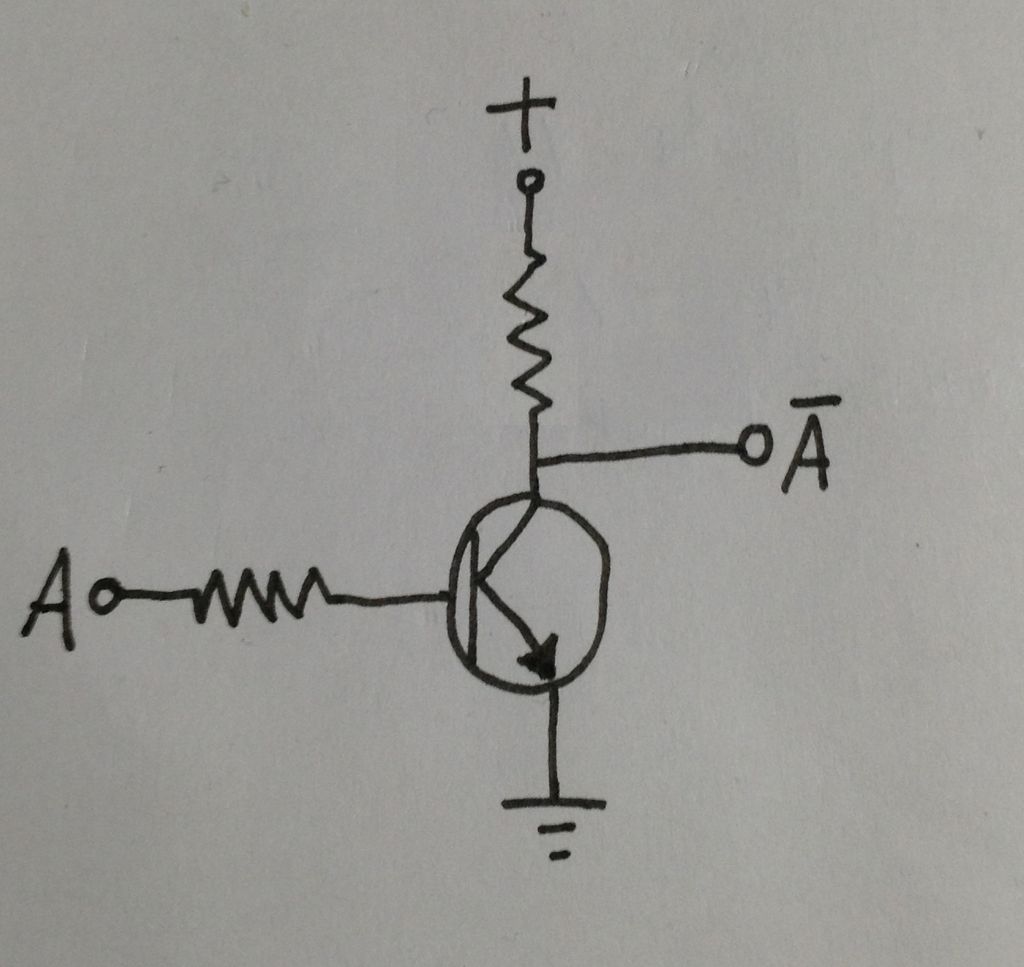
“非”门为比较简单。它只有一个输入，它所做的就是获取输入的值并将其取反。它有一个非常简单的真值表来说明这一点。输出为 F = A̅（读取A-bar）。条形图表示反转，因此A̅只是 A 反转。

现在让我们回到123D电路，将注意力转移到最后的实验板上。打开时，输出将为低电平，关闭输出时输出将为高电平。现在让我们尝试一些不同的东西。取下AND门输出电阻和面包板接地之间的连接，然后将电阻连接到开关正上方的NOT门输入端（确保NOT门的开关关闭）。注意这是什么？现在，“与”门的输出是“非”门的输入，而“与”门将使“与”门的输出反相。您可以使用OR和NOT门，甚至AND和OR门执行类似的操作。基于晶体管的逻辑门可以像这样几乎无限地串在一起。随意玩一下，使用123D电路的最好之处在于，您可以进行实验而无需花费成本，也不会损坏实际零件。

在下一节中，我们将采用进一步组合的想法，讨论基于所需真值表设计特定逻辑电路，并结束使用目前所讨论的所有内容的详细示例。

第4步：逻辑电路综合

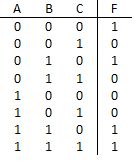
逻辑门可以用许多不同的方式串联起来。每个组合为您提供不同的布尔“函数”。在这里，我们概述了两种设计逻辑电路的简单方法，该逻辑电路产生了我们想要得到的确切真值表，在本例中是上面显示的表。

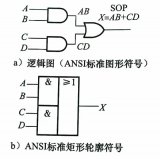
产品总和（SOP）

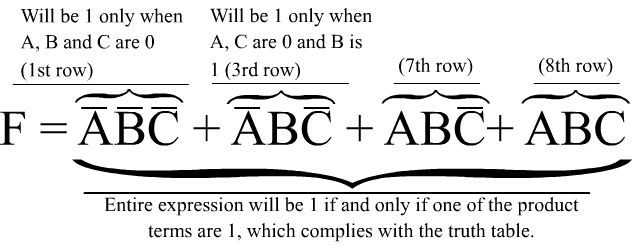
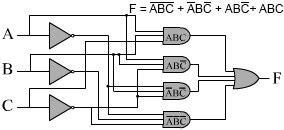
在这种方法中，我们专注于真值表的行，这些行需要产生1的输出。现在，让我们看第一行。请注意，如果我们将0个输入（在此行中的所有输入）取反并将它们相乘（这将通过3个输入的AND门完成），则当且仅当条件满足时，我们将得到一个为1的函数。满足第一行：仅当 A = B = C = 0时，A̅B̅C̅为1。该产品将成为我们“产品总和”中的条款之一。让我们看下一行 F = 1，这是第三行。当它们相乘时，我们需要将哪些输入反转以确保值为1？ A 和 C 为零，因此必须取反。结果为A̅BC̅，这将是我们总和的第二项。以同样的方式，第七行和第八行给我们ABC̅和 ABC 作为第三和第四项。请注意，当我们将所有条款加在一起并设置 F = A̅B̅C̅ + A̅BC̅ + ABC̅ + ABC 即可。这些术语中的每一项只有一组特定的输入才为1。通过将它们加在一起，当其中任何一项为1时， F 将为1；如果它们都不为1，则为0（上图）。因此， F 符合我们的真值表。现在我们只需要构建函数 F 描述的逻辑电路。您可以在上面找到电路图。

求和产品（POS）

第二种设计逻辑电路的方法与第一种方法非常相似。已经讨论过您可能已经猜到了，当使用乘积法时，我们不将乘积相加，而是乘以和。

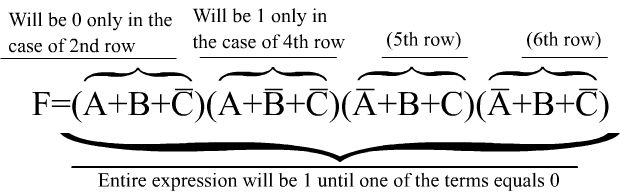
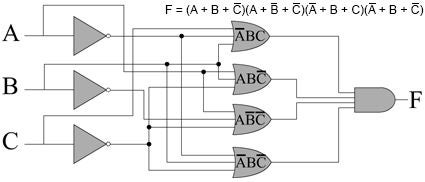
我们而不是看结果为1的真值表的行，而是看结果为0的行。让我们看第二行。这些输入将产生多少总和？如果将C取反，然后将其加到A和B，我们将得到0 + 0 + 0 = 0。因此，此行的术语是 A + B + C̅，仅在第二行的情况下等于0。转到第四行，很明显，我们需要反转 B 和 C ，为我们提供 A + B̅ + C̅。继续进行第六行，我们得到了四个术语： A + B + C̅， A + B̅ + C̅，A̅ + B + C ，A̅ + B + C̅。注意如果将它们相乘会发生什么： F =（A + B + C̅）（A + B̅ + C̅）（A̅ + B + C）（A̅ + B + C̅）。只要我们的总和中的任何一个等于0， F 将等于0.只有当它们全部等于1时， F 等于1.这完全符合真值表。上图中给出了该电路的一种可能的实现方式。

简化

很明显，真值表的两个电路非常复杂，比他们需要的更多。逻辑表达式可以简化很多，大致相同，如果它们纯粹是数学表达式，它们可以被简化。

与基本代数一样，一些属性适用：

AB = BA

A（BC） = （AB）C = ABC

A + B + C = A + （B + C） = （A + B） + C

A（B + C） = AB + AC

由于我们正在处理布尔代数，因此我们还有一些其他属性，我相信它们是相当不错的直观：

AA = A

AA̅ = 0

A + A = A

A + A̅ = 1

一旦完成这些简化就是小菜一碟。这是一个简单的示例。

说 F = A̅B̅D + A̅BD + BCD + ABC 即可。如果直接实施，该电路将相当复杂，需要七个门来完成。让我们简化一下。

请注意，A̅D可以在第一学期和第二学期中计算出来，给我们 F = A̅D（B̅ + B） + BCD + ABC

自B̅ + B 总是等于1，它掉出来，剩下 F = A̅D + BCD + ABC

下一步更直观一点。 BCD 仅在B，C和D均为1时等于1。但是在这种情况下，A̅D等于1或 ABC 等于1（检查一下）。此外，如果任何一项为1，则结果为1，因此 BCD 项完全多余，可以删除。这样我们得到的最终结果为 F = A̅D + ABC 。这是设计电路要容易得多的表达，并且只需四个组件即可完成，这是一个巨大的改进！如果您感到好奇，可以为初始表达式和最终表达式编写真值表，并查看它们是否相同。

接下来，让我们把目前为止学到的所有内容都用在一个真实世界的大例子中！

第5步：最后的例子

作为此Instructable的宏大结尾，我们将尝试将前面步骤中的所有内容组合成一个巨大的示例。如果您掌握了目前为止涵盖的所有内容，那么它应该相对容易一些，并且如果仍然有一个或两个概念对您而言还不十分清楚，那么您应该可以澄清这个示例。

您的任务是设计控制牙膏旋盖机开机机制的电路。电路应根据以下规则确定机器是否通电：

除非安全已脱离，否则机器不会通电。

除非已将牙膏盖装入机器，否则机器无法开机。

如果发生错误或故障，机器无法启动。

有一个手动超控功能，可在不考虑操作盖和警告的情况下打开机器。

我们有四个输入： S 在安全性打开时为1，在安全性关闭时为0。加载所有大写字母后，输入 C 变为1。如果出现任何错误或故障，输入 E 变为1.输入 O 由手动超控开关控制，如果打开则为1。仅当满足给定条件时，输出 P 才打开（1）。我们需要做的第一件事是制作一个真值表，让我们看看如何做。

真相表

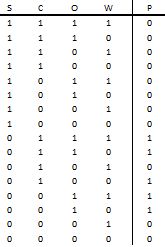
这部分可能是在铅笔和纸上更容易，所以去抓一些自己。现在绘制您在所有真实图中看到的表格，并标记输入S，C，O和W以及输出P.下一步是记下每个可能的输入组合;因为我们有4个输入，所以我们应该得到总共2 ^ 4 = 16个组合。一旦完成，我们必须弄清楚每组的输出。如果我们暂时考虑一下，我们可以大幅减少所需的工作量。从规则中注意，如果安全装置仍处于打开状态，则机器将永远不会开机。这表示 S = 1， P = 0的任何地方。就像完成了一半的输出一样。接下来让我们看一下手动覆盖。对于其余的八个组合，只要启用了覆盖，无论其他两个输入如何，输出都将为1。那应该再减少四个，再减半！现在让我们系统地看看其余四个。请注意，真相表中的顺序可能会有所不同，具体取决于输入的顺序。在我的桌子上，下一个空白是 S C O E 等于0 1 0 1.由于 E = 1，输出将为0（规则3）。接下来，当 SCOE 等于0 1 0 0时，我们发现 P = 1是因为安全性已关闭，瓶盖已装入，并且未发生符合所有规则的错误。继续 S C O E 等于0 0 0 1.我们从输入中看到尚未加载上限（规则2）并且已检测到某些错误或故障（规则3）。由于尚未启用手动优先功能，因此机器不应启动并且 P = 0。最后，最后一个空白是所有输入均为0的地方。显然没有再次加载大写字母，所以 P = 0。

现在，您的真值表应该已经完成，您可以对照上面提供的内容进行检查。同样，您的订单可能会有所不同，但相同的输入应该产生相同的输出。下一步是提出一个满足真值表的函数。

电路设计

在这里，我们可以选择使用POS还是SOP。查看输出列，我们看到很多很多0，但只有几个1。使用SOP方法似乎更简单，因为这样我们的函数中要处理的术语就会减少。

我们有五行输出为1。它们是：（按 SCOW的顺序） 0111、0110、0100、0011和0010。比较容易发现我们的产品总和是 P = S̅COW + S̅COW̅ + S̅CO̅W̅ + S̅ C̅OW + S̅C̅OW̅ 》

这是尝试构建的相当复杂的电路，所以让我们看看如何简化。显然我们可以拿出S̅，如果我们在可能的情况下拿出 CO 和C̅O，我们会得到 P = S̅ ［ CO （ W + W̅）+ C̅O（ W + W̅）+ CO̅W̅］

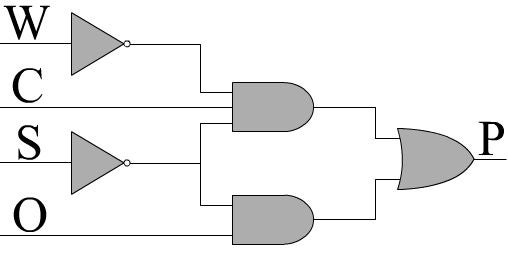
记住添加到其反向的输入始终等于1（检查上一页的标识），我们可以从头开始（ W + W̅），然后留下 P = S̅（ CO + C̅O + CO̅W̅）。最后，如果我们拔出 O 并划出最终的 C + C̅术语，我们的结果将为 P = S̅O + S̅ CO̅W̅。这可能是我们在数学上所能达到的最大范围，但是仍然可以进行进一步的简化。两个术语中都有 O ，一个是倒置的，一个是非。这通常表明我们可以尝试进一步简化。让我们看看是否可以。显然 O 是1或0。如果它是1，并且S̅也是1，则左项将是1，使 P 1。如果 O 为0且S̅CW̅ = 1，则再次 P = 1.但请注意，如果S̅， C ，W̅均等于1，然后 P = 1，无论 O 。在这种情况下，如果 O = 1则第一项将等于1（S̅ O = 1），如果它等于0则第二项term等于1（S̅CO̅W̅ = 1）。因此，我们发现如果S̅， C 和W̅为1则 O 无关紧要，可以从那个词。实际上，这意味着如果安全开关已关闭，安全帽已装上且没有任何警告有效，则无论手动超控功能是否打开，机器都可以开机（查看真值表，您会发现这是真正）。现在，我们的最终结果是 P = S̅O + S̅CW̅，更实际的不是它。上面显示了此功能的一种可能的实现方式。请注意，与我们开始使用的原始SOP相比，它使用的组件很少。

那里有！在几分钟的时间内，我们解决了一个问题，找到了解决方案，对其进行了优化并实现了结果。这本Instructable几乎无法触及数字电子技术的奇迹，但希望您对它有了基本的了解和赞赏。然后，这就是Instructable的结论，我希望它能启发您设计和制作自己的东西。
责任编辑：wv