怎样用Python制作数值积分程序

步骤1：了解算法第1部分：定积分及其使用

我假设您对基本演算的背景了解一点积分。积分很重要，因为它们使您可以将值数组乘以 infinitesimal 长度求和；这在金融，数论，物理，化学以及许多其他领域中很有用。但是，该程序仅允许您计算有限间隔内曲线下方的面积，换句话说，它不会评估反导数-要使用更强大的算法，那。如果您需要在针对其他对象指定的较大程序中求值定积分，或者要检查答案是否需要手工完成，则此算法很有用。

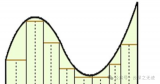
基本定积分表示函数定义的曲线下的面积，例如F（X）。对于确定的积分，我们求两点之间的面积（分别标记为a和b）。在图片中，绿松石区域是我所指的区域，并且确定该区域的公式也显示在该区域中。图片中显示的功能是任意的。

步骤2：了解算法第2部分：数值逼近

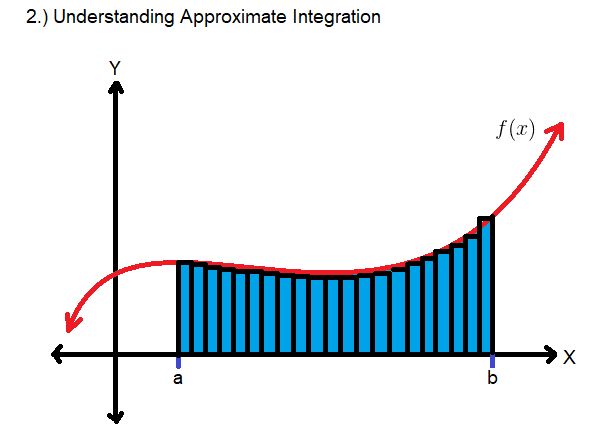
计算机需要大量的指令来计算该面积在可用于任何功能的任意函数下，因此您可能熟悉的分析方法没有用，因为它们太特殊了。一种计算机可以实际处理的近似计算积分的方法是，用感兴趣的区域填充用户定义的宽度和高度可变的矩形，然后对所有矩形区域求和，从而完成计算。矩形的刚性将使某些总面积保持不变，因此为什么将其视为近似值；但是，您可以在边界（a和b）之间填充的矩形越多，由于未触摸的区域变得稀疏，所以近似值越准确。由于计算机将执行此任务，因此可以将所需区域中的矩形数量设置为非常大的数量，从而使逼近非常精确。在支持图片中，假设指定区域中的每个矩形都具有相等的宽度。我尽了最大努力使它们在Microsoft Paint中具有相等的宽度，但没有做得最好。

步骤3：了解算法第3部分：中点规则

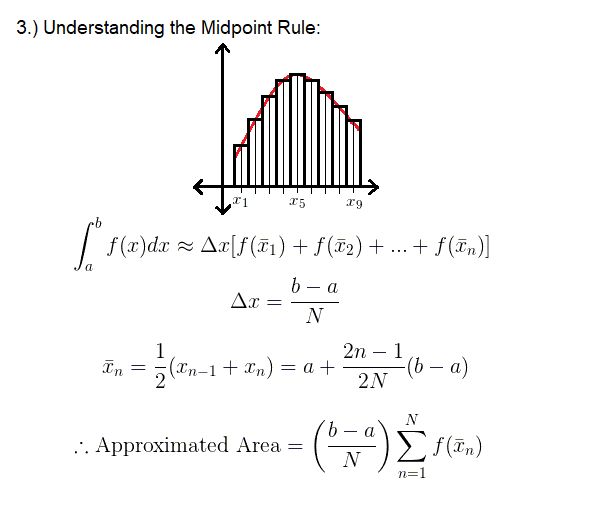
此规则指定如何在矩形中制作和使用矩形近似值。 “ N个”矩形中的每个矩形必须具有相等的宽度Δx，但每个第n个矩形不能完全相同：变化因子是高度，它随在某个点求值的函数而变化。中点规则之所以得名，是因为您将每个矩形的高度评估为f（x_n），其中“ x_n”是每个矩形的相应中心点，分别位于矩形的左侧或右侧。使用中点就像实现平均值，比起使用右或左时，将使近似值更准确。此步骤的辅助图片总结了如何在数学上定义中点规则。

第4步：创建程序第1部分：下载Python编译器/编辑器

现在，您了解了需要实现的算法，即让计算机为您执行计算的问题。告诉计算机该怎么做的第一步是获取执行此操作的工具。该算法可以用任何语言编码。为简单起见，该程序将使用Python语言进行编码。要命令您的计算机执行Python操作，您将需要一个编辑器，该编辑器以该语言编写指令，然后将其编译为计算机可以理解的机器语言，从而可以执行您要执行的任务。在当今时代，通常将编辑器和编译器集成在一起，但是并不总是如此。您可以使用任何您喜欢的编辑器/编译器，但我将向您展示如何获取我个人最喜欢的Python：Canopy。如果您已经具有编辑器/编译器，则可以跳过这些步骤。

转到https://www.enthought.com/product/canopy/

单击下载机盖

单击与您的操作系统相对应的下载按钮

下载将自动开始。

启动后，请按照滴注说明进行操作执行文件

运行程序

从程序主菜单中单击“编辑器”

在屏幕中央单击“创建新文件”

从这一点开始，您应该看到一个空白的白色窗口，其光标类似于基本的文字处理文档。现在您可以开始编码用于求解定积分的数值积分算法了。后续步骤将提供您要复制的代码片段，并说明该代码片段对整个程序的作用。

步骤5：创建程序第2部分：导入函数和定义变量

将代码复制到图片中。

对于您可能会发现自己进行编码的任何程序，都会有变量。变量是给将要操作并且可以更改的值的名称。在大多数编程语言（如果不是全部）中，您必须先初始化变量，然后程序才能对其进行更改。在此程序中，我将变量命名为“ N”，“ a”和“ b”。这些值分别表示迭代数（矩形的AKA数），下边界和上边界。您可以随意命名这些名称，但要匹配“理解算法第3部分：中点规则”中给出的公式，最好使其保持不变。请注意，它们不仅设置为特定值。这是因为将它们作为输入，以便在运行程序时，程序的用户可以定义值。输入命令后，引号中的文字会在您运行程序时显示，告诉您要键入哪种类型的值。您还将注意到，在输入名称之前使用了“ int”和“ float”。这些术语告诉计算机此值将是什么类型的变量。 “ int”是整数，“ float”是浮点值（即十进制）。应该清楚为什么要这样指定它们。

在“＃”之后出现的任何文本都是注释，它使程序员可以以人性化的方式遵循代码；我已经在您的代码中做了一些注释，您将复制这些注释，但是可以随意添加任何对您有帮助的注释。该程序将不会读取任何带有“＃”作为命令的内容。

读取“ from math import *”的代码部分告诉程序导入一系列可以使用的数学函数无需自己编写程序。 “ *”仅表示“全部”。将这部分代码读为：从数学库中导入所有函数。这使您可以使用数学函数，例如正弦，余弦，对数，exp等。这些函数可以数学方式集成在代码中。

第6步：创建程序第3部分：创建集成函数

将代码复制到前一个下方的图片中码。

警告：本部分内容繁琐，我想清除一些可能引起混淆的内容。在谈论编程时，“功能”一词会弹出很多。当您谈论数学时，这个词也会弹出很多。因此，从这一点开始，当我在编程意义上谈论一个函数时，我将写“ Python函数”，而当我谈论数学函数时，我将说“数学函数”。在某些时候，我们将使用Python函数作为所讨论数学函数的表示形式。

下一段代码是程序的核心。在这里，定义了一个Python函数，该函数使用中点规则执行数值积分算法。 “ def Integrate（N，a，b）”的读法是：定义一个名为“ Integrate”的函数，该函数接受变量“ N”，“ a”和“ b”，并返回曲线下方的面积（数学函数）这也在“集成” Python函数中定义。您可以在进行编码时以任何方式调用此Python函数，但是将其称为集成是有意义的，因为它确实集成了数学函数。

在这一点上，值得一提的是Python隔离代码块。代码块是执行特定任务的整个部分。不同的编程语言将具有指定的方式来区分这些“块”。对于Python，一个块通过缩进来区分：每个执行任务的部分都有自己的缩进，并且其他缩进块中也可以有缩进块。这代表了任务中的任务，并从根本上告诉了代码执行的顺序。对于已定义的Python函数“集成”，该函数中的所有内容都缩进一个块，从而区分将在该函数中执行的任务。这个Python函数中的缩进部分也执行自己的任务。内容如下：列出命令（任务），在命令后面加冒号，并在其下方缩进该命令的内容。

在定义“集成” Python函数之后，您将立即定义另一个称为f（x）的Python函数。这表示将要积分的数学函数。对于要集成的每个不同的数学函数，您都必须转到此程序行以对其进行更改（与运行程序时定义的变量不同）。每个Python函数都会有一个返回值，这就是当您将其赋值时该函数返回的结果。在这种情况下，抛出的值是“ x”，而这个“ x”项将采用您抛出的值的值，它是一个临时值。

接下来，是一个for循环充当本教程“理解算法”部分的公式中定义的求和。此求和需要更多几个变量，其中一个将作为整个“ Integrate” Python函数的返回值。在for循环之前，我已将这些变量指定为“ value”和“ value2”。 for循环的任务是遍历指定变量的值范围，该变量可以在for-loop命令中方便地定义；在这种情况下，该变量为“ n”。发生迭代的范围是1到N + 1。您应该注意到，上述公式中定义的总和范围仅从1到N。我们用这种方式进行定义，因为Python语言会从0开始对每个迭代值进行计数，因此我们必须从本质上转移这些值的范围以适应我们的期望范围。然后，for循环允许将所有矩形的高度加在一起，并将该值存储到我称为“值”的变量中。这在显示为：value + = f（a +（（n-（1/2））*（（b-a）/N）））的代码段中可以看到。

从那里开始，下一段代码使用名为“ value2”的变量，然后将其分配为每个矩形的所有高度的总和乘以每个矩形的标准化宽度。是我们要在程序中显示的最终答案，因此是“集成” Python函数的返回值。

第7步：创建程序第4部分：显示答案

将代码复制到先前代码下方的图片中。

现在，可以通过“集成” Python函数获得答案了，我们希望能够显示它。这只是将用户输入的值（“ N”，“ a”和“ b”）放入“集成” Python函数并将其打印在屏幕上的问题。该命令显示在第21行，它实际上是完成该步骤所需的全部操作。第19和20行上的代码仅用于“修饰”整个程序的输出。 “ print（” 。..。..。..。..。..。..。..。..。..。..。..。..。“）”将程序的输入部分与输出部分分开，然后“ print （“这是您的答案：”），仅表示将在该行文本之后打印答案。

步骤8：运行程序第1部分：按原样运行程序

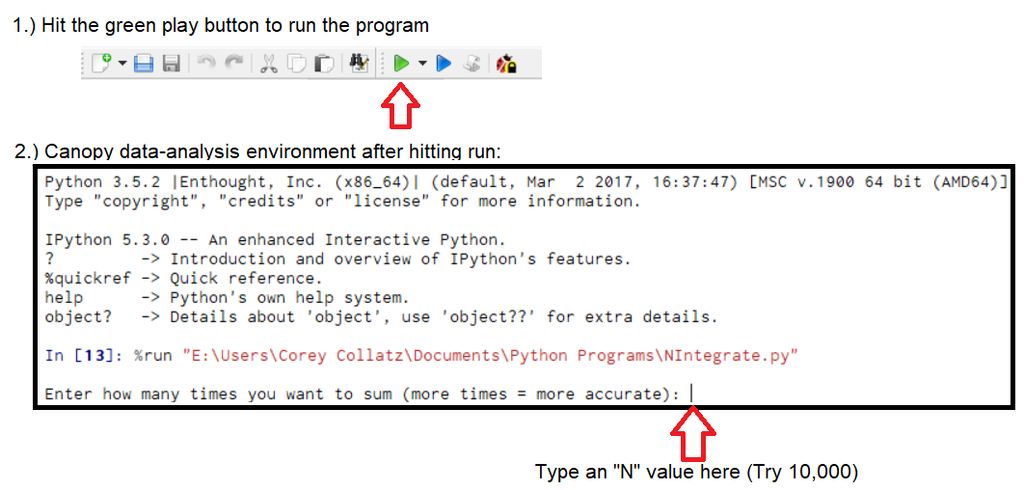
如果您不使用Canopy，则您甚至可能根本不需要执行此步骤，并且运行该程序可能需要不同的过程。在Canopy中，您必须先保存它，然后才能运行该程序。 Python程序的文件类型是.py文件-它会自动保存为。选择要保存文件的位置，然后就可以运行该程序了。

运行程序：

在显示文件名的工具栏上方，点击看起来像“播放按钮”的绿色按钮（请参阅图片） ）。

然后该程序将在称为Canopy数据分析环境的编辑器的底部屏幕中运行。假设您复制了我编写的提示，则应该在Canopy数据分析环境的底部看到提示：“输入要累加的次数（更多=更准确）：。”。 （请参阅图片）

输入一个值，表示要执行多少次迭代，即10000（要推入您所在区域的矩形数），然后按Enter键。

将出现更多的提示，这些提示应该是您在步骤5中编码到程序中的熟悉的输入提示。

应该对积分求值，并且应该显示结果。

如果您如上图所示对程序进行编码，则您刚刚积分了f（x） = x ^ 2在一定范围内。 x ^ 2的积分很容易手动计算，因此您应该检查并确保程序对手动确定的正确分析值给出了非常接近的答案。当我使用N = 10000，a = 0和b = 10的值运行程序时，得到的答案是333.33333249999964。正确的分析答案是333.333。这是非常准确和快速的。实际上，您已经在x轴上挤压了10，000个介于0和10之间的矩形，并使用它们来近似计算曲线x ^ 2下的面积！

步骤9：运行程序第2部分：集成其他数学函数

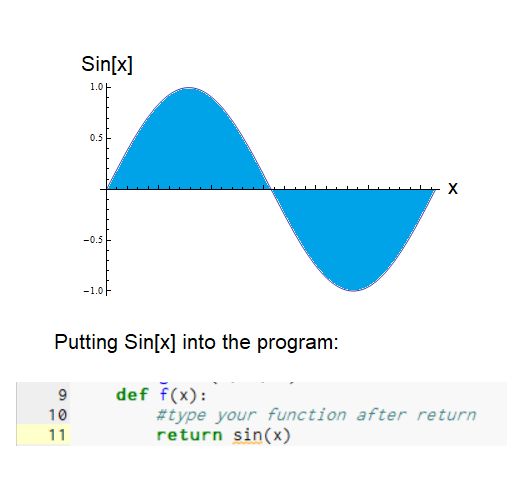
在上一步中，如果您一直在关注忠实地，您对f（x）= x ^ 2进行了积分。这不是该程序可以集成的唯一数学函数。在第5步中，您已经将Python函数的数学库数组导入程序中。这使您可以使用可以集成的更复杂的数学函数。让我们试一试。当然，您可以使用任何想要的函数，但是我将通过集成一个特定的数学函数来进一步证明该代码的准确性，该数学函数在一定范围内集成时会产生一个众所周知的值。该函数为f（x）= Sin ［x］。此数学函数显示在第一张随附的图片中，从0到2π进行绘制，并且感兴趣的区域以绿松石阴影显示。在此间隔中，正面积与负面积相等，因此，如果将总面积相加，则应该为零。让我们看看这是否真的发生：

将数学函数f（x）= Sin ［x］放入程序中：

再次运行程序之前，在注释下“返回后#type您的函数，”键入：sin（x）当前位于x ** 2的位置。 （参考图片）。

再次点击绿色的播放按钮运行程序。

输入10000作为N值（您希望求和多少次）。

输入“ 0”作为下边界。

将6.2832输入上边界（大约2π）。

看看您能得到什么价值。

当我这样做时，最终得到的价值是1.079e-10：这等于.0000000001079，这实际上是接近于零，因此它看起来确实是准确的，并且表明该算法足以处理负区域。

步骤10：运行程序第3部分：扩展程序

至此，您已经完成：您已经在其中编写了一个有效的确定积分算法可以平稳运行并给出非常准确答案的Python。但是，可以改进此程序。我不是程序员，并且对Python的经验很少。实际上，我不得不重新学习如何使用Python来完成本教程，但这应该使您相信Python是一种易于学习的语言。我的观点是，您可以通过提高程序效率来扩展该程序，也许可以实现一些GUI，并使其更加用户友好。

我对扩展程序的想法：

实现一个图形用户界面，使您无需使用Canopy交互式数据分析环境即可运行程序

对其进行设置，以使无需集成要集成的数学函数程序，但可以在程序运行后输入（我最初是想这样做，但无法弄清楚）。

定义一个“集成” Python函数，以便将f（x）函数视为在其中定义了f（x）函数的地方。

这些是只是一些需要改进的例子，但我保证还有很多其他可以改进的地方。因此，我将这一步骤作为该程序存在缺陷的一个示例，并作为任何想进一步改进该程序的人的练习。
责任编辑：wv