不同于针对压缩单个权重的方法

引言

这篇文章介绍一种不同于针对压缩单个权重的方法：多个权重数据组合为向量，将向量视为一个整体，映射到其他向量空间，完成压缩。作者在resnet-50上做了实验，将100MB权重压缩到了5MB（实现了20倍压缩比例），同时在imageNet上测试的top-1精度保持的很好（76.1%）。Resnet是一种经典的残差网络，在2015年的imageNet大赛中获得第一名，被广泛应用在图像识别和分类中。向量压缩方法在resnet上的成功运用，会大大推动resnet在硬件加速中的应用。 1

背景介绍

也许是神经网络较强的泛化能力和较窄的应用场景之间的矛盾，造成了网络参数存在很大冗余。因此各种压缩方法五花八门，层出不穷。

有的是将权重数据低精度化，比如前一篇介绍的二值网络，还有三值，四值网络，8bit，16bit定点网络等等。这些主要是考虑整体上降低每个权重的表达精度。但是随着精度降低越大，网络的分类能力就会越低。

另一类方法是向量量化。其主要思想是将原始高维权重空间分割成低维子空间的乘积，然后对子空间进行重新映射，通过映射到某个新的集合来完成整体数据的压缩。实际上是寻找不同向量之间的共性，用同一个新向量来替代，实现聚类。这样就减少了不同子向量的个数，实现了数据压缩。

还有一种方法是剪枝。即去除一些不重要的网络连接或者参数，比如在LSTM优化中使用的structured compression，就是直接去除多个相邻的不重要的权重参数。

利用以上的方法产生了多个压缩的网络结构，比如squeezeNet，NASNet，ShuffleNet，MobileNet等。这些网络是从网络结构的设计开始，就权衡数据量和分类精度，来实现既有小的权重数据，同时又有好的表现力。

2

压缩方法

这篇论文的创新性在于在采用向量压缩的基础上，最小化激活函数的输入而不是权重的均方差。相比于传统方法，其在测试集中有更好的分类能力，同时不需要任何监督过程，只是给出一定数量的输入图片就行了。

图2.1 绿色的线是论文的方法，在测试集和中有更好的分类能力，而传统方法会在压缩过程中引入噪声，造成分类精度的降低

论文首先从全连接的量化讲解，之后推广到卷积的压缩。假设一个全连接层有权重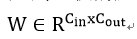： 将每列W分割成m个连续的子向量，然后让网络学习一个字典可以表示这mC_out个向量。子向量维度为d=C_in/m。假设字典有k个数据{C_1, C_2, …, C_k}。任何一个d维向量都被映射到这个空间中，于是一个W的列向量映射为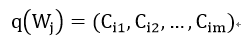： 这个字典是通过最小化权重的均方差来学习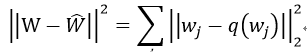： 从实际来讲，我们要减小的并不是权重之间的差异，而是结果的差异。所以论文从更直观的角度来最小化输出结果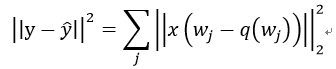： 其中，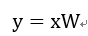

是全连接层的输出结果。

具体实现步骤为：

1） 为了匹配W子向量，输入x也进行相对应的分割。由BxC_inàBxmxd；

2） 对每个子W向量进行聚类，分配字典中的向量c：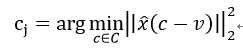

其中v是W的子向量，c为字典中向量。X^为x的子空间。

2） 更新字典数据c：假设对应c向量已经分配了一定数量的v，那么通过以下方法来更新c：

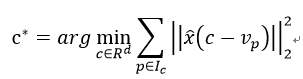全连接进行的是矩阵运算，而卷积层是由卷积核来实现图像的卷积。两者不同，如何将前面的方法用到卷积层呢？其实向量压缩算法本身不在做什么运算，而是在于对权重的重新分类。从这点来看，一个卷积层权重为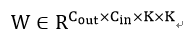： 其中KxK为一个卷积核大小，可以作为一个基本的子向量单位。我们可以选择拆分的W的字向量大小为hxKxK。如果h=1，那么一个卷积核就被当做一个要映射的子向量。而输出不再是矩阵乘法而是卷积运算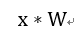： 这样就能够应用以上方法来对卷积层权重进行压缩了。

图2.2 卷积层权重数据进行KxK子空间分解

3

实验结果

论文在resnet-18和resnet-50上进行了实验。3x3卷积的子空间被设置为9或者18，而pointwise的权重子空间设置为4或者8.字典的大小设置了四种不同数量：256,512,1024,2048。在开始量化前，从训练集中随机取得1024幅图片作为量化输入，执行2节中的量化步骤。结果综合了存储减小和分类精度两方面，如下图所示： 图3.1 resnet-18和resnet-50的压缩比例

从图中看出，采用小的子空间和大的字典元素数目有更好的分类精度，但是压缩率低。在实际应用中可以根据需要来调节这些参数获得你期望的压缩率和识别精度。

图3.1 resnet-18和resnet-50的压缩比例

从图中看出，采用小的子空间和大的字典元素数目有更好的分类精度，但是压缩率低。在实际应用中可以根据需要来调节这些参数获得你期望的压缩率和识别精度。

图3.2 k=256下，两个网络的压缩率和top-1精确度

结论

本文介绍了一种利用向量压缩来降低复杂的神经网络的数据量的方法，通过resnet上的实验，能够看出这种方法相对于单纯的压缩单个权重，可以保持良好的精确度，同时能够获得一定压缩比例。

文献

1 Pierre Stock, A.J., R´emi Gribonval, Benjamin Graham, Herv´e J´egou, And the Bit Goes Down Revisiting the Quantization of Neural Networks. arXiv preprint, 2019.