引言
在CNN网络中卷积运算占据了最大的计算量,压缩卷积参数可以获得显著的硬件加速器的性能提升。在即将介绍的这篇论文中,作者就是通过张量的降维来降低卷积计算量的。作者通过CP分解将一个4D张量分解成多个低维度的张量,并且最后通过微调参数来提升网络精度。
1 原理
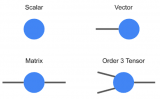
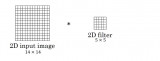
CNN卷积参数可以看做一个4D的张量。其中两个维度是对应一幅feature map的两个空间方向。一个方向对应输入feature map,另外一个维度为输出feature map方向。一个全卷积运算是对应每个输入feature map卷积求和,如图所示。通过CP分解,一个全卷积运算变成了连续多步一维卷积运算。图中S维度是多个输入feature map堆叠成的,dxd是feature map的空间维度。卷积核在feature map两个空间维度进行划窗运动,图中一个绿色方块内的结果求和得到一幅输出feature map中的一个像素点。T是多幅输出feature map堆叠成的。
那么这样的分解如何来保证和全卷积结果的不变呢?其实是要保证kernel不变就行了。然后再通过一些数学变化将全卷积变为连续多步卷积。已知一个二维矩阵可以进行如下分解:
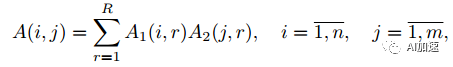
其中R是矩阵A的秩。计算量的降低取决于A的秩,秩越小,那么就可以被分解为更小矩阵,计算量降低的就越大。如果A的秩为其维度d,那么如果保持分解后秩不变,那么计算量是不能减小的,所以关键是看矩阵的秩的大小,秩的大小反映了网络的信息冗余度。将之推广到多维张量,有:

假设A张量维度为n1xn2x…nd,那么通过上述分解,参数量就大为降低,为(n1+n2+…nd)R个。
对于二维矩阵,可以使用SVD方式来计算分解的矩阵。但是当维数大于2,则无法使用这种方式了。作者选择了非线性最下平方差(non-linear least squares)方法,其通过降低L2项来获得分解矩阵。NLS方法计算的1维分解矩阵精度更好。
4D张量分解了,那么如何来将卷积计算分解为多步连续运算呢?一个全卷积运算表示为:

K为卷积核,维度为dxdxSxT。经过分解后卷积核为:
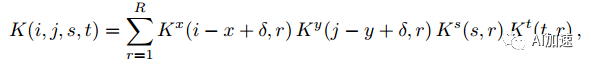
然后通过重新排序可以得到连续多步卷积运算:

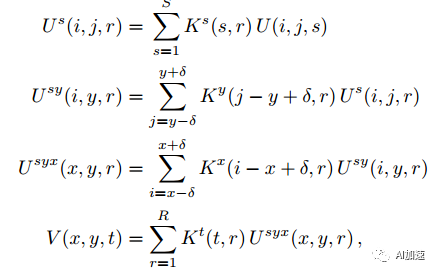
2 实验
在字符识别上,作者使用4层卷积网络,在不进行CP降维时,识别精度为91.2%。通过CP降维后,精度降低了1%,但是识别速率提升了8.5倍。
在ALEXNET网络上,CP降维实现了6.6倍速率提升,但是精度只降低了1%。
结论
CP分解降低了权重的秩,进而降低了计算量以及参数总量。多适用于小型的分类网络。
-
卷积
+关注
关注
0文章
95浏览量
18499 -
硬件加速器
+关注
关注
0文章
42浏览量
12756
原文标题:【网络压缩四】CP分解
文章出处:【微信号:FPGA-EETrend,微信公众号:FPGA开发圈】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
张量计算在神经网络加速器中的实现形式
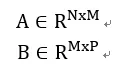
FFT与DFT计算时间的比较及圆周卷积代替线性卷积的有效性实
TensorFlow教程|张量的阶、形状、数据类型
卷积神经网络一维卷积的处理过程
降维空时自适应处理研究
融合朋友关系和标签的张量分解推荐算法
基于TTr1SVD的张量奇异值分解
谷歌宣布开源张量计算库TensorNetwork及其API
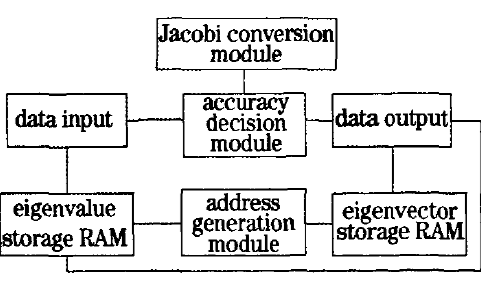
如何使用FPGA实现高光谱图像奇异值分解降维技术




 如何通过张量的降维来降低卷积计算量(CP分解)
如何通过张量的降维来降低卷积计算量(CP分解)











评论