介绍网络压缩算法，知识蒸馏

引言

学过化学的都知道蒸馏这个概念，就是利用不同组分的沸点不同，将不同组分从混合液中分离出来。知识蒸馏用于网络压缩，也具有类似的性质。具体的讲，有一个大的神经网络充当了“老师”的角色，她将书本上的知识先经过自己的转化和吸收，然后再传授给“学生”网络。学生网络模型相对较小，但是经过老师将知识提取教授，也可以实现大网络的功能。

知识蒸馏的方法是大名鼎鼎的Hinton提出的，这种方法实现了大网络向小网络的知识迁移，使得应用场景可以扩展到移动端。接下来我们具体看看知识蒸馏的整个过程。

1

原理

表面上看，大网络应该有更好的表达能力，或者说泛化能力。而小网络节点数量和大网络还有很大的差距，它如何能够做到逼近大网络的结果呢？首先，这与具体的应用场景范围有关，在一定的场景下，小网络可以接近大网络的分类能力。这就好像对于某个更复杂的函数，当限定某个值域的时候，可以用一些简单函数来逼近。其次，网络分类器最终的结果是用概率来表示的，分类结果取决于概率最大的。因此最大概率是90%和最大概率是60%的最终分类结果是一样的，这点就给了小网络更灵活的表达方式。最后就是小网络逼近大网络的程度和大网络的冗余程度有关，这类似于对大网络实行剪枝的结果。

那么如何训练一个小网络呢？我们可以先考虑一下在数值分析中，用一个函数S(x)来逼近另外一个函数f(x)，那么就可以通过最小化这两个函数在每个点的平方和来实现。同理，训练小的网络也必须使用大网络的输入和输出作为训练集，而不能再使用训练大网络的训练集了。原始训练集的标注结果是绝对的（是和不是：1,0），而大网络的输出结果是一个概率向量，其包含了每一类的概率大小。这个结果不再仅仅只含有原始训练集的信息，它还包含了大网络的信息。比如在原始图片中，一张猫的图片结果只有一个，但是经过大网络后，不仅仅有猫的结果，还有狗，房子，树等每个类别的概率结果。其他类别的概率实际上告诉了我们不同类别之间存在的差异和共性，比如一张猫的图片中是狗的概率可能就比是房子的概率大，因为猫和狗相对于猫和房子有更大的共性。

神经网络通常使用softmax函数来生成分类概率，这个函数形式为：

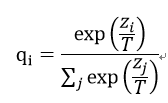
其中T是温度，通常设置为1。使用较高的T可以产生更加softer的概率分布。更softer的概率分布提高网络的泛化能力，有利于小网络的训练。

写到这里小编对softmax函数感到好奇，为什么神经网络都采用softmax来进行概率计算呢？学过热力学的会发现，这个softmax函数非常类似不同能级上粒子分布概率，位于能级E的粒子分布概率就是正比于：

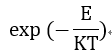
而且温度越高高能级粒子概率也越大，这与softmax函数也有同样的结果。其实观察他们的推导过程就会发现，它们之所以有相同的形式来自于它们都是多分类问题，而且概率模型都属于广义线性模型。Softmax函数正是在广义线性函数的假设上推导出来的。现在我们给出其传统推导，和基于热力学统计的推导方法。

首先看什么是广义线性模型，广义线性模型是用于处理条件概率的一个基本模型，很多常见的分布模型（伯努利，高斯等）都属于广义线性模型。定义线性预测算子：

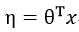
定义y基于x的条件概率分布，这个分布就是广义线性模型：

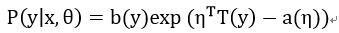
分类问题就是求在给定输入x的条件下，估计y值，即y属于哪个类的问题。可以通过期望值来作为y的估计。容易得到这个期望值为：

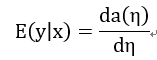
因此一旦知道y的概率分布就知道了y的估计。这个估计就是回归函数。现在我们来看softmax的传统推导。

Y有多个可能的分类：

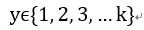
每种分类对应着概率：

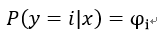
定义：

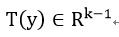
其中有：

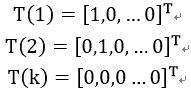
于是得到广义分布：

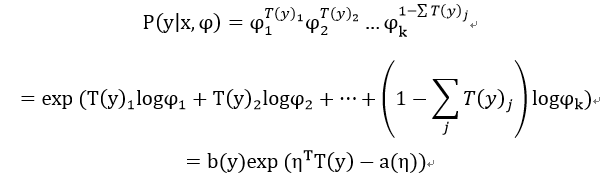
其中有，

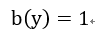
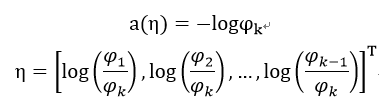
然后可以求出：

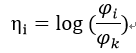
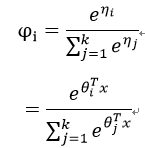
求得估计值：

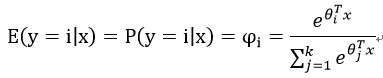
这就是softmax函数。

现在我们从统计热力学角度来推导softmax函数。

神经网络的作用是对输入进行特征提取，我们可以把这个提取过程表示为：

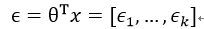
现在我们需要来理解E_i，这个应该是表示从属于特征i的程度，我们可以选择一定函数f(E_i)来作为评价属于特征i的程度。现在我们假设特征1到k是可以涵盖所有输入的，即任何输入都是由这些特征构成的，特征值反应了输入属于某个特征的量，那么所有这些特征的量之和应该是所有输入量的和，那么我们可以有：

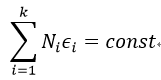
我们现在需要求y属于这个特征的概率，即：

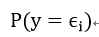
现在我们假设有N个数，这些数要分配不同的y值。这些数被分配是完全随机的，但是受到每种y值的数量限制，对应E_i的数量为N_i。那么将这N个数分配给k个不同类的分配方式可以得到：

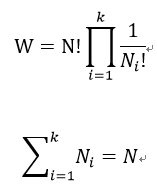
我们来最大化W，即求最大似然函数：

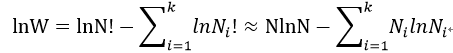
满足约束条件：

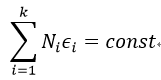
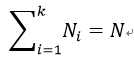
我们利用拉格朗日对偶原理来求解极值：

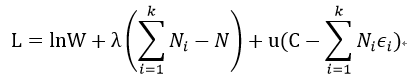
我们可以得到类似玻尔兹曼分布的公式：

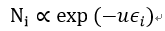
其中u就是温度1/T。

现在回到正题，过于softer的代价函数可能会造成分类结果错误率低，为了平衡分类错误和小模型泛化能力，hinton提出使用两个代价函数来进行训练，一个是T值较大，另外一个是T值为1。通过调节这两个代价函数的比例来获得满意的训练结果。

2

实验结果

Hinton的论文中分别在MINIST，语音识别上进行了实验。我们仅仅看一下实验结果，对知识蒸馏效果有个简单印象。更深入的理解离不开实践，只有真正去写代码去看结果，才能不会纸上谈兵。

1） MINIST

大网络含有2个隐含层，1200个激活单元，60000个训练集图片。作者通过剪枝来将大网络减小到只有800个激活单元，将温度增加到20，相比于没有regularization会减小很大错误率。

2） 语音识别

这里作者使用多个小网络集合来作为教师网络，然后单个网络作为学生网络。每个网络为8个隐含层，2560个激活单元，训练集有14000个标注数据。结果如下：

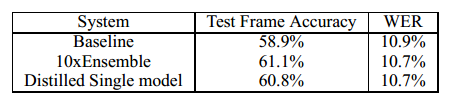
其中WER为错误率。

总结

本文介绍了网络压缩算法，知识蒸馏。很多是小编个人理解，如有不同意见欢迎指正交流。更多可以参考hinton大神的知识蒸馏文献。