正弦交流电的表示法
正弦交流电的三种表示法一般有四种表示方法:解析法、曲线法、旋转矢量法和符号法。
这里介绍前三种表示法:
(1)解析法:又称三角函数表示法,是正弦交流电的基本表示方法。它就是用三角函数式来表示正弦交流电随时间变化的关系。
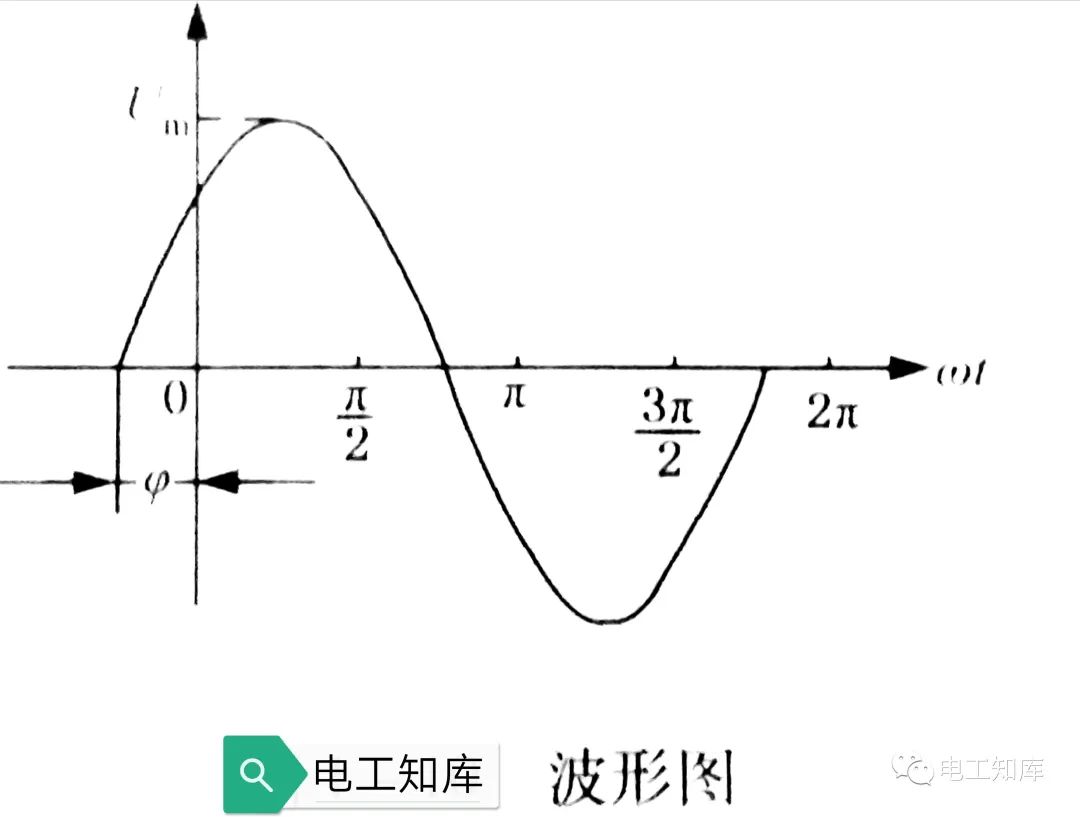
(2)曲线法:就是利用三角函数式求出个时刻的相应角和对应的瞬时值,然后在平面直角坐标系中画出正弦曲线。又叫曲线图或波形图。
(3)旋转矢量法:在数学中,我们已知道一个既有大小、又有方向的量,叫做矢量,而当一个矢量,以角速度绕点作反时针方向旋转时,我们则称它为旋转矢量。
正弦交流电的三要素
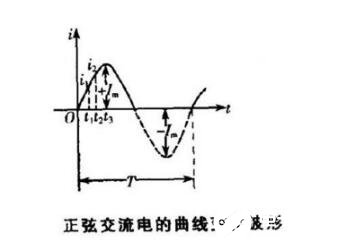
(一)最大值(也称为峰值或幅值),Em、Um、Im
最大值就是最大的瞬时值。在一个周期内必然出现一个正值和一个负值两次。
(二)角频率(ω)
通常把正弦交流电在任一瞬间所处的角度称为电角度,每变化一周的电角度为360°,也称为2π弧度(rad)。角频率是正弦交流电在秒钟内变化的弧度,用符号表示,单位为弧度/秒,用符号rad/s表示。因为交流电一周的弧度是2π,所以频率为f的交流电,在一秒内变化的弧度为2πf,角频率可表示为:ω=2πf
(三)初相位与相位差 φ、φ1-φ2
初相位就是正弦量在起始时间的相位。在波形图上,初相位规定为正半波的起点与坐标原点之间的夹角。当φ=0时,正半波起点正好落在原点O上;当φ>0时,则正半波起点在原点O的左边;当φ<0时,正半波起点在原点O的右边。
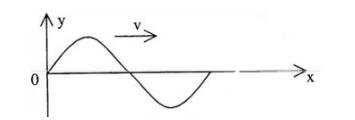
相位差是指两个同频率正弦量的相位(或初相位)之差。两个同频率正弦交流电的相位差与时间无关。所以,不同频率的两个正弦量,讨论它们间的相位差是没有意义的。
在分析交流电路时,常需要比较几个不同频率的正弦量之间的相位关系,此时,可任选一个正弦量的初相位零作参考正弦量,其它各量则可按与参考正弦量的相位差来确定其初相,但讨论过程中不可变更。
-
交流电
+关注
关注
14文章
677浏览量
34490 -
正弦交流电
+关注
关注
0文章
32浏览量
11642
发布评论请先 登录
相关推荐
什么是正弦交流电?什么是市电?

单相正弦交流电的是如何产生的和正弦交流电的公式详细资料概述
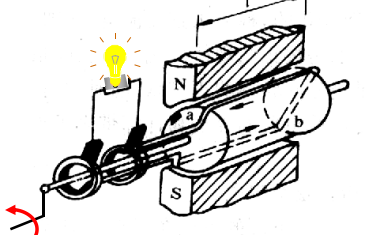





 正弦交流电的表示方法
正弦交流电的表示方法











评论