读懂NeurIPS2019最佳机器学习论文

引言

NeurIPS是全球顶级的机器学习会议。没有其他研究会议可以吸引6000多位该领域内真正的精英同时参加。如果你非常想了解机器学习最新的研究进展，就需要关注NeurIPS。

每年，NeurIPS都会为机器学习领域的顶级研究论文颁发各类奖项。考虑到这些论文的前沿水平，它们对于大多数人来说通常晦涩难懂。

但是不用担心！我浏览了这些优秀论文，并在本文总结了要点！我的目的是通过将关键的机器学习概念分解为大众易于理解的小点来帮助你了解每篇论文的本质。

以下是我将介绍的三个NeurIPS2019最佳论文的奖项：

最佳论文奖

杰出新方向论文奖

经典论文奖

让我们深入了解吧！

NeurIPS 2019最佳论文奖

在NeurIPS 2019上获得的最佳论文奖是：

具有Massart噪声的半空间的独立分布的PAC学习（Distribution-Independent PAC Learning of Halfspaces with MassartNoise）

这是一篇非常好的论文！这让我开始思考机器学习中的一个基本概念：噪声和分布。这需要对论文本身进行大量研究，我将尽力解释论文的要点而不使其变得复杂。

我们先重述标题。本文的研究讨论了一种用于学习半空间的算法，该算法在与分布无关的PAC模型中使用，且研究的半空间具有Massart噪声。该算法是该领域中最有效的算法。

本文的关键术语如下。

回顾布尔函数和二进制分类的概念。本质上，

一个半空间是一个布尔函数，其中两个类（正样本和负样本）由一个超平面分开。由于超平面是线性的，因此它也被称为线性阈值函数（LTF）。

在数学上，线性阈值函数或半空间是一个阈值函数，可以由以某个阈值T为边界的输入参数的线性方程表示。布尔函数如果具有以下形式，则为线性阈值函数：

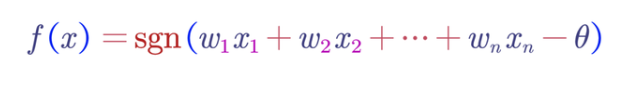
其中：

是权重

是特征

表示给出实数符号的符号函数

是阈值

我们也可以将LTF称为感知器（此处需要使用神经网络知识！）。

PAC（Probably Approximately Correct）模型是二分类的标准模型之一。

“Massart噪声条件，或仅仅是Massart噪声，是每个样本/记录的标签以学习算法未知的很小概率进行的翻转。”

翻转的可能性受某个始终小于1/2的因子n的限制。为了找到使得误分类错误较小的假设，我们在先前的论文中进行了各种尝试来限制错误以及与数据噪声相关的风险。

这项研究在确定样本复杂性的同时，证明了多项式时间（1/epsilon）的额外风险等于Massart噪声水平加上epsilon。

本文是迈向仅实现ε过量风险这一目标的巨大飞跃。

获得NeurIPS杰出论文奖提名的其他论文：

1. Besov IPM损耗下GAN的非参数密度估计和收敛速度（Nonparametric Density Estimation & Convergence Rates for GANs under Besov IPM Losses）

2. 快速准确的最小均方求解（Fast andAccurate Least-Mean-Squares Solvers）

NeurIPS 2019杰出新方向论文

今年的NeurIPS2019为获奖论文设置了一个新奖项杰出新方向论文奖。用主办方的话来说： “该奖项旨在表彰为未来研究建立新途径的杰出工作。”

该奖项的获奖文章是 ——《一致收敛性可能无法解释深度学习中的泛化性》（Uniform convergence may be unable to explain generalization in deeplearning）

今年我最喜欢的论文之一！本文从理论和实践两个方面阐述了当前的深度学习算法无法解释深度神经网络中的泛化。让我们来更详细地了解这一点。

一致收敛性可能无法解释深度学习中的泛化性（Uniform convergence may be unable to explain generalization in deeplearning）

大型网络很好地概括了看不见的训练数据，尽管这些数据已被训练为完全适合随机标记。但是，当特征数量大于训练样本的数量时，这些网络的表现就没那么好了。

尽管如此，它们仍然为我们提供了最新的性能指标。这也表明这些超参数化模型过度地依赖参数计数而没有考虑批量大小的变化。如果我们遵循泛化的基本方程：

测试误差 – 训练误差 《= 泛化界限

对于上面的方程式，我们采用所有假设的集合，并尝试最小化复杂度并使这些界限尽可能地窄。

迄今为止的研究都集中于通过获取假设类别的相关子集来收紧界限。在完善这些约束方面也有很多开创性的研究，所有这些都基于统一收敛的概念。

但是，本文解释这些算法可能出现的两种情况：

太大，并且其复杂度随参数数量而增加；

很小，但是在修改后的网络上设计而来

“该论文定义了一组用于泛化界限的标准，并通过一组演示实验证明统一收敛为何无法完全解释深度学习中的泛化。”

泛化界限如下：

1. 理想情况下必须 《1（空）

2. 随着宽度的增加变小

3. 适用于由SGD（随机梯度下降）学习的网络

4. 随着随机翻转的训练标签的比例而增加

5. 应该与数据集大小成反比

之前提到的实验是在MNIST数据集上使用三种类型的过度参数化模型（均在SGD算法上进行训练）完成的：

1. 线性分类器

2. 具有ReLU的宽神经网络

3. 具有固定隐藏权重的无限宽度神经网络

本文继而演示了针对不同训练集大小的不同超参数设置。

“一个非常有趣的发现是，尽管测试集误差随训练集大小的增加而减小，但泛化界限实际上却有所增加。 ”

如果网络只是记住了我们不断添加到训练集中的数据点，该怎么办？

以研究人员给出的例子为例。对于一个拥有1000个维度的数据集的分类任务，使用SGD训练具有1个隐藏层ReLU和10万个单位的超参数化模型。训练集大小的增加可提高泛化性并减少测试集错误。

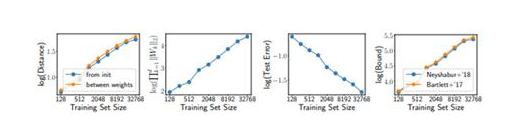
尽管进行了泛化，它们仍然证明了决策边界非常复杂。这是它们违背统一收敛思想的地方。

因此，即使对于线性分类器，统一收敛也不能完全解释泛化。实际上，当增加样本数量时，这可以认为是导致界限增加的一个因素！

尽管先前的研究已将发展深度网络的方向朝着依赖于算法的方向发展（以便坚持一致收敛），但本文提出了开发不依赖于算法的技术的需求，这些技术不会局限于一致收敛来解释泛化。

我们可以清楚地知道，为什么该机器学习研究论文在NeurIPS 2019上获得了杰出新方向论文奖。

研究人员已经表明，仅仅用一致收敛不足以解释深度学习中的泛化。同样，不可能达到满足所有5个标准的小界限。这开辟了一个全新的研究领域来探索可能解释泛化的其他工具。

NeurIPS在杰出新方向论文奖上的其他提名包括：

1. 端到端：表征的梯度隔离学习（Putting AnEnd to End-to-End： Gradient-Isolated Learning of Representations）

2. 场景表示网络：连续的3D-结构感知神经场景表示（SceneRepresentation Networks： Continuous 3D-Structure-Aware Neural SceneRepresentations）

NeurIPS 2019的经典论文奖

每年，NeurIPS还会奖励10年前在大会上发表的一篇论文，该论文对该领域的贡献产生了深远的影响（也是广受欢迎的论文）。

今年，“经典论文奖”授予了LinXiao写作的“正则随机学习和在线优化的双重平均法”。这项研究基于基本概念，这些基本概念为众所周知的现代机器学习奠定了基础。

正则随机学习和在线优化的双重平均法（Dual Averaging Method for Regularized Stochastic Learning and OnlineOptimization）

让我们分解一下这篇极佳的论文中涵盖的四个关键概念：

随机梯度下降：随机梯度下降已经正式成为机器学习中的最优化方法。它可以通过以下随机优化来实现。回顾SGD和大样本随机优化方程——这里，w是权重向量，z是输入特征向量。对于t = 0，1，2…

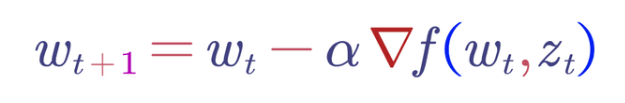
在线凸优化：另一项开创性的研究。它被模拟为游戏，玩家将尝试预测权重向量，并在每个t处计算出最终的损失。主要目的是最大程度地减少这种损失——结果与我们使用随机梯度下降进行优化的方式非常相似

压缩学习：这包括套索回归，L1正则化最小二乘和其他混合正则化方案

近端梯度法：与早期的技术相比，这是一种减少损耗且仍保留凸度的更快的方法

尽管先前的研究开发了一种收敛到O（1/t）的有效算法，但数据稀疏性是在那之前一直被忽略的一个因素。本文提出了一种新的正则化技术，称为正则化双重平均法（RDA），用于解决在线凸优化问题。

当时，这些凸优化问题效率不高，特别是在可伸缩性方面。

这项研究提出了一种批处理优化的新方法。这意味着最初仅提供一些独立样本，并且基于这些样本（在当前时间t）计算权重向量。相对于当前权重向量的损失与次梯度一起计算。并在迭代中（在时间t + 1）再次使用它。

具体而言，在RDA中，考虑了平均次梯度，而不是当前的次梯度。

“当时，对于稀疏的MNIST数据集，此方法比SGD和其他流行技术获得了更好的结果。实际上，随着稀疏度的增加，RDA方法也具有明显更好的结果。”

在进一步研究上述方法的多篇论文中，如流形识别、加速RDA等，都证明了这篇论文被授予经典论文奖是当之无愧。

结语

NeurIPS 2019再次成为了一次极富教育意义和启发性的会议。我对杰出新方向论文奖以及它如何解决深度学习中的泛化问题特别感兴趣。

哪一篇机器学习研究论文引起了你的注意？或者是否有其他的论文，让你想要去尝试或者启发了你？请在下面的评论区中告诉我们吧。