机器学习的回归分析和回归方法

根据受欢迎程度，线性回归和逻辑回归经常是我们做预测模型时，且第一个学习的算法。但是如果认为回归就两个算法，就大错特错了。事实上我们有许多类型的回归方法可以去建模。每一个算法都有其重要性和特殊性。

内容

1.什么是回归分析？

2.我们为什么要使用回归分析？

3.回归有哪些类型 ？

4.线性回归

5.逻辑回归

6.多项式回归

7.逐步回归

8.岭回归

9.Lasso回归

10.ElasticNet回归

什么是回归分析？

回归分析是研究自变量和因变量之间关系的一种预测模型技术。这些技术应用于预测，时间序列模型和找到变量之间关系。例如可以通过回归去研究超速与交通事故发生次数的关系。

我们为什么要用回归分析？

这里有一些使用回归分析的好处：它指示出自变量与因变量之间的显著关系；它指示出多个自变量对因变量的影响。回归分析允许我们比较不同尺度的变量，例如：价格改变的影响和宣传活动的次数。这些好处可以帮助市场研究者／数据分析师去除和评价用于建立预测模型里面的变量。

回归有哪些类型？

我们有很多种回归方法用预测。这些技术可通过三种方法分类：自变量的个数、因变量的类型和回归线的形状。

1.线性回归

线性回归可谓是世界上最知名的建模方法之一，也是应该是我们第一个接触的模型。在模型中，因变量是连续型的，自变量可以使连续型或离散型的，回归线是线性的。

线性回归用最适直线（回归线）去建立因变量Y和一个或多个自变量X之间的关系。可以用公式来表示：

Y=a+b*X+e

a为截距，b为回归线的斜率，e是误差项。

简单线性回归与多元线性回归的差别在于：多元线性回归有多个（》1）自变量，而简单线性回归只有一个自变量。到现在我们的问题就是：如何找到那条回归线？

我们可以通过最小二乘法把这个问题解决。其实最小二乘法就是线性回归模型的损失函数，只要把损失函数做到最小时得出的参数，才是我们最需要的参数。

我们一般用决定系数（R方）去评价模型的表现。

重点：

1.自变量与因变量之间必须要有线性关系。

2.多重共线性、自相关和异方差对多元线性回归的影响很大。

3.线性回归对异常值非常敏感，其能严重影响回归线，最终影响预测值。

4.在多元的自变量中，我们可以通过前进法，后退法和逐步法去选择最显著的自变量。

2. 逻辑回归

逻辑回归是用来找到事件成功或事件失败的概率。当我们的因变量是二分类（0/1，True/False，Yes/No）时我们应该使用逻辑回归。

重点：

1.在分类问题中使用的非常多。

2.逻辑回归因其应用非线性log转换方法，使得其不需要自变量与因变量之间有线性关系。

3.为防止过拟合和低拟合，我们应该确保每个变量是显著的。应该使用逐步回归方法去估计逻辑回归。

4.逻辑回归需要大样本量，因为最大似然估计在低样本量的情况下表现不好。

5.要求没有共线性。

6.如果因变量是序数型的，则称为序数型逻辑回归。

7.如果因变量有多个，则称为多项逻辑回归。

3. 多项式回归

如果一个回归，它的自变量指数超过1，则称为多项式回归。可以用公式表示：

y = a + b * x^2

在这个回归技术中，最适的线不是一条直线，而是一条曲线。

重点：

① 很多情况下，我们为了降低误差，经常会抵制不了使用多项式回归的诱惑，但事实是，我们经常会造成过拟合。所以要经常的把数据可视化，观察数据与模型的拟合程度。

② 特别是要看曲线的结尾部分，看它的形状和趋势是否有意义。高的多项式往往会产生特别古怪的预测值。

4. 逐步回归

当我们要处理多个自变量时，我们就需要这个回归方法。在这个方法中选择变量都是通过自动过程实现的，不需要人的干预。

这个工程是通过观察统计值，比如判定系数，t值和最小信息准则等去筛选变量。逐步回归变量一般是基于特定的标准加入或移除变量来拟合回归模型。

一些常用的逐步回归方法如下：

1. 标准逐步回归做两件事情。只要是需要每一步它都会添加或移除一些变量。

2. 前进法是开始于最显著的变量然后在模型中逐渐增加次显著变量。

3. 后退法是开始于所有变量，然后逐渐移除一些不显著变量。

4. 这个模型技术的目的是为了用最少的变量去最大化模型的预测能力。它也是一种降维技术。

5. 岭回归

当碰到数据有多重共线性时，我们就会用到岭回归。所谓多重共线性，简单的说就是自变量之间有高度相关关系。在多重共线性中，即使是最小二乘法是无偏的，它们的方差也会很大。通过在回归中加入一些偏差，岭回归酒会减少标准误差。

‘岭回归是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。’ －－－百度百科

岭回归是通过岭参数λ去解决多重共线性的问题。看下面的公式：

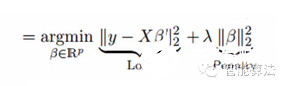
其中loss为损失函数，penalty为惩罚项。

重点：

1.岭回归的假设与最小二乘法回归的假设相同除了假设正态性。

2.它把系数的值收缩了，但是不会为0.

3.正则化方法是使用了l2正则。

6. LASSO回归

和岭回归类似，Lasso（least Absolute Shrinkage and Selection Operator）也是通过惩罚其回归系数的绝对值。看下面的公式：

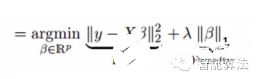
Lasso回归和岭回归不同的是，Lasso回归在惩罚方程中用的是绝对值，而不是平方。这就使得惩罚后的值可能会变成0.

重点：

1.其假设与最小二乘回归相同除了正态性。

2.其能把系数收缩到0，使得其能帮助特征选择。

3.这个正则化方法为l1正则化。

4.如果一组变量是高度相关的，lasso会选择其中的一个，然后把其他都变为0.

7. ElasticNet回归

ElasticNet回归是Lasso回归和岭回归的组合。它会事先训练L1和L2作为惩罚项。当许多变量是相关的时候，Elastic-net是有用的。Lasso一般会随机选择其中一个，而Elastic-net则会选在两个。

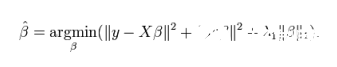
与Lasso和岭回归的利弊比较，一个实用的优点就是Elastic-Net会继承一些岭回归的稳定性。

重点：

1.在选择变量的数量上没有限制

2.双重收缩对其有影响

3.除了这7个常用的回归技术，你也可以看看贝叶斯回归、生态学回归和鲁棒回归。

如何选择回归模型？

面对如此多的回归模型，最重要的是根据自变量因变量的类型、数据的维数和其他数据的重要特征去选择最合适的方法。以下是我们选择正确回归模型时要主要考虑的因素：

1.数据探索是建立预测模型不可或缺的部分。它应该是在选择正确模型之前要做的。

2.为了比较不同模型的拟合程度，我们可以分析不同的度量，比如统计显著性参数、R方、调整R方、最小信息标准、BIC和误差准则。另一个是Mallow‘s Cp准则。

3.交叉验证是验证预测模型最好的方法。你把你的数据集分成两组：一组用于训练，一组用于验证。

4.如果你的数据集有许多让你困惑的变量，你就不应该用自动模型选择方法，因为你不想把这些变量放在模型当中。

5.不强大的模型往往容易建立，而强大的模型很难建立。

6.回归正则方法在高维度和多重共线性的情况下表现的很好。