矢量运算在磁场中的应用

我们知道，磁感应强度是一种矢量，所以在存在多个磁场的空间区域内，复合磁场的计算需要用到矢量运算的知识。

我们以一道奥赛真题为例来说明矢量运算在磁场中的应用。

例空间某区域内存在两个匀强磁场，其中一个匀强磁场B1的方向平行纸面向右，磁感应强度B1=1T，长L=1m的直导线通有I=1A的恒定电流，当导线平行于纸面与B1成60度夹角时，其所受到的安培力为0，而将导线垂直于纸面放置时，测得其所受到的安培力大小为2N，求另一匀强磁场B2的磁感应强度大小。

分析：一般情况下，通电导线在磁场中将受到安培力的作用，那什么时候受力为0呢？只有在导线与磁感应强度的方向平行的时候才不受力。所以B1与B2的合磁感应强度B与导线的夹角应该0度或者180度，并且平行于纸面，画出磁感应强度的矢量图如下。

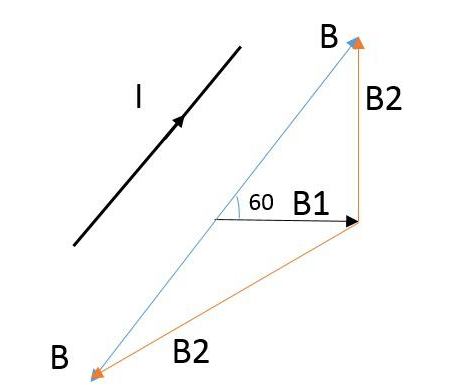
而当导线垂直于纸面时显然导线也垂直于合磁感应强度B，此时导线所受的安培力

F=BIL=2N，解得B=2T

已知B和B1的两个矢量的大小和方向，运用矢量加减法的规则和余弦定理即可求出B2的大小为

B2=√3T或者√7T，方向如图中红线标示。

考察点：

1、安培力方向、磁场方向和电流方向三者之间的关系（左手定则）；

2、矢量合成（矢量相加与矢量相减）；

3、三角公式余弦定理的运用。