线性回归是人工智能机器学习里面最基础的算法

线性回归是人工智能机器学习里面最基础的算法。

回归概念

在介绍线性回归之前先介绍下什么是回归。回归这个概念要追溯到19世纪，最早是由高尔顿提出的，高尔顿是达尔文的表弟，他非常崇拜达尔文，他一生最著名的发现是父辈身高和字辈身高的关系。按照我们日常经验，高个子的父辈子女也是高个子，矮个子的父辈子女也是矮个子，但大家并没有发现另外一个规律，就是高个子的父辈子女平均身高要比父辈低，矮个子父辈身高比父辈高，这个叫做‘回归’平庸，他认为自然界有一种约束力，使得身高的分布不会向高矮两个极端发展，而是趋于回到中心，所以称为回归。

在我们机器学习中的回归其实就是从样本数据中找到一个数学模型，找到事物的客观存在的规律。

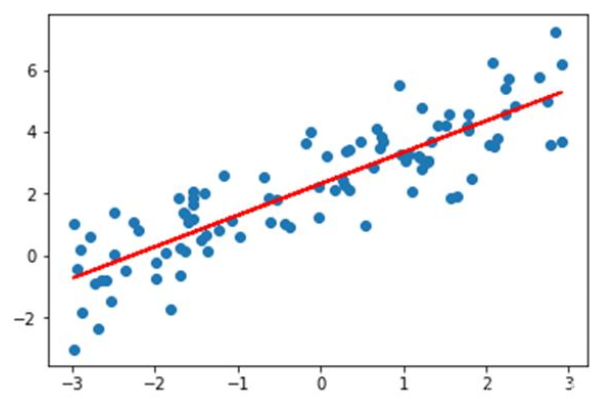
如上图所示，蓝色的点为样本点，假设x轴是房屋面积，y轴是房屋价格，那线性回归就是找到这样一条红色的直线，使得它对所有的样本做出做好的拟合，也就是距离所有的样本点平均距离最近，这样当有新的房屋面积需求时候，估计出来的房屋价格误差就是最小的。

原理

我们上面看到了，要拟合一条直线符合样本规律，则需要样本到这条直线的平均距离最近。那怎么计算这个平均距离呢？

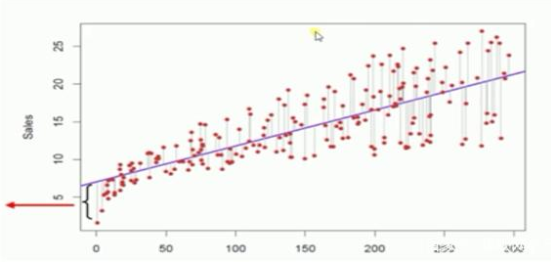
上图所示，我们就计算每个样本点到这条直线的‘垂直距离’，注意，是垂直距离，不是点到直线的距离，就是从样本点向直线做一条平行于y轴的直线。大家看上图就很快明白。

那这个距离怎么计算呢？这个就需要使用我们中学学过的几何知识了。

二维坐标下直线的方程为

我们就是求w1和w2 使得每个样本点到这条直线的平均距离最短

假设样本点的坐标为（xi，yi）i=1-n，我们总共有n个样本点。

那所有的样本最短就要把所有点到直线的距离差计算出来，然后平方（消除负号，当然求绝对值也可以，但计算更加繁琐）

得到下面公式

这个公式被称为线性回归的损失函数，参数是 w0 和w1，yi和xi为样本数据。我们要求这个公式的最小值。

这个公式的最小值可以对w0 和w1 分别求导数，得到下面公式

这个是一个二元一次方程可以解出来w0和w1的值。这就是最小二乘法的解法。

梯度下降法

上面的解法虽然能够解出来w0和w1，但计算量很大，容易出错。在工程上更多是使用梯度下降法进行计算。

如上图所示，梯度下降法就是从一个起始点出发，不断的试错，就像闭眼睛下山一样，每次都下降一小步，沿着下降最快的方向，也就是梯度最大的方向，不断的这样迭代，一直到下降的高度到达一个很小的值，就认为到底谷底了。对凸函数来说，梯度下降法找的极值点就是全局极值点。

梯度下降法是一个迭代算法，主要是找到梯度下降的最大的方向，每次下降的步长是需要程序员自己设置的。如果设置得过大，会导致算法震荡，如果过小则收敛速度太慢。如下图的是步长过大跳过了极值点

梯度下降法的计算过程：

α是梯度下降法的步长，两个式子分布是对w0和w1求偏导数。