现代设备故障的6种形式及应对策略

一个复杂的系统或设备是由许多不同零部件构成的，如果这些零部件发生故障（失效），可能导致整个系统发生故障。现代设备的复杂化使得故障模式呈多样化趋势，设备故障率随时间的发展规律主要有6种形式。

1.浴盆曲线

研究故障宏观统计规律主要是研究故障率随时间变化的规律。在一段时间内，具有代表性的是浴盆曲线，如图1所示。

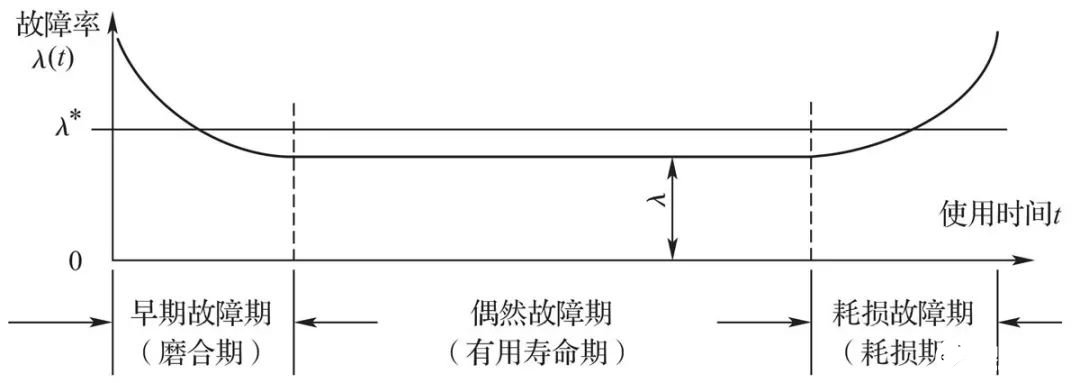
图1 浴盆曲线

从图1可以看出，在一个复杂系统或设备的寿命周期中，故障率随时间的变化分为三个阶段：早期故障期、偶发故障期和耗损故障期。

①早期故障期的故障主要由设计、制造和材质上的缺陷或操作不熟练等原因造成，发生在设备的使用初期、大修理或改造后使用初期；开始故障率较高，随着故障的排除，故障率逐渐下降了。

②偶发故障期的故障主要由构成系统、设备和零部件的某些无法预测的缺陷所引起。在此期间，故障不可预测，不受运转时间的影响而随机发生。此时期的故障率λ（t）基本保持不变，且服从指数分布。这一时期是设备的最佳工作期。

③耗损故障期的故障主要由构成设备的大部分零部件集中耗损而产生，其表现形式是随着运转时间的增加，故障率逐渐升高。

通常，根据设备的耗损故障情况和能力，制定一条“容许的故障率λ∗”的界线，以控制实际故障率不超过此范围。维修人员的工作是努力延长设备寿命，减少停机时间，降低故障率，使其不超过规定的“容许的故障率λ∗”界线。

2.一般设备故障率曲线的基本形式

通过美国航空航天局（NASA）统计数据表明，航空设备故障率大致可以分为六种类型，其故障率曲线如图2所示。

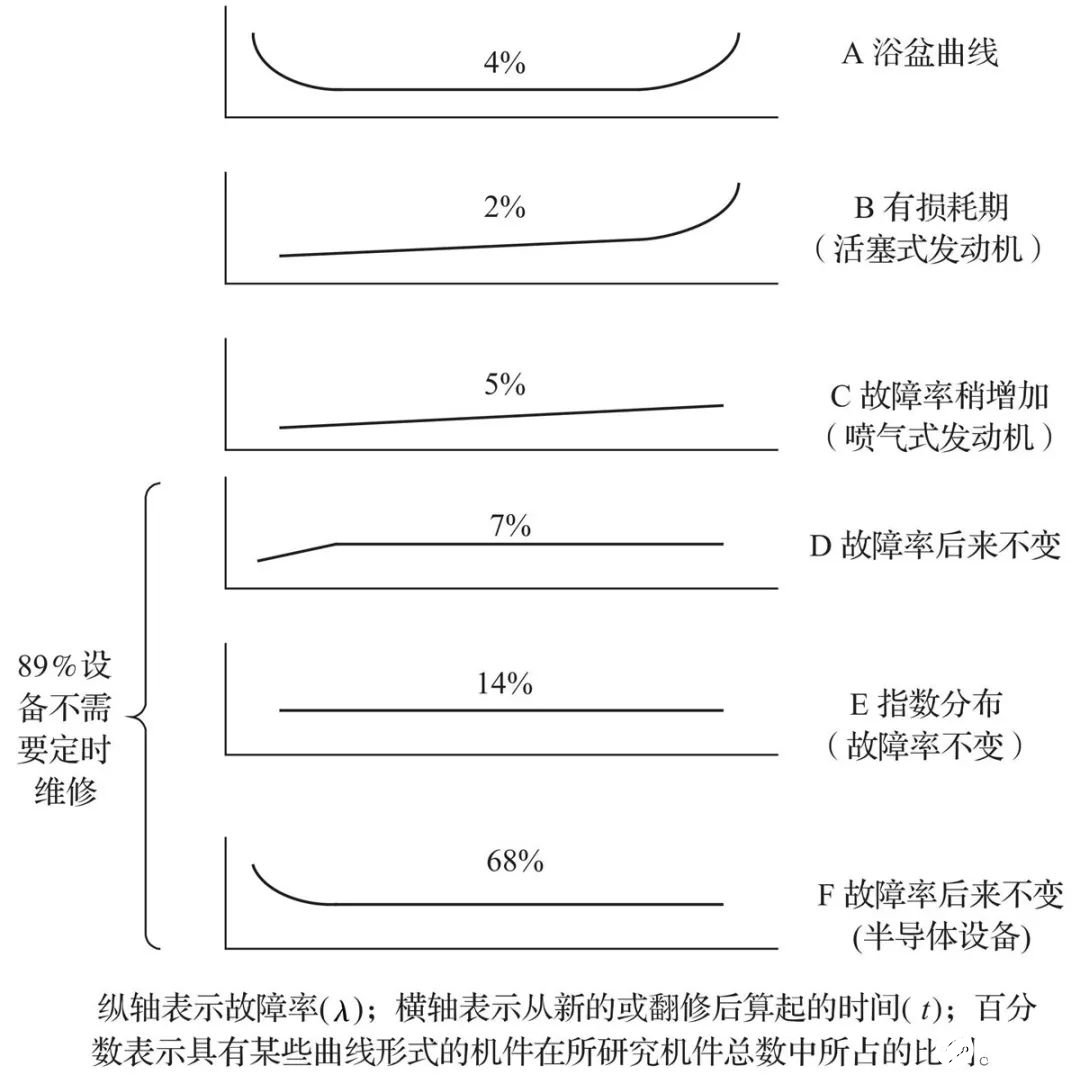
图2 六种基本故障率（λ）与时间（t）的关系曲线

对于图2中的六种故障率曲线，可以看到，A型为经典的浴盆曲线，有明显的耗损期；B型故障率具有常数或渐升的特征，然后出现明显的耗损期，符合这两种形式的是各种零件或简单产品的故障，如轮胎、刹车片、活塞式发动机的汽缸的故障，它们通常具有机械磨损、材料老化、金属疲劳等；C型没有明显的耗损期，但是故障率也是随着使用时间的增加而增加的；曲线D显示了新设备从刚出厂的低故障率，急剧地增长到一个恒定的故障率；曲线E显示设备的故障为恒定值，出现的故障常常是偶然因素造成的；而曲线F显示设备开始有高的初期故障率，然后急剧下降到一个恒定的或者是增长极为缓慢的故障率。

具有A、B型耗损特性的航空设备仅占全部设备的6%，具有经典浴盆曲线（A型）的仅占4%，没有明确耗损期（C型）的占5%，以上三种形式故障率的设备共占11%。而89%的设备则没有耗损期（D、E、F型），归为E型，这些不需要定时维修。

一般来说，在实际运行中，设备的故障率应该是图中所示的六种曲线中的一种或几种的合成（浴盆曲线可以看作曲线B、E和F的合成），其故障率可能与民用飞机的故障率不完全相同。但是，设备故障率取决于设备的复杂性，设备越复杂，其故障曲线越是接近于曲线E和F。

A、B、C、E四种曲线的分布函数及其故障率模型和维修策略简述如下。

①浴盆曲线（曲线A）：浴盆曲线的分布函数为

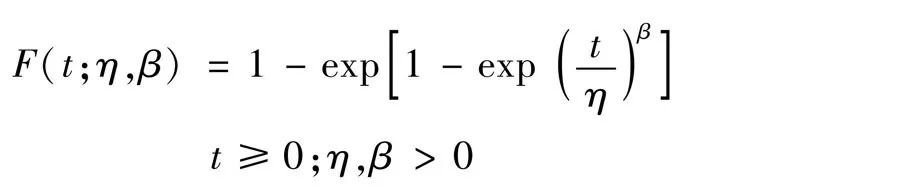
相应的密度函数为

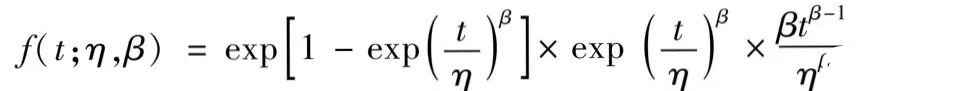
这是一个两参数模型，其失效率函数为

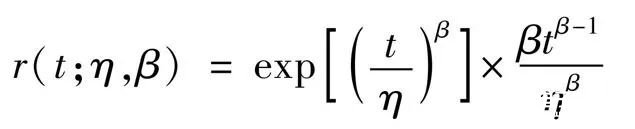
这里，故障率函数r（t）可以看作两个函数r1（t; η， β）和r2（t; η， β）的乘积。其中，当β＜1时，r1为减函数，而r2则总是增函数。

r（t）的导数表示为

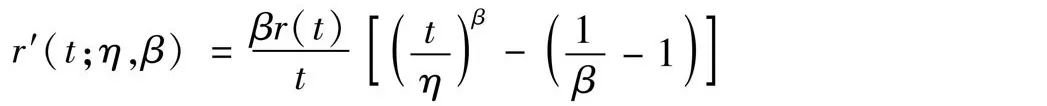
由上式知：当β＜1时，r（t）是浴盆曲线形状，其最低点对应的t值为

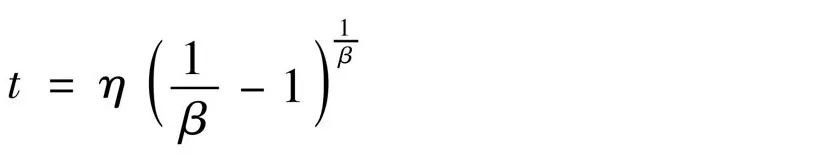
浴盆曲线的维修策略为：对于早期故障，只能在发现故障后立即采取排除措施，不适于采取定时更换的事前预防对策。因为在早期故障率高的情况下，如果企图以新品更换在用品，就等于用故障率高的机件更换故障率低的机件，不仅不能降低总的故障率，反而会产生相反的效果。

图3表示每相隔间隔期T实行定时更换时故障率的变化情况。每次定时更换，都会使故障率升高，并使平均故障率大于λ（T），保持在相对较高的水平。

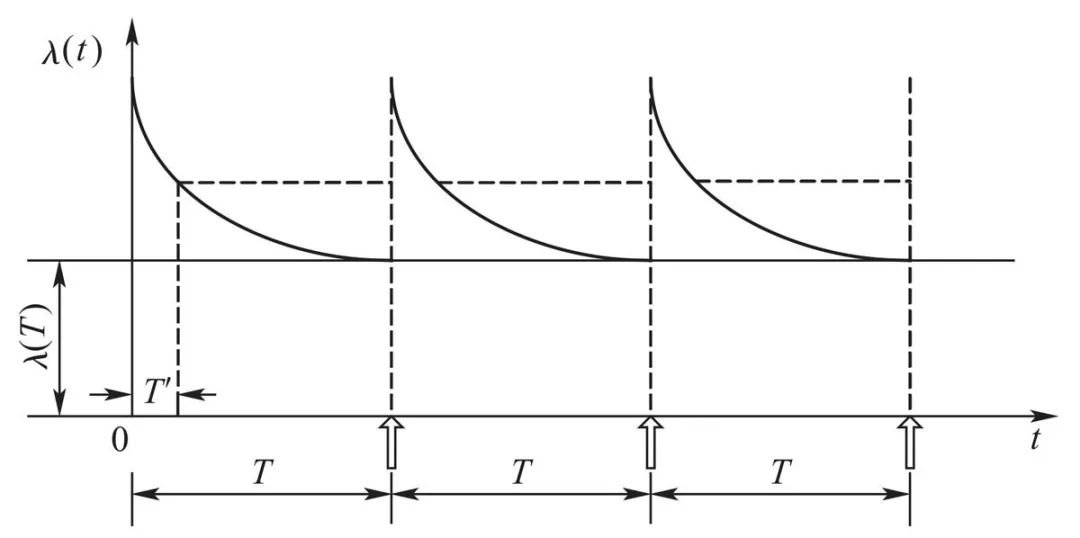
图3 定时更换产生反效果的示意图

偶然故障期，不能用定时更换的办法来预防。故障率本来是常数，即使更换了，故障率也不发生变化，定时更换无效果（见图4）。这时只能让它一直工作到有用寿命末期为止。如果更换修理，甚至会引起附加的早期故障，增加人为差错的故障。

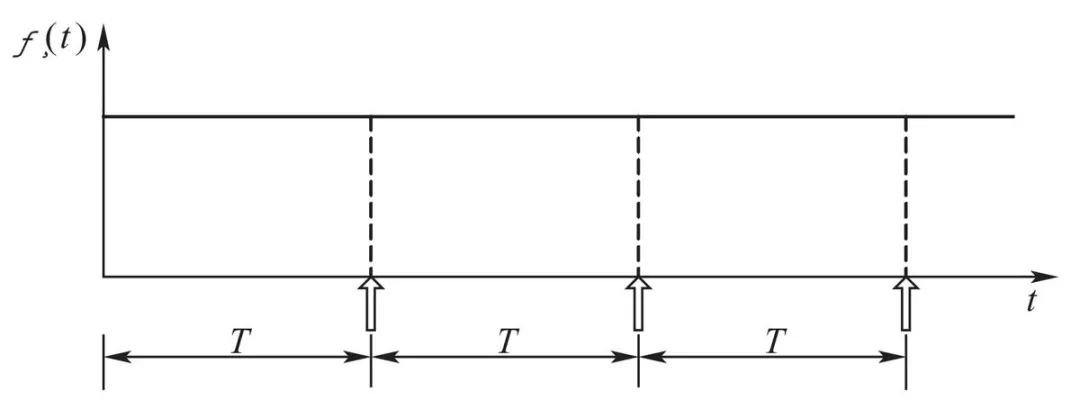
图4定时更换无效果的示意图

耗损故障期，设备的故障率开始随着时间的增加而迅速增大，表现出故障集中出现的趋势。如果在进入耗损故障期之前定时更换，故障率递增的趋势是可以控制住的。

②正态分布函数（曲线B）：其分布函数分布密度和故障率函数分别为

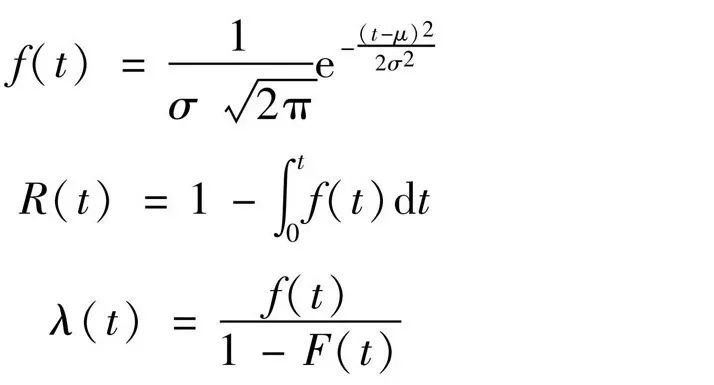
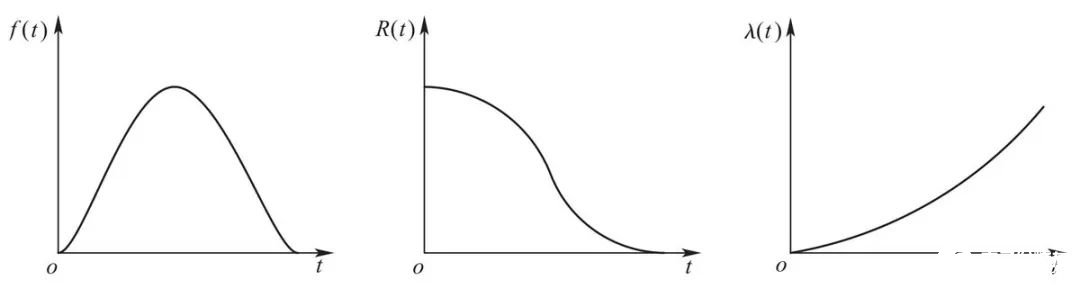
图5 正态分布曲线

正态分布曲线的维修策略：对于失效分布属于正态分布的设备，存在两种情况，分别如图6和图7所示。图6所示的设备状态变化分布范围小，故障率在短时间内快速增长，设备故障多发期的时间跨度短，故可在设备故障率急剧增长之前进行定期维修策略；图7所示的设备状态变化分布范围大，故障率增长缓慢，设备故障多发期跨越了较长的时间段，很难判断合适的维修周期，此时可采用基于状态的维修策略。

图6 定期维修



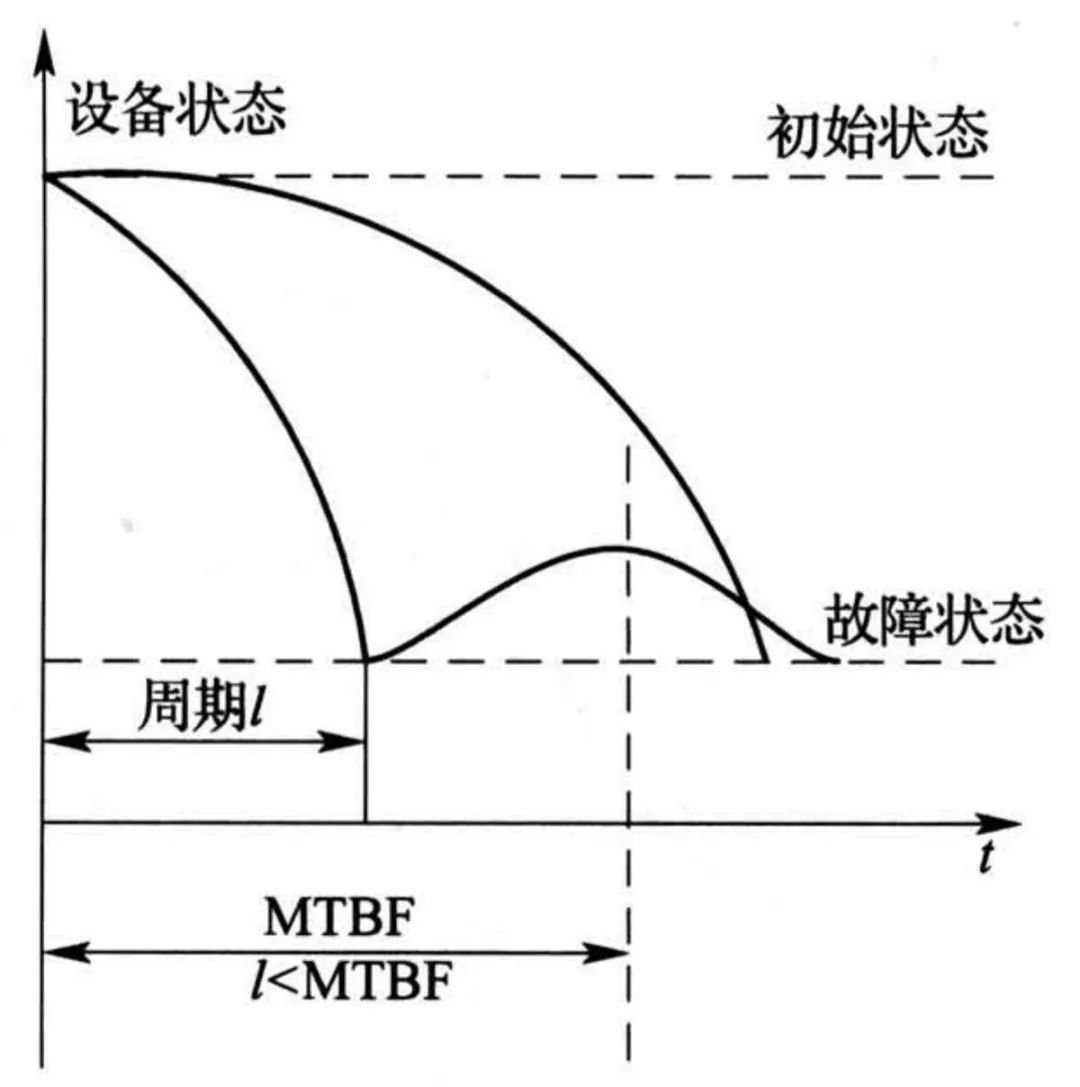
图7 基于状态的维修

③线性递增函数（曲线C）：该分布函数、分布密度及故障率函数分别为

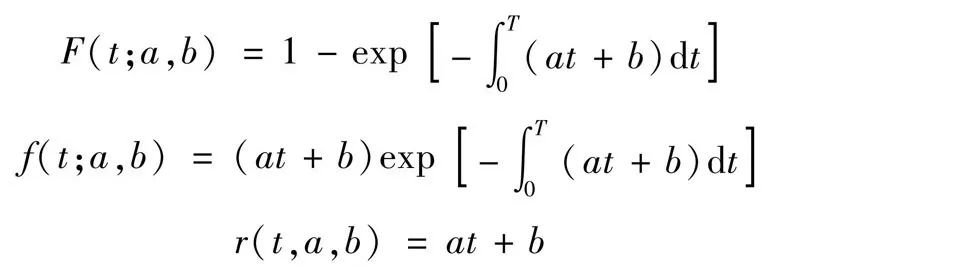
式中，a， b为系数，a代表斜率，b代表截距。

④指数分布函数（曲线E ）：其分布函数、分布密度及故障率函数分别为

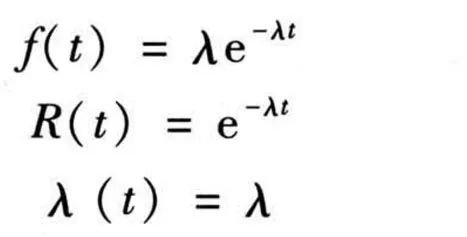
式中，1/γ为平均故障间隔时间（MTBF）。

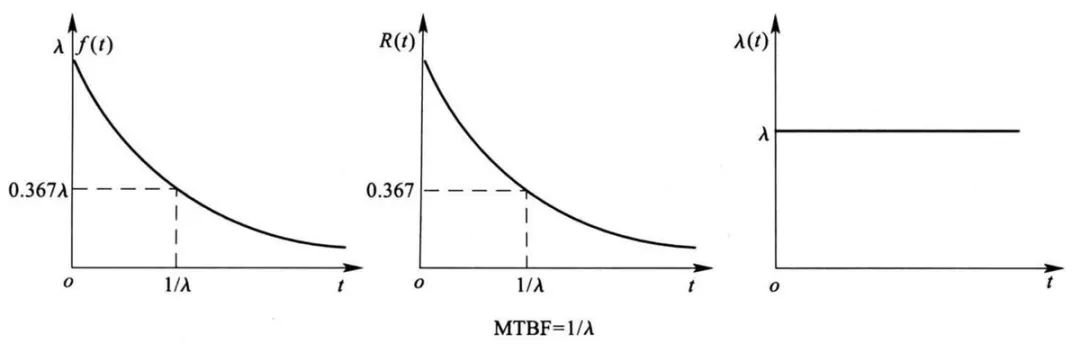
图8 指数分布相关曲线

指数分布曲线的维修策略：故障服从指数分布的设备，平均故障间隔期等于故障率γ的倒数，即1/γ。因此对于可修复系统，可以认为大约每隔1/γ时间发生一次故障，此时可以通过改进设计和检修设备来改善设备的状态。

3.复杂设备故障率曲线

复杂设备是相对简单设备而言的。简单设备是指只有一种或很少几种故障模式能引起故障的设备，复杂设备是指具有多种故障模式能引起故障的设备。

1960年12月，美国贝尔电话实验室的德雷尼克首次发表了复杂设备的故障定律，也称之为德雷尼克定律。其内容是：可修复的复杂设备，不管其故障件寿命分布类型（如指数分布、正态分布等）如何，故障件修复或更新之后，复杂设备的故障率随着时间的增大而趋于常数，如图9所示。

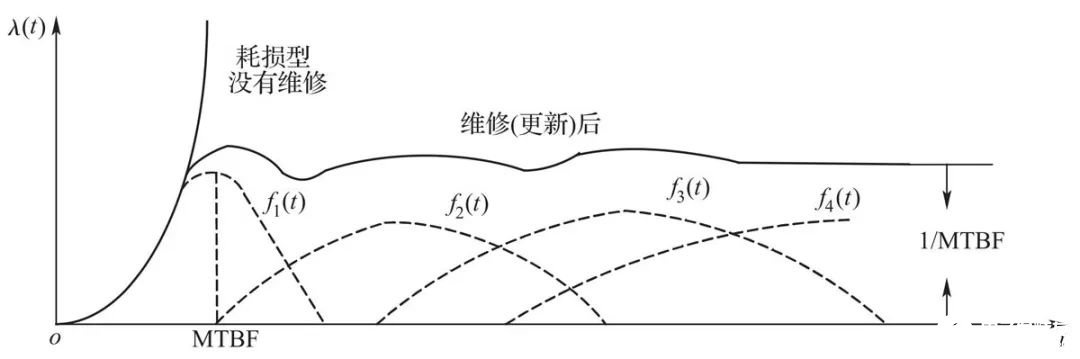
图9 复杂设备维修（更新）后的故障率曲线

复杂设备故障定律的物理解释是，复杂设备的故障是由许多不同的故障模式造成的，而每一种故障模式会在不同的时间发生，具有偶然性。如果出现了故障就及时排除— 更新的话，那么故障件的更新也具有偶然性，因而使得设备总的故障率为常数。

一般的机械设备、机电设备、电器设备和电子设备等多属于复杂设备。复杂设备的故障定律应用十分广泛，它使我们在故障机制尚不清楚的情况下，可以回避故障的物理原因，也可不必知道故障件的分布类型，为实施预防性维修工作提供了简便而又重要的理论依据。

责任编辑：gt