一个数据结构-线段树

一、概念解析

这次来介绍一个数据结构 - 线段树。

在平时刷题或是工作中，经常会遇到这么一个问题，“给定一个数组，求出数组某段区间的一些性质”。

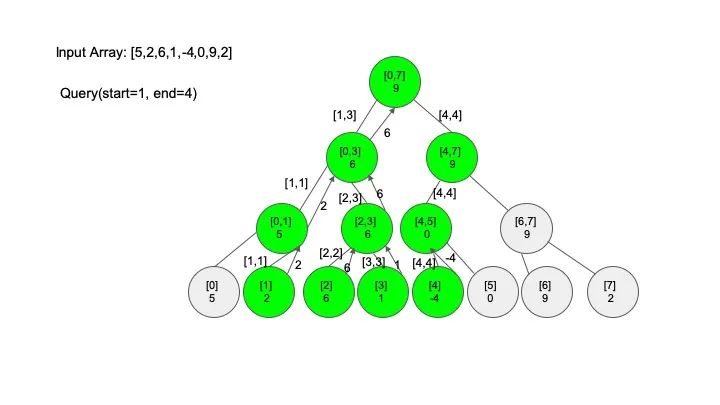
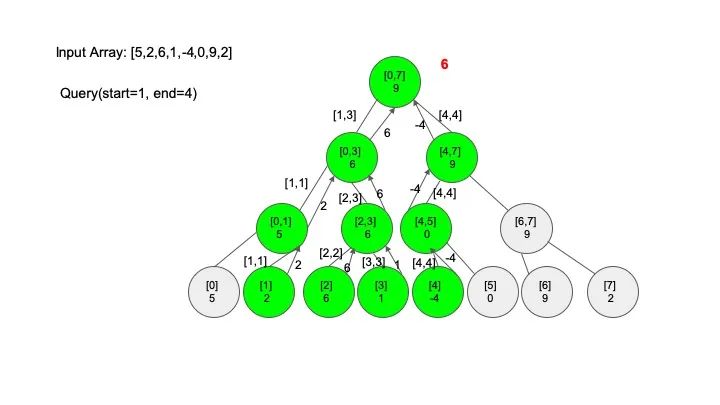
比如给定一个数组 [5,2,6,1,-4,0,9,2]，让你求出区间 [1,4] 上所有元素的和，在这个例子中，答案是 2 + 6 + 1 + (-4) = 5。

你可能会说，直接遍历一遍不就好了吗？

最简单的方式就是直接遍历一遍区间，时间复杂度也显而易见 O(n)，如果在这个数组上频繁进行这个操作，那么效率相对来说会比较低，怎么优化呢？

对于求区间和的问题，前缀和数组是一个不错的选择，构建好前缀和数组后，求一个区间和的话只要前后一减就可以了，如果不算构建数组的时间，那么每次的操作时间复杂度就是 O(1)。

这里的问题在于前缀和数组只能解决求区间和的问题，但是其他的区间问题，前缀和数组并不能很好的解决，比如求某段区间上的最大值。

因此我们需要一个数据结构能够帮助我们解决大部分数组的区间问题，而且时间复杂度要尽可能的低。

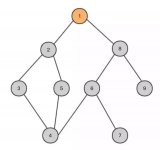
这也就是今天的主题 - 线段树，首先要说明一点的是，线段树也是二叉树，只是它的节点里面含有区间的信息。

线段树每个节点表示的是一个区间，每个节点将其表示的区间一分为二，左边分到左子树，右边分到右子树，根节点表示的是整个区间（也就是整个数组），叶子节点表示的是一个 index（也就是单个元素），因为每次对半分的缘故，线段树构建出来是平衡的，也就是说树的高度是 O(logn)，这里的 n 表示的是数组中所有的元素，这一点对于我们后面分析复杂度很重要。

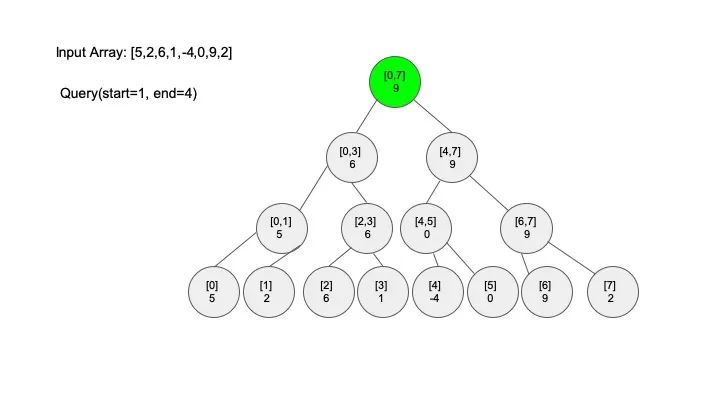
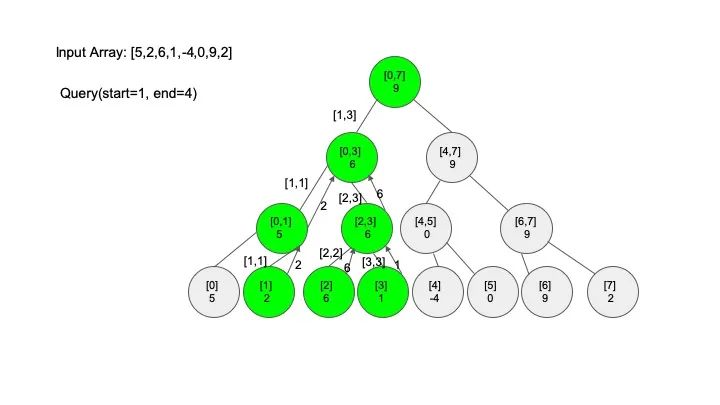
线段树有三个基本的操作，分别是构建线段树(build)、区间查找(query)、还有就是修改(modify)，假设我们现在需要解决的问题是 “求区间上的最大值”，例子还是之前的例子，一起来看看怎么实现这些操作。

对于构建操作来说，相对简单，你只需要记住 “自上而下而下递归分裂，自下而上回溯更新” 从根节点到叶子节点我们不断地将区间一分为二，从叶子节点开始返回值，一直到根节点，不断地更新区间信息。

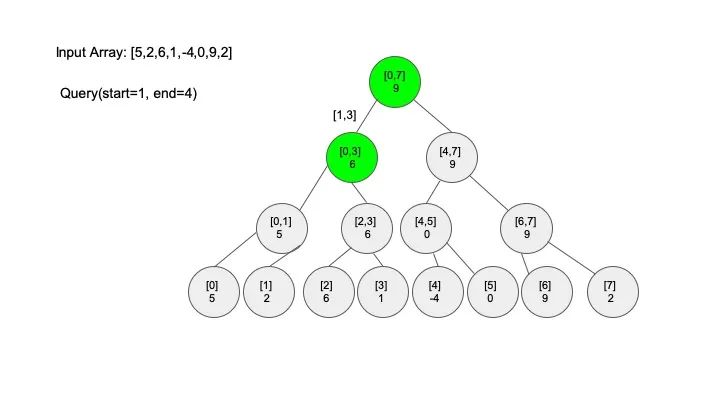
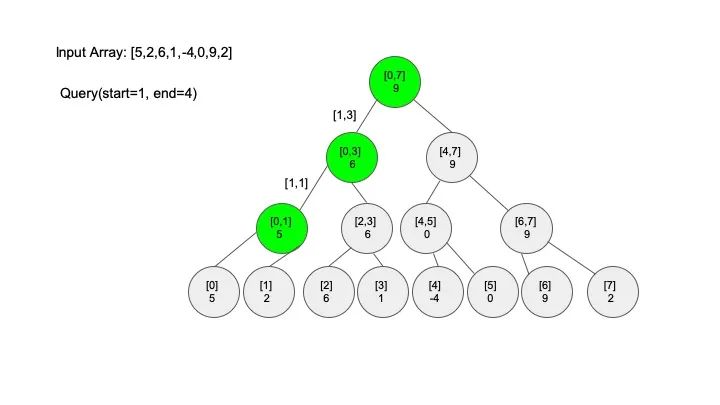
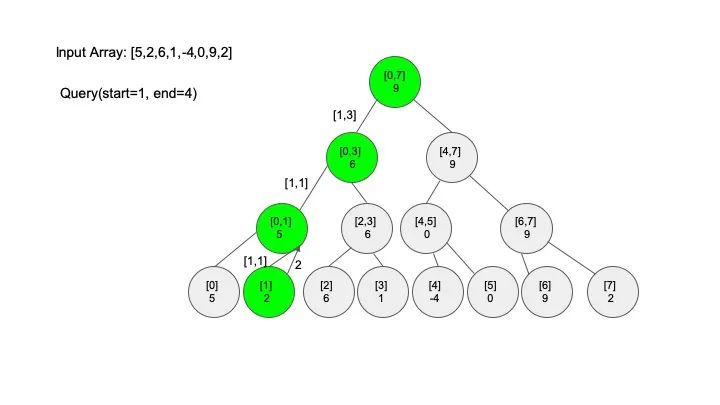
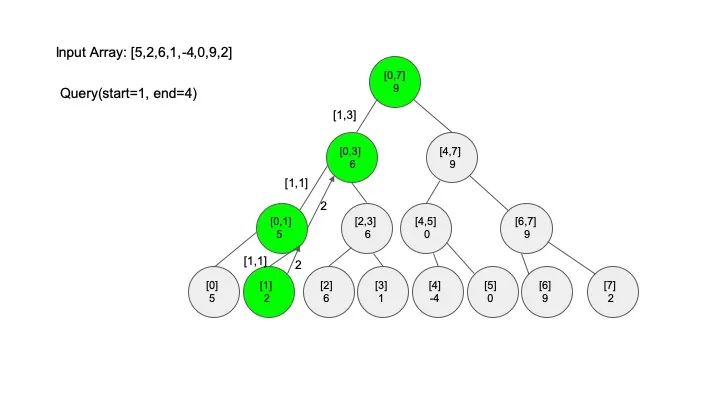
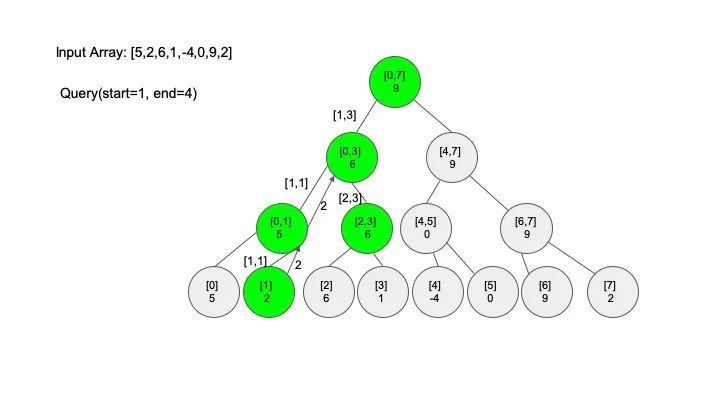
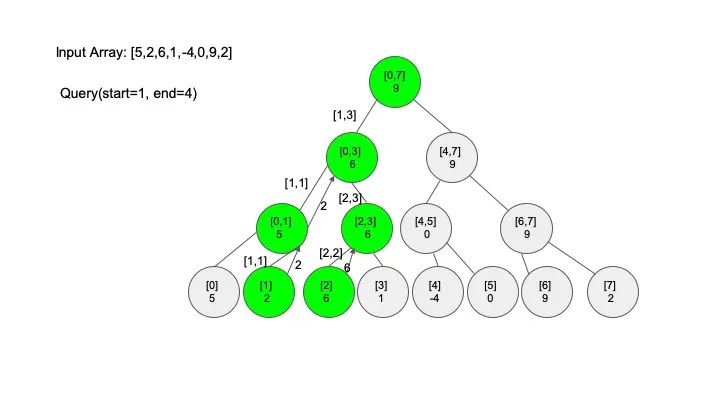
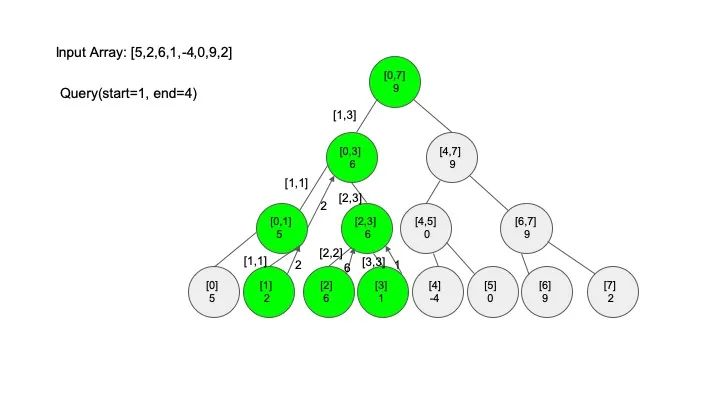
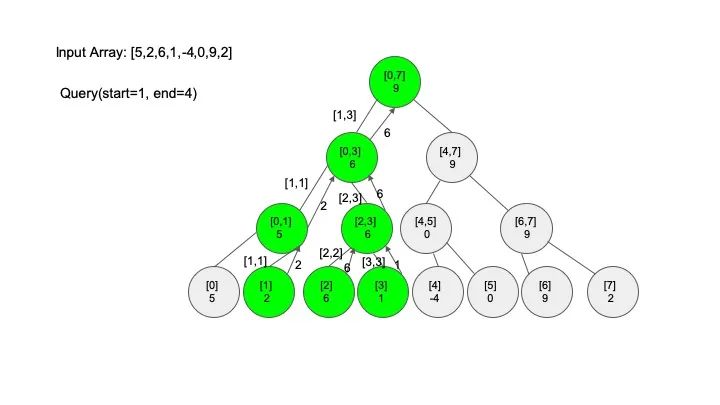
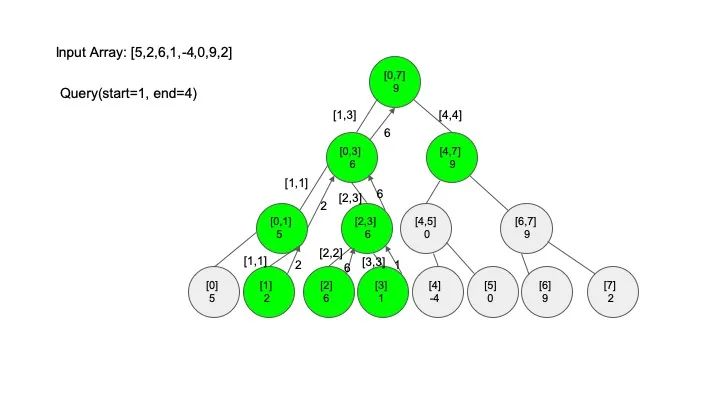
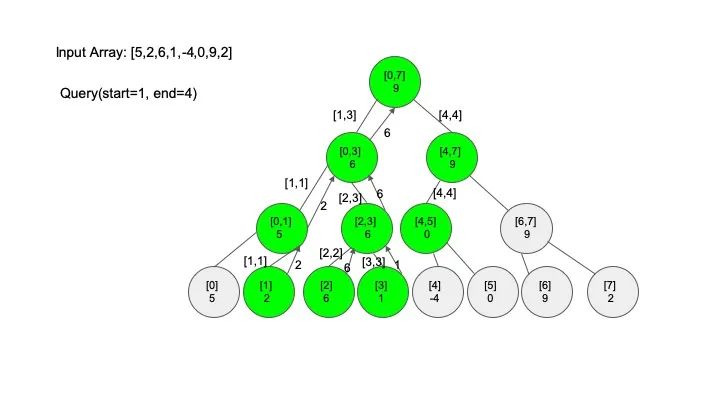
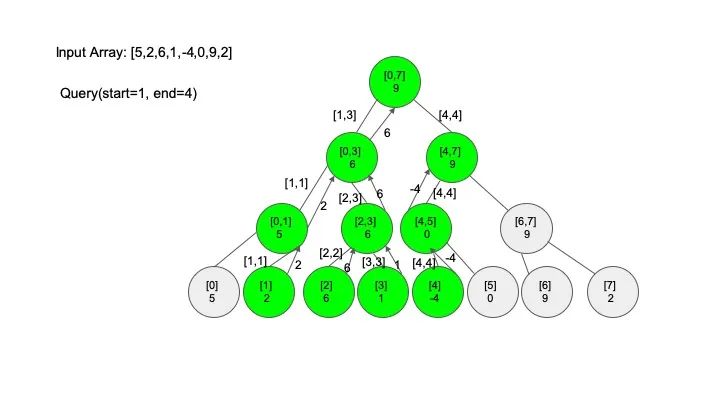
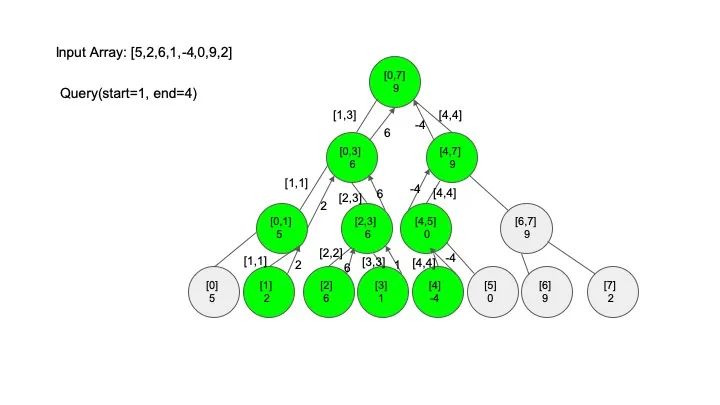
查找操作是线段树的核心操作，考虑的情况相对较多，这里有四种情况：

情况一：节点区间包含查找区间。这种情况直接递归向下查找即可

情况二：节点区间不相交于查找区间。因为没有要查找的范围，停止搜索

情况三：节点区间相交但不包含查找区间。将区间分成两段，分别查找

情况四：节点区间相等于查找区间。直接返回答案

说明一下，这里说的 “包含” 的意思是一个区间全部元素都被另外一个区间涵盖，“相交” 的意思是一个区间的部分元素被另外一个区间涵盖，例如要查找的区间是 [1,3]，那么 [0,4] 包含要查找的区间，[2,5] 只是相交要查找的区间。对于区间查找，后面有图解，跟着例子走一遍印象会更深刻。

最后一个修改操作，和构建操作类似，但有些许不同，你只需要记住 “自上而下递归查找，自下而上回溯更新”。修改的意思是，修改数组中的一个元素的值，这会影响相关的区间，相关的树节点，因此，相关联的节点也就需要更新。

线段树灵活的地方在于，树节点中存放的数据不同，它的功能就不同，比如说，你想要求解区间和，那么树节点中就存放对应区间元素的和，你想求解区间上的最大值，那么树节点中存放的就是对应区间上的最大值。不过话说回来，线段树并不是一个被广泛应用的数据结构，原因可能在于线段树的构建和使用相对于前缀和数组这样的技巧来说，稍微复杂了些。但是在解决数组区间的问题上，线段树可以提供一个还不错的思考方向。

二、动画描述

三、代码实现

publicclassSolution{ privateclassSegmentTreeNode{ intstart,end,max; SegmentTreeNodeleft,right; SegmentTreeNode(intstart,intend,intmax){ this.start=start; this.end=end; this.max=max; this.left=this.right=null; } } publicSegmentTreeNodebuild(intstart,intend,int[]nums){ if(start>end){ returnnull; } if(start==end){ returnnewSegmentTreeNode(start,end,nums[start]); } SegmentTreeNodenode=newSegmentTreeNode(start,end,nums[start]); //自上而下而下递归分裂 if(start!=end){ intmid=(start+end)/2; node.left=build(start,mid,nums); node.right=build(mid+1,end,nums); } //自下而上回溯更新 if(node.left!=null&&node.left.max>node.max){ node.max=node.left.max; } if(node.right!=null&&node.right.max>node.max){ node.max=node.right.max; } returnnode.max; } publicintquery(SegmentTreeNoderoot,intstart,intend){ //如果节点区间相等于查找区间，直接返回对应的值即可 if(root.start==start&&root.end==end){ returnroot.max; } intmid=(root.start+root.end)/2; intleftMax=Integer.MIN_VALUE,rightMax=Integer.MIN_VALUE; //判断是否需要去左子树查找 if(start<= mid) {             // 节点相交查找区间的情况             if (end >mid){ leftMax=query(root.left,start,mid); }//节点包含查找区间的情况 else{ leftMax=query(root.left,start,end); } } //判断是否需要去右子树查找 if(mid< end) {             // 节点相交查找区间的情况             if (start <= mid) {                 rightMax = query(root.right, mid + 1, end);             } // 节点包含查找区间的情况             else {                 rightMax = query(root.right, start, end);             }         }         return Math.max(leftMax, rightMax);     }     public void modify(SegmentTreeNode root, int index, int value) {         // 找到对应的叶子节点，进行元素更新         if (index == root.start && index == root.end) {             root.max = value;         }         if (root.start >=root.end){ return; } //自上而下递归查找 modify(root.left,index,value); modify(root.right,index,value); //自下而上回溯更新 root.max=Math.max(root.left.max,root.right.max); } }

四、复杂度分析

三个操作中，构建树的操作的时间复杂度是 O(n)，原因也很好解释，构建的树有 2n 个节点，你可能会问这个 2n 是怎么得到的，思考这个问题可以从叶子节点出发，一共有 n 个叶子节点，构建操作是从上往下不断二分，这样保证了树的平衡，因此所有节点个数就是 n + n/2 + n/4 + ... + 1 = 2n。

由于构建每个节点只花了 O(1) 的时间，因此整个构建的时间复杂度就是 O(2n)，忽略常数项，也就是 O(n)。

修改和查找都是沿着一条或者几条从上到下的路径进行的，因为树的高度是 O(logn)，所以这两个操作的时间复杂度也是 O(logn)。可以看到这个时间复杂度比暴力的 O(n) 还是快不少。