考量运算放大器在Type-2补偿器中的动态响应（第一篇）

考量运算放大器在Type-2补偿器中的动态响应（第一篇）

补偿器是使控制系统在动态运行中快速稳定的电子滤波器。在绝大多数研究中，补偿器是置于运算放大器(运放)周围的一个有源电路，其特性鉴定为完美。如果这种方法适用于低带宽系统，如今的转换器即使输出电容小，只要交越频率超过100千赫就能确保足够快的瞬态响应以限制输出压降。 在这些应用中，若一个完美运放不行的话，最终会导致严重的增益和相位失真。如果展示开环增益和所选运放的低、高频两个极点如何影响整体动态响应，您就可选择恰当的元件，免除影响交越所需的增益和相位性能表征。文本共有两部分，这第一部分主要介绍开环增益的影响，特意先不谈低频和高频两极点。

01

不同补偿器的类别

补偿器的作用是形成一个给定电路的频率响应，以便一旦闭环，控制系统表现出所需的交越频率fc和适当的相位/增益裕度。补偿器通过在fc的一些中期波段的增益或衰减强行形成0 dB交越点。相位裕度jm由补偿器在fc表现出的相位提升(phase boost)量调节。增益裕度取决于交越后补偿器调降增益的能力。 补偿器有不同的类型，其在开关转换器中通常称为type 1、type 2和type 3。所有三个型号在原点都有一个极点以提供最大可用准静态增益（S=0），从而提供一个精确的输出变量。type-1补偿器是个简单的积分电路，完全不提供相位提升。type 2基于type 1，增加了一个极/零对，最多有90°的相位提升，常见于电流模式电源，可提供大量补偿。type-3电路提供另一个极零对，可提升相位达180°。更多信息请查阅[1]。

图1：您选择的补偿器与您想要的相位提升量有关

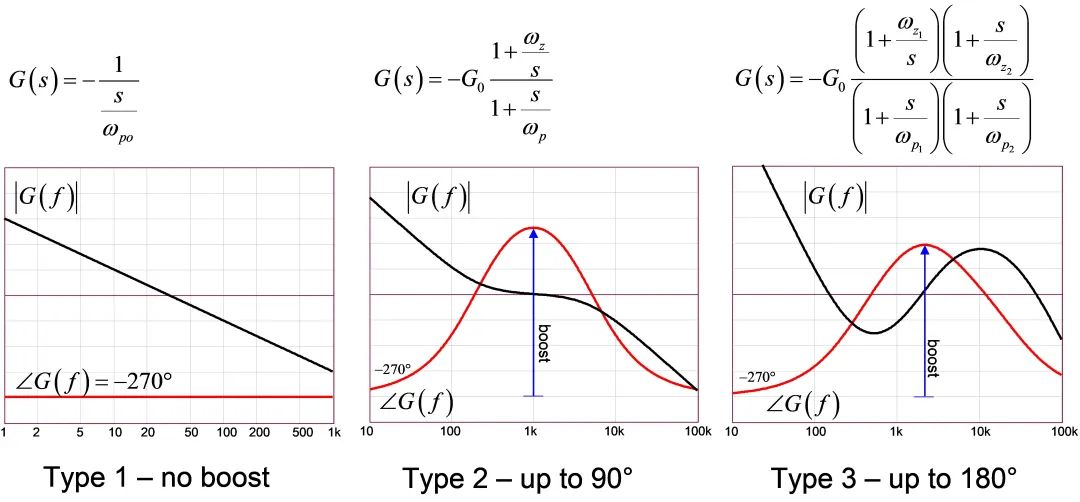
Type 1 – 无提升

Type 2 – 提升达90°

Type 3 – 提升达180°

02

简介快速分析技术（FACTs）

快速分析技术（Fast Analytical Techniques ，简称FACT）的基本原理是确定在两个不同条件下的电路时间常数：激励信号消失（Vout降至0V）时和响应清零（VFB=0）时。 一个具有非零准静态增益的第一阶系统的传递函数可表示为：

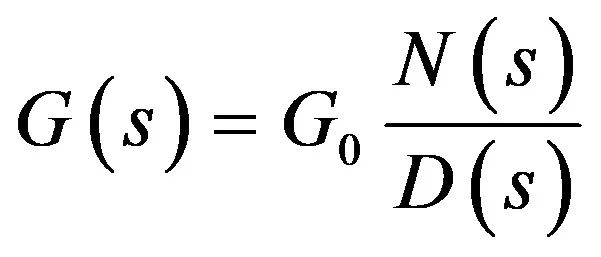
（1）

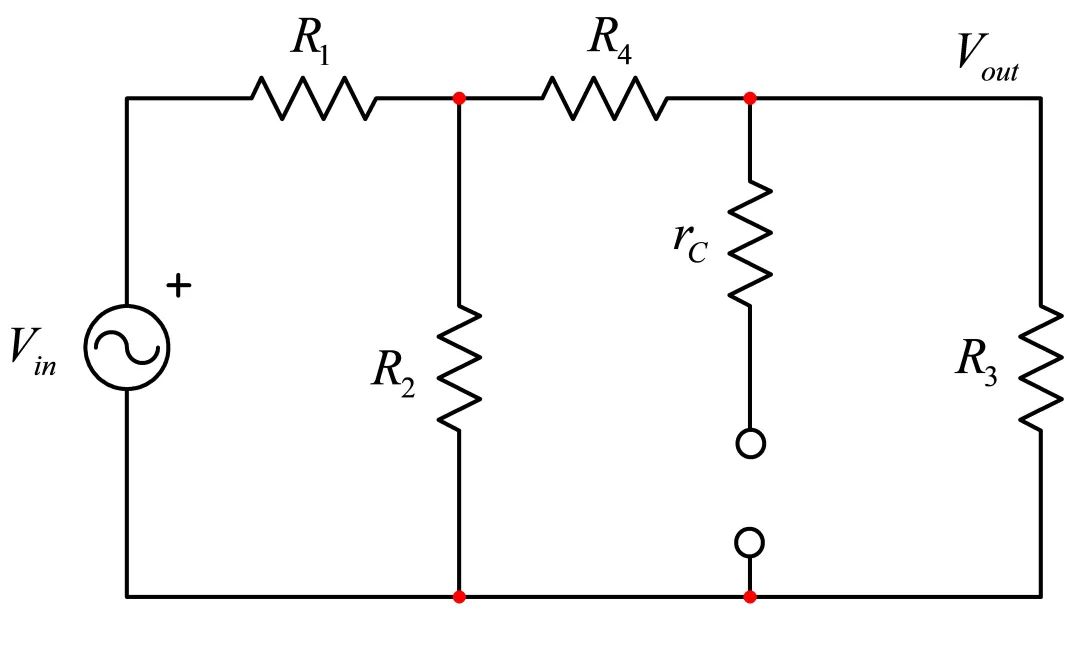
首项G0是S=0时系统表现出的增益。分子的N(s)控制传递函数的零点。在数学上，零点是个特定的点sz，无信号响应。从理论上讲，考虑到激励信号覆盖整个s面（谐波模式下不仅在垂直轴），当输入信号调到零角频率sz，零点表现为无信号的输出响应。电路中一些特定阻抗组合阻挡了信号传播，响应为0V，尽管存在激励源。零点是分子的根。 分母D(s)由电路自然时间常数构成。通过设置激励信号为0和确定这种结构中所考虑的电容或电感“所示”的阻抗而得出这些时间常数t= RC或t= L/R。如您想象把欧姆表置于暂时移除的电容或电感器，并读取它显示的电阻。您看图2的无源电路，可看到一个注入源（换言之，一个激励源）正加偏压于左边网络。输入信号通过网格和节点传输，形成您看到的电阻R3上的响应。

图2：确定电路的时间常数需要将激励源设为0，并看看从电路中暂时移除的能量存储元件所提供的电阻。

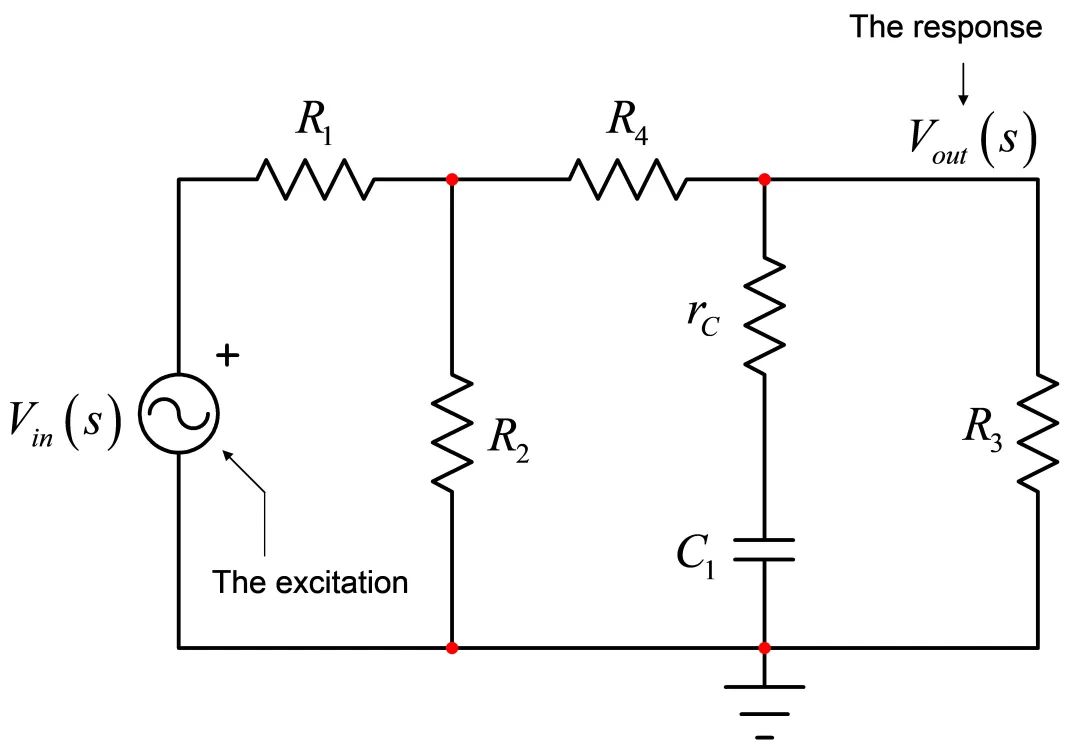
The response：响应

The excitation：激励源

本例我们将激励源设为0（由短路代替0V电压源，开路代替0A电流源），拆下电容器。然后我们想象连接一个欧姆表，以确定由电容器端提供的电阻(如图3)。

图3：由短路代替0V源后确定电容器端的电阻。

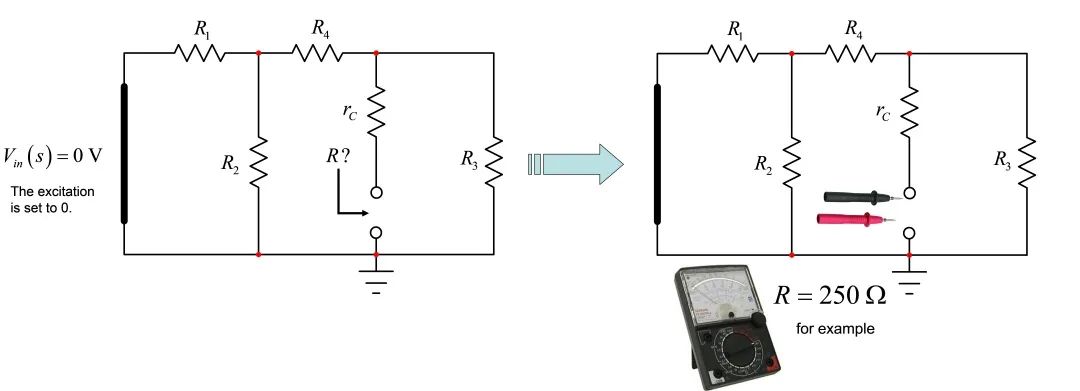
The excitation is set to 0：激励源设为0

For example：例如

您“想象” R1与R2并联后与R4串联，所有这些与R3并联后与rC串联。该电路的时间常数只通过R和C1即可计算得出：

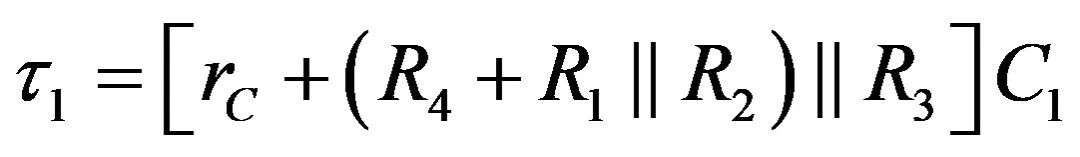
（2）

我们可证明，第一阶系统的极点是其时间常数的倒数。因此：

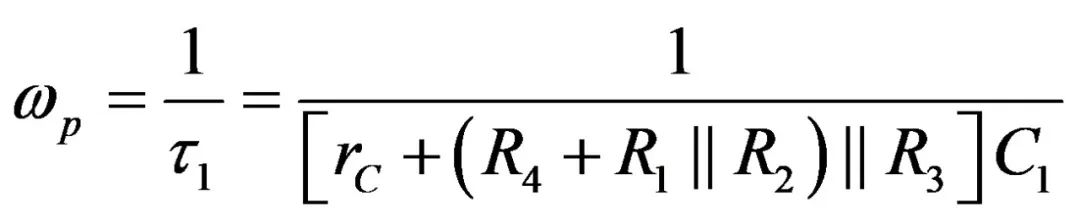
（3）

s = 0时这个电路的准静态增益是多少？在直流条件下，电感器短路，电容器开路。把这概念应用于图2的电路，绘制成如图4所示。想象在R4前断开连接，会看到一个含R1和R2的电阻分压器。R2上的戴维宁(Thévenin)电压为：

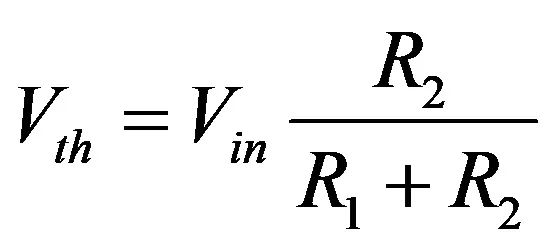
（4）

输出电阻Rth是R1与R2并联的值。因此完整的传递函数涉及到电阻分压器(由与Rth串联的R4和加载的R3所构成)。rC是断开的，由于电容C1在这直流分析中被移除。因此：

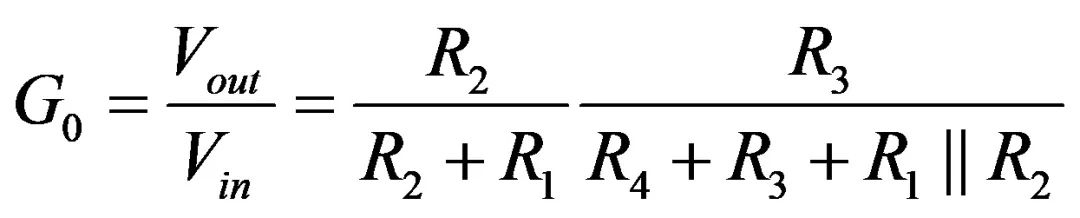
（5）

图4：您断开直流电路中的电容器，计算这简单的电阻配置的传递函数。

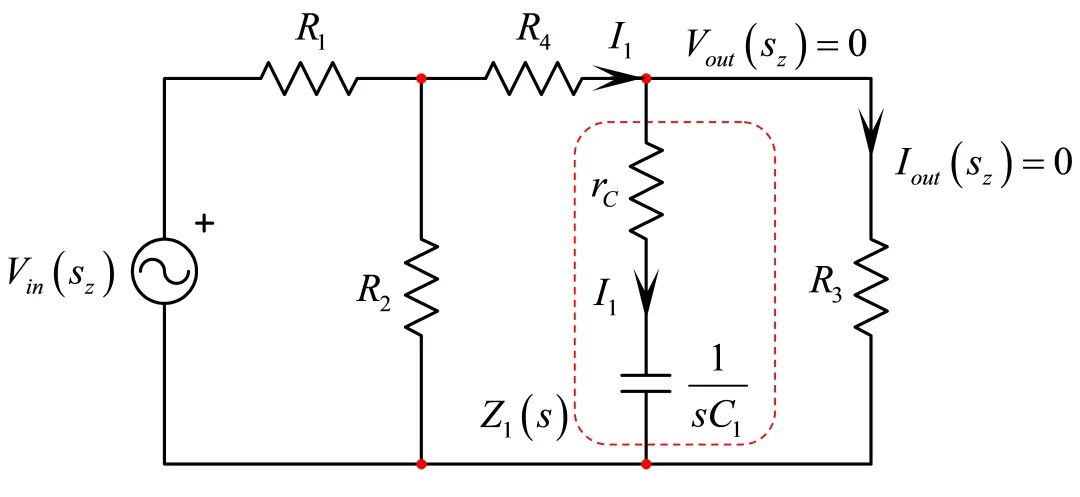
我们如何知道是否有零点？技巧是：您想象图2的电路，使电容C1短路。现在假设您为具有短路电容器的电路提供激励信号。您能够基于示波器观察Vout的响应吗？当然rC使R3短路，尽管振幅可能低，输入信号仍会传输并有响应。若“尽管C1短路但仍有响应”，那么有与C1有关的零点。处理含电感L1的电路亦然(但采用电感开路)。 零点通过阻断激励信号的传输而在电路中表现出来，输出响应为0。若我们考虑一个变形电路–其中C1由代替–如图5，当激励源加偏压于电路，有什么特定的条件意味着无信号响应？无信号响应只意味流过R3的电流为0。若电阻没有电流，没有电压施加和Vout是0 V，这不是短路，而是虚拟的接地。

图5：在这变形电路中，当串联的rC和C1转化为短路，响应消失。

若R3没有电流，那么串联的rC和转化为短路：

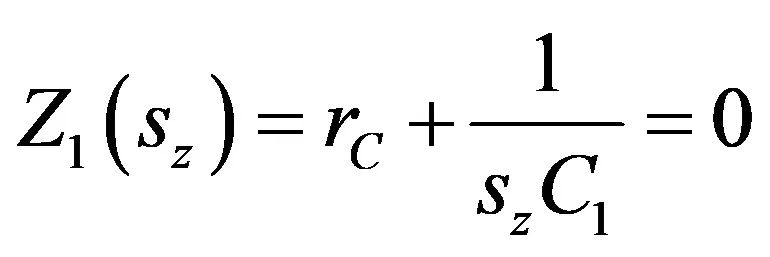
（6）

根sz是我们想要的零点位置：

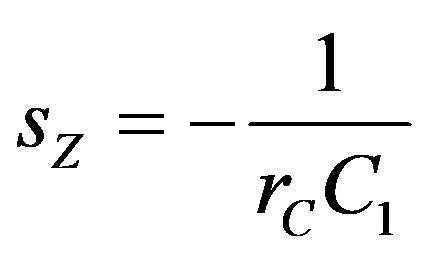
（7）

从而有：

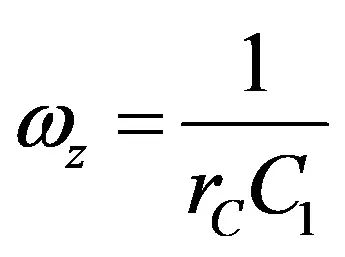
（8）

现在，我们可组合所有这些结果，形成以图2电路为特征的最终的传递函数：

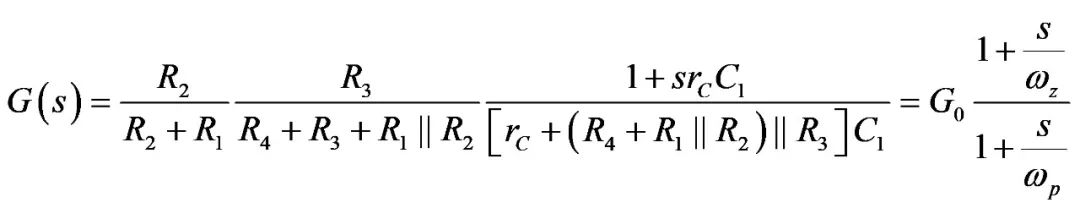
（9）

这就是所谓的低熵表达式，您可立即识别增益、极点和零点。高熵表达式将在考虑阻抗分压器时通过施加大规模外力到原来的电路来获得，如：

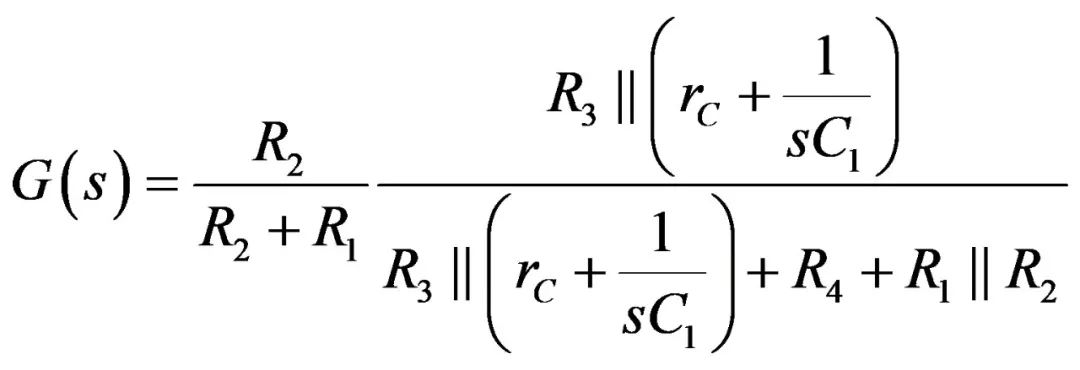
（10）

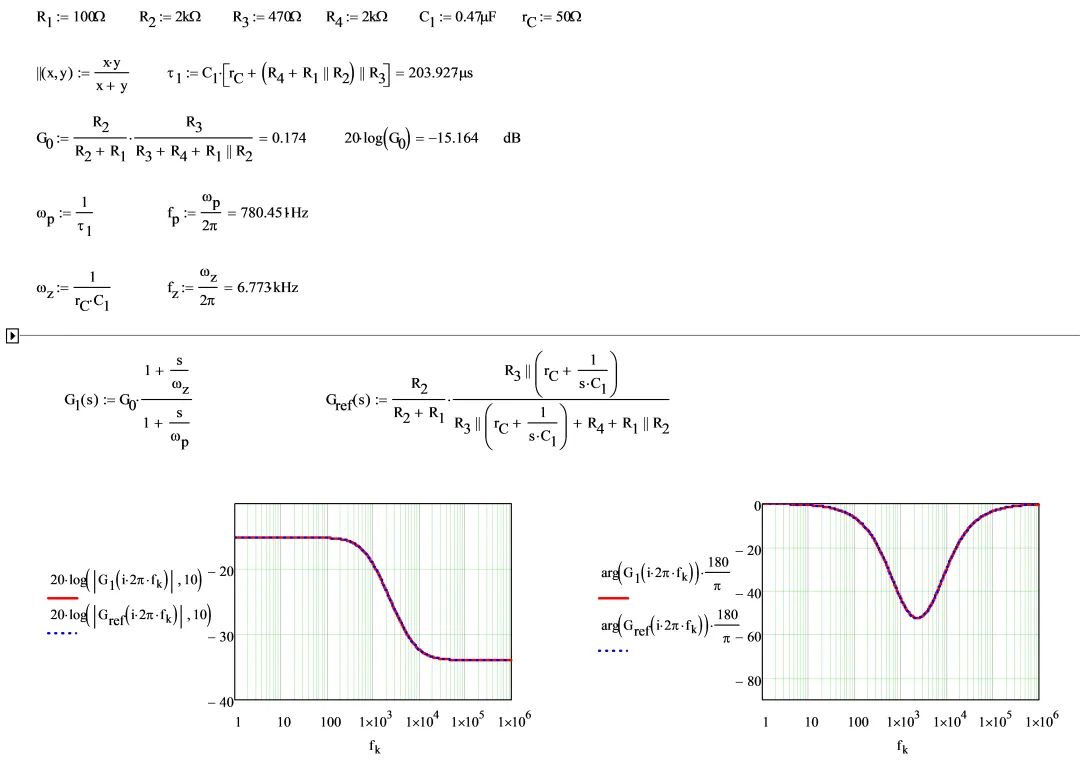
请注意（9）没有一行代数。这易于发现错误时单独修复。（9）的校正很容易。现尝试对（10）进行相同的修正，无需从头开始。您比对一下，采用Mathcad表绘制的表达式（9）和（10）的频率响应相同（图6）。

图6：快速Mathcad显示用FACT推导出的表达式是否与由原表达式返回的响应相匹配。