本文讲解FIR滤波器的第二种设计方法——频率取样法。
我们在上一篇的末尾也曾总结过,窗函数法是从时域出发的一种设计方法,不直观。为什么呢?因为我们设计滤波器更关注的是它的频率特性(至少在现阶段是如此),可不可以直接从它的频率性能出发来设计滤波器呢?当然可以,这就是本篇我们要说的“频率取样法”。
三频率取样法
1. 设计原理
顾名思义,频率取样法,就是在频域上取样,取谁的样?当然是取滤波器的频率响应,也就是说:
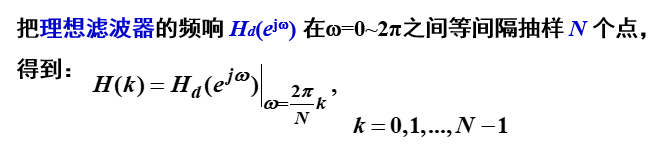
得到的这N个离散样本值之后,下面怎么办?
我们知道,本章我们设计滤波器的终极目标(现阶段哈,理论上的终极目标)就是得到描述滤波器的系统函数H(z)分子和分母多项式的系数。而对于FIR滤波器,分母为1,分子系数就是其单位冲激响应h(n)。所以,下一步,就是求出h(n)。
得出了H(k),怎么得到h(n)呢?该我们学过的法宝DFT隆重登场了,只不过这次是逆变换:IDFT。

好啦,现阶段终极目标实现了。看上去似乎很简单,但是......拿这个h(n)当我们的终极目标,靠谱吗?
所以我们需要分析一下,这个h(n)代表的滤波器的滤波特性到底如何?能不能达到设计指标要求?
通过前面学习窗函数法,我们知道,窗函数法得到的h(n)是对理想滤波器的hd(n)进行截断得到的,所以滤波性能比理想滤波器差。那么,我们通过前面的过程得到的h(n),它与理想滤波器的hd(n),又是什么关系呢?或者说,h(n)代表的实际FIR系统的频率响应H(e^jw),与hd(n)代表的理想滤波器频率响应Hd(e^jw),是什么关系呢?下面用两种方法进行分析:
2. 逼近误差
第一种分析方法:分析h(n)与hd(n)的关系
我们的“时频域终极对应关系”——一个域离散抽样,另外一个域周期延拓,又要登场了。看下图:
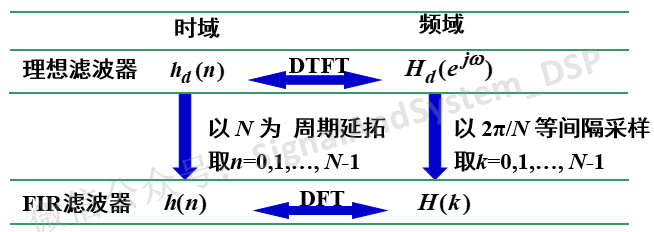
图1
频域上,将Hd(e^jw)以2Π/N为间隔离散抽样,对应到时域上,就是将hd(n)以N为周期延拓。而DFT是时域频域都取主值区间,所以用公式来描述这句话,就是:
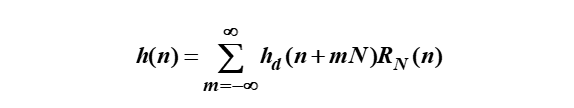
看到这里,我们就要想到了,hd(n)是无限长的,把它周期延拓肯定会混叠啊,再取主值区间得到的h(n),其数值肯定与hd(n)不同了。也正是因为这个”混叠“,才导致我们得到的FIR的频率响应H(e^jw),肯定不如理想滤波器的Hd(e^jw)。
第二种分析方法:分析H(e^jw)与Hd(e^jw)的关系
继续前面一句话,H(e^jw)不如Hd(e^jw),到底哪里不如呢?H(e^jw)表示不服气“说我不好,给出证据来!”
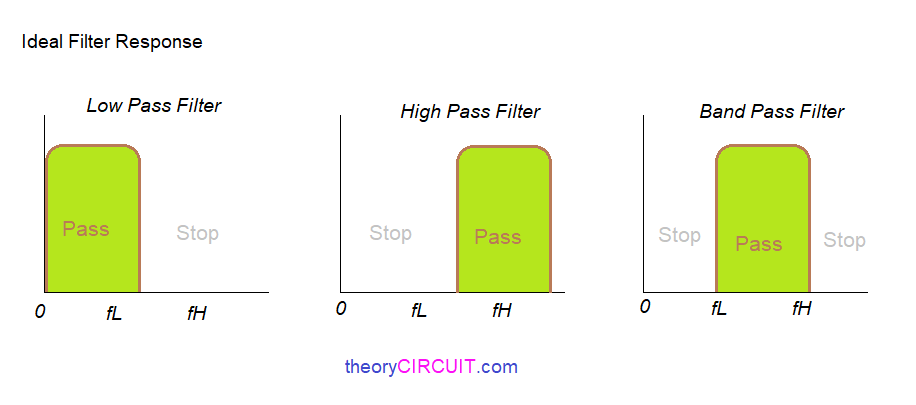
我们知道,Hd(e^jw)是理想滤波器的频响,它的模样我们很清楚,表达式我们也能写出来,以低通为例,就是下面的样子:
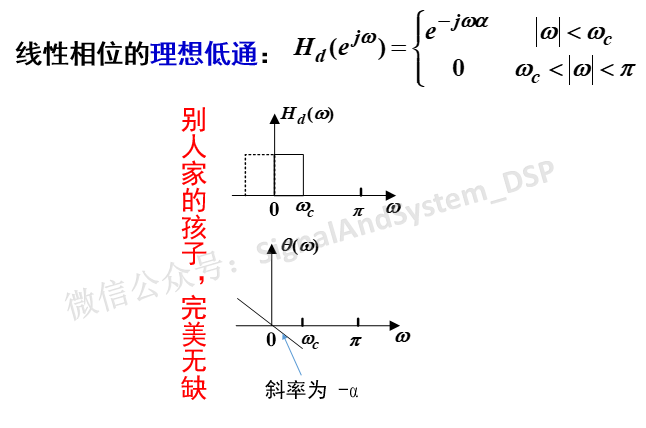
图2
我们自家的孩子H(e^jw),是什么样子呢?表达式能不能求出来呢?
我们回到图1:H(e^jw)是h(n)的傅里叶变换(DTFT),而h(n)的DFT是H(k),根据前面所学,DFT就是DTFT一个周期([0~2Π])的N个等间隔抽样值。根据频域抽样中所学的“频域的插值恢复”,有下面的公式来表示H(e^jw):

图3
抱歉,我知道这个公式很烦人,可是不把它摆出来,不能让自家的孩子H(e^jw)心服口服啊。
说了这么多,理顺一下:频率取样法的思路是:把完美无缺的别人家的孩子Hd(e^jw),离散抽样出N个点,得到H(k),然后把H(k)求N点IDFT,得到h(n),这就是我们自家的孩子,它的频率响应H(e^jw)是什么呢?就是我们图3中的内插公式来表示。
下面用图形直观说明自家的孩子与别人家孩子的差距,以低通滤波器为例。
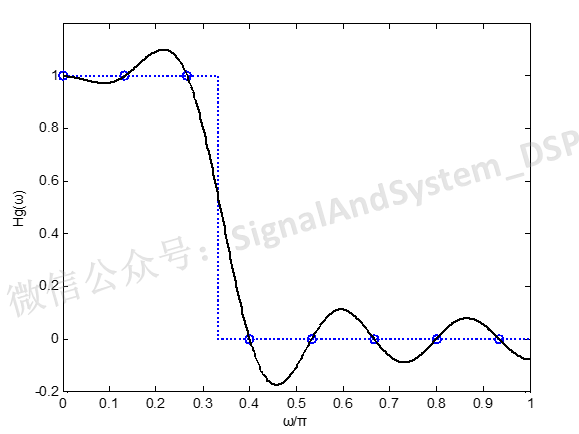
图4
图4中,蓝色虚线是“别人家的孩子”——理想低通滤波器的幅频特性,截止频率为π/3,按照频率取样法(点数N=15,如图中蓝色空心圆点所示,因为图中只给出了0~π范围内的图,所以只显示7个点)。
需要强调说明的是,H(k)是理想低通的频谱取样值(包括幅度和相位),而我们画图时,为了简便,只给出幅度函数。
按照这些离散的频率样值点内插得到的实际滤波器(也就是自家的孩子)的幅频特性是什么样的呢?是图4中的黑色实线。
哇,不比不知道,一比吓一跳。自家孩子的差距一目了然。第一个缺点:通带和阻带之间出现了过渡带;第二个缺点:通带和阻带内出现了起伏。
这两个缺点能不能克服呢?
首先看第一个缺点,能不能尽量减小过渡带呢?显然是可以的,过渡带宽度≈两个相邻采样点的距离,即2π/N。那么,增大N,过渡带就可以变窄。
我们把N从15增大到75点(如图中红色实心小圆点,0-π之间是38个),再利用这75个频率取样值内插得到的FIR滤波器的频率响应,如图5中的红色实线,果然,过渡带变窄了。
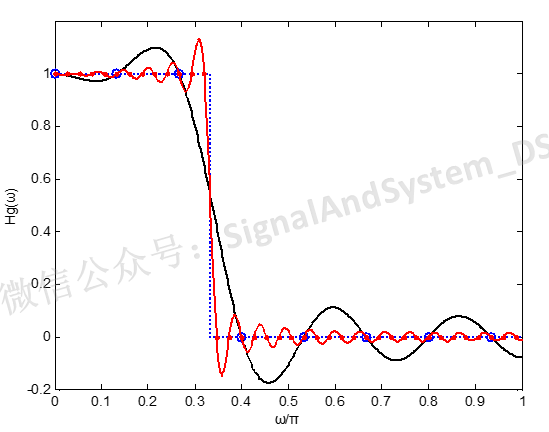
图5
但是,我们比较图5中的红色实线与黑色实线,就会发现,虽然远离截止频率的通带和阻带内部,红色实线的起伏小于黑色实线,但是第一旁瓣的起伏并不能显著改变,也就是说,增大N不能减小阻带最小衰减。
老母亲在刚刚要长舒一口气时,又绝望地发现,自家孩子的第二个缺点是基因造成的,无法改变。
不要绝望,虽然无法彻底根除,但能不能稍加改善呢?这就是我们的第三个问题:改进措施。
3.改进措施
要想改进,先找原因。产生起伏的原因,是因为样本值H(k)突然从1变为0(间断点),如果我们让它变得慢一点,就有望减小起伏。也就是说:
在频率响应间断点附近区间插入一个或几个过渡采样点,使不连续点变成缓慢过渡带。图5所示为插入一个过渡采样点的示例。
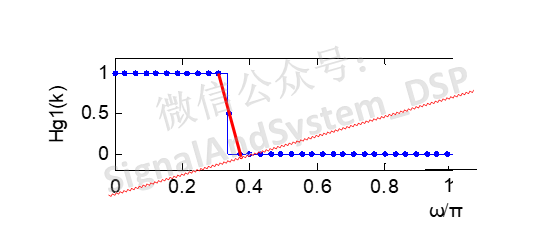
图5
插入m个过渡点,过渡带宽度近似为:(m+1)×2Π/N
过渡点个数m与滤波器阻带最小衰减之间的关系有一些经验数据,如下表所示。

而且,过渡采样点的数值需要进行优化设计,不同的取值,会影响阻带衰减。
看来,改造自家孩子,向着别人家孩子逼近,是一项光荣而艰巨的、近乎不可完成的任务啊。
老母亲们该怎么办呢?第一,选定方法,用什么方法来设计你自家的孩子,窗函数法、还是频率取样法,抑或是我们这里没讲到的最优化的方法......;第二,既然选定这种方法,说明它肯定有吸引你的优点,但是同时,你只能坦然接受这种方法命中注定的缺点。如果你发现这个缺点你无法接受,那对不起,你只好推翻重来,重新用其他方法来设计你的滤波器。
当然了,滤波器可以重新设计,但孩子只能养一次,就好比发射卫星,一旦发射失败了,只好重新造一颗了。
-
滤波器
+关注
关注
161文章
7884浏览量
179147 -
函数
+关注
关注
3文章
4350浏览量
63051
原文标题:数字信号处理系列串讲第19篇(数字滤波器之二)——FIR滤波器(3):频率取样法(1)
文章出处:【微信号:SignalAndSystem_DSP,微信公众号:信号与系统和数字信号处理】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
模拟低通滤波器的设计方法有哪些
基于FPGA实现FIR数字滤波器
滤波器Q值与截止频率的关系
FIR滤波器的工作原理和特点
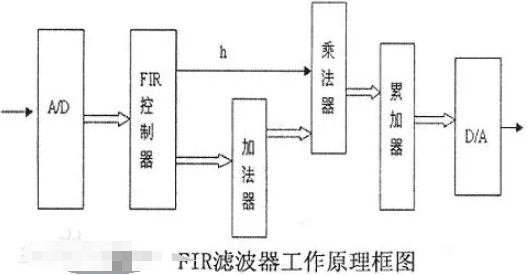
如何区分IIR滤波器和FIR滤波器
iir滤波器和fir滤波器的优势和特点
高通滤波器和低通滤波器判别方法
基于matlab FPGA verilog的FIR滤波器设计
DSP教学实验箱_DSP算法实验_嵌入式教程:4-3 有限冲激响应滤波器(FIR)算法(CCS显示)
Matlab生成fir滤波器抽头系数
Vivado 使用Simulink设计FIR滤波器
Vivado经典案例:使用Simulink设计FIR滤波器




 FIR滤波器的第二种设计方法——频率取样法
FIR滤波器的第二种设计方法——频率取样法











评论