数字滤波和分形理论的分析和原理

1、 数字滤波分析

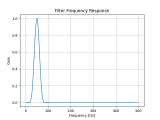
根据数字滤波的原理，数字图像经过数字卷积滤波处理，可以达到削减噪声信号、增强边界清晰度、提取某方向的信息等特殊效果。下图显示数字卷积滤波的过程。

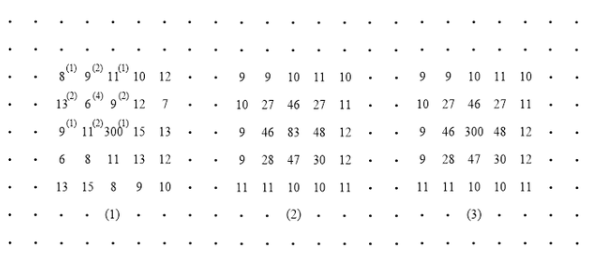
数字卷积滤波过程示意图

上图为一数字图像的部分数据，每个数字表示像素的灰度值，其中的部分数据和周围数据差异很大。其中带括号的数字共同组成了卷积滤波模板，它是一个奇数行奇数列的数字阵列，阵列中心成为卷积核心。

卷积滤波过程就是将卷积核心分别对应要处理的数值，卷积滤波模板的其它参数对应要处理数值周围的数值，把卷积滤波模板对应范围内的数值分别和卷积滤波模板内的参数相乘，然后再求这些乘积的代数和，最后除以卷积滤波模板的系数（卷积滤波模板内各参数的代数和），得到了处理后的数值，将此数值代替数字图像中卷积核心对应的数值，然后将卷积滤波模板移动一个像元，重复以上的计算，直到数字图像的每个像元都被处理完为止，处理后的部分数据如下图所示。观察处理的数据可以发现，异常数据对周围数据的影响体现得比较明显。用卷积滤波模板处理完数据以后，再把异常数据再重新赋值回去，这样既体现了异常点对周围数据的影响，又不改变它自身的既定数值。

将以上计算过程表达成一般的计算公式，可写作：

2、 分形理论

分形理论是研究复杂体系的新方法，它的核心思想是将一个存在某种精细结构自相似的随机复杂几何体，描述成有限阶分形的组合。

本着对复杂曲面分形描述，逐阶逼近的原则，我们可以将研究区域中所有样本点属性数据算术平均，该算术平均作为零阶分形的属性值，记做MDG［F0（0，0）］，当然这仅是研究区域最为粗略的描述。将研究区域分为m×n的子区域，通常每个子区域都包含着若干个样本点，逐个地对每个子区域内的样本点属性值取其算术平均，子区域中样本点属性平均值记做MDS［F1（i，j）］，F1（i，j）表示第i行（i＝0，1，2），第j列（j＝0，1，2）的第一阶分形子区域。考虑到本阶分形子区域是上阶分形子区域的局部，因为本阶分形子区域属性赋值要受到上阶分形子区域的影响。我们用加权平均解决，既：

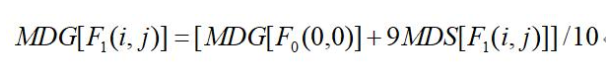
注意本阶分形子区域样本点属性平均值的权重我们取9，而上阶分形子区域的权重取1，突出当前阶分形子区域样本点属性平均值的作用。当然，这两个权重值是可以调整的。这样每个分形子区域（1阶分形就有91＝9个子区域）都赋有属性值。重复上面的做法，直到分形子区域的大小达到要求的网格大小为止。