关于波束斜视的量与角度θ和频率变化呈函数关系

关于相控阵天线方向图，我们将分三部分介绍，这是第二篇文章。在第一部分中（相控阵天线方向图：线性阵列波束特性和阵列因子），我们介绍了相控阵转向概念，并查看了影响阵列增益的因素。在第二部分，我们将讨论栅瓣和波束斜视。栅瓣很难可视化，所以我们利用它们与数字转换器中信号混叠的相似性，将栅瓣想象为空间混叠。接下来，我们探讨波束斜视的问题。波束斜视是我们使用相移，而不是使用真实时间延迟来使波束转向时，天线在频段范围内无聚焦的现象。我们还将讨论这两种转向方法之间的权衡取舍，并了解波束斜视对典型系统的影响。

栅瓣简介

到目前为止，我们只见过元件间隔为d = λ/2这种情况。图1开始说明为什么λ/2的元件间隔在相控阵中如此常见。图中共显示两种情况。首先，是蓝色线条，重复显示第1部分图11中的30°图。接下来，d/λ间隔增加到0.7，以显示天线方向如何变化。注意，随着间隔增加，波束宽度减小，这是一个积极现象。零值间隔减小使它们的距离更接近，这也可以接受。但是现在出现了第二个角度，在本例中为–70°，在该角度下出现了全阵列增益。这是最为不利的情况。这种天线增益复制被定义为一个栅瓣，可以被认为是空间混叠。

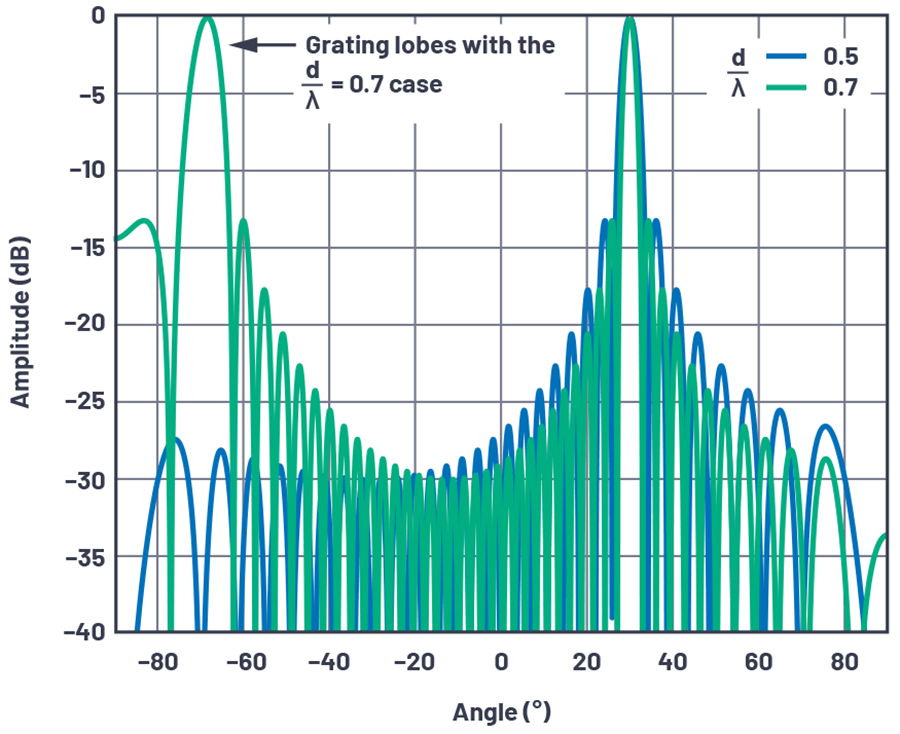
图1.在两种不同的d/λ间隔下，32元件线性阵列的标准化阵列因子。

采样系统的类比

为实现栅瓣可视化，可以将其类比为采样系统中的混叠现象。在模数转换器（ADC）中，接收器结构通常会对频率进行欠采样。欠采样包括有意降低采样率（fS），通过采样过程将高于fS/2的频率（较高的奈奎斯特区）转换为第一个奈奎斯特区的混叠。这使得这些较高频率看起来似乎在ADC输出端为较低频率。

可以考虑在相控阵中采用类似的类比方法，在该阵列中，由元件对波前进行空间采样。如果我们建议为了避免混叠，对每个波长实施两次采样（即元件），那么奈奎斯特准则可以扩展应用到空间区域。因此，如果元件间隔大于λ/2，我们可以考虑这种空间混叠。

计算栅瓣出现的位置

但是这些空间混叠（栅瓣）会出现在哪里？在第1部分中，我们展示了整个阵列中元件的相移与波束角度之间的函数关系。

反过来，我们可以根据与相移的函数关系来计算波束角度。

arcsin函数只产生-1和+1之间的实数解。在这些范围之外，无法得到实数解，电子数据表软件中会出现“#NUM！”。还要注意，方程2中的相位呈周期性，每隔2π重复一次。所以，我们可以使用（m × 2π + ∆Φ）取代波束转向公式中的∆Φ，进而得出公式3。

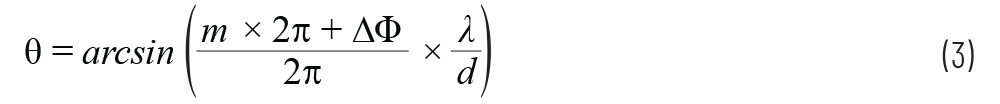
其中m = 0、±1、±2…

为了避免栅瓣，我们的目标是获得单一实数解。从数学上讲，这通过使下式成立来实现

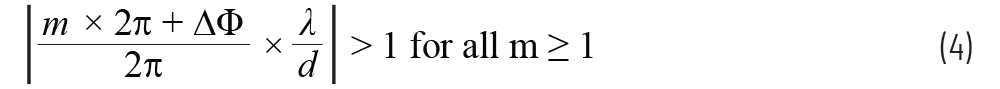
如果我们这样做，那么所有的空间图像（即m =±1、±2等）将产生非实数arcsin结果，我们可以忽略它们。但如果我们不能这样做，那么某些m 》 0的值会产生实数arcsin结果，那么我们会得出多个解：栅瓣。

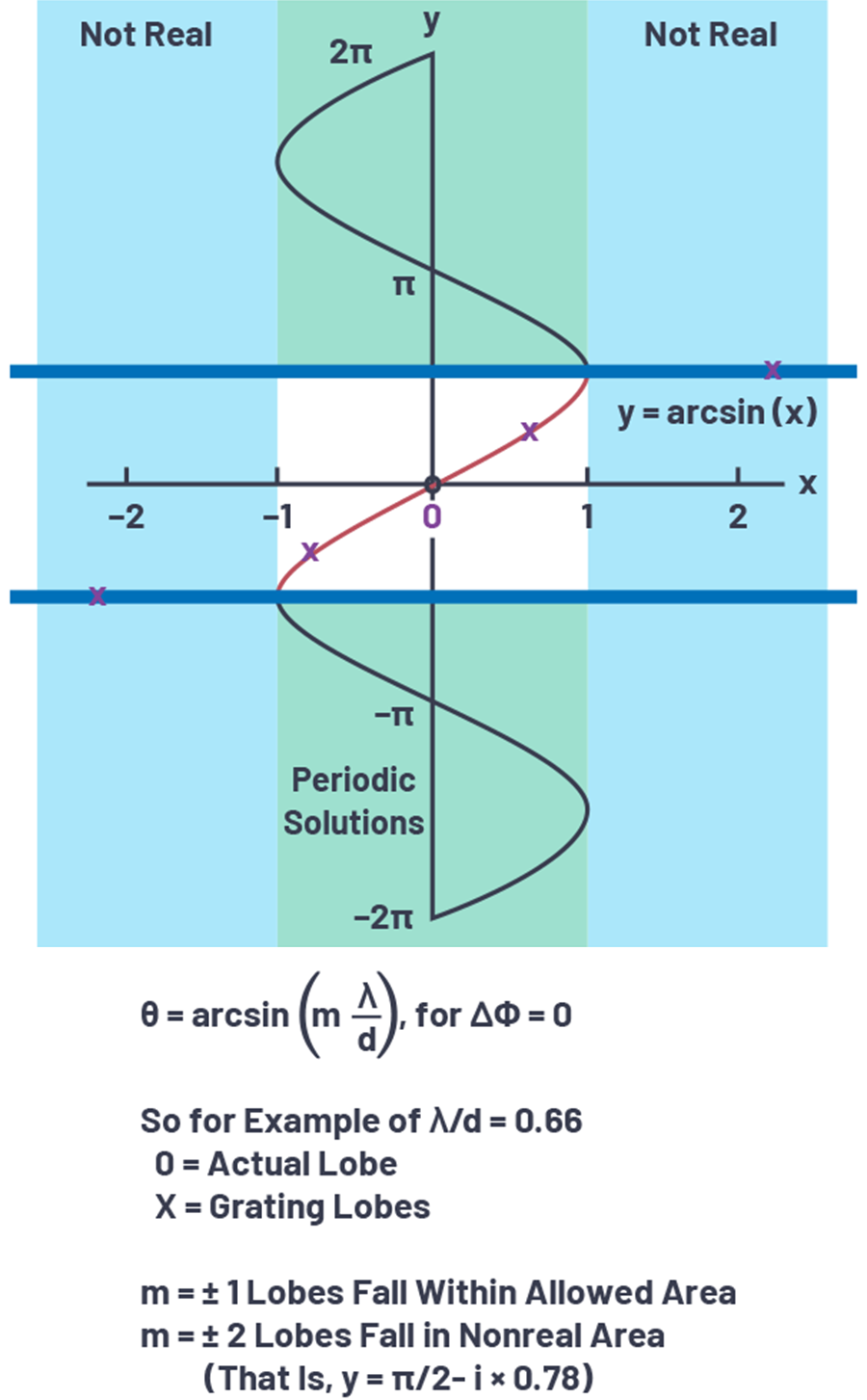
图2.arcsin函数在栅瓣中的应用。

d 》 λ和λ= 0°的栅瓣

让我们尝试通过一些示例来更好地说明这一点。首先，考虑机械轴线校准示例，其中θ= 0，所以∆Φ = 0。然后，将公式3简化为公式5。

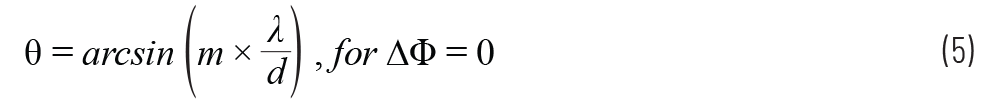
通过这种简化，可以明显看出，如果λ/d 》 1，那么只有当m = 0，才可以得出在–1和+1之间的参数。这个参数就是0，且arcsin（0） = 0°，也就是机械轴线校准角度。这就是我们期望获得的结果。此外，m ≥1时，arcsin参数会非常大（》1），不会得出实数结果。我们可以看到，θ= 0和d 《 λ时，没有栅瓣。

但是，如果d 》 λ（使得λ/d 《 1），则会存在多个解和栅瓣。例如，如果λ/d = 0.66（即d = 1.5λ），则m = 0和m = ±1时存在arcsin实数解。m = ±1是第二个解，是所需信号的空间混叠。因此，我们会看到三个主瓣，分别位于arcsin（0×0.66）、arcsin（1×0.66）和arcsin（-1×0.66），每个的振幅都大约相等。如果用度数表示，这些角度为0°和±41.3°。事实上，这就是图3中的阵列因子图所示的内容。

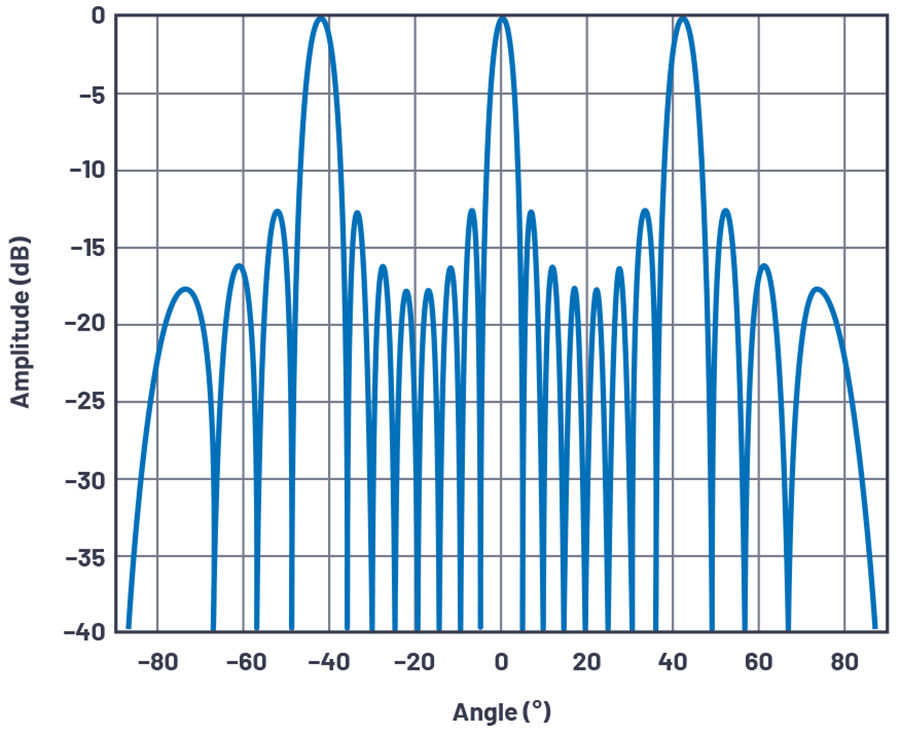
图3.d/λ= 1.5、N = 8时，轴线校准的阵列因子。

λ/2 《 d 《 λ时的栅瓣

在简化栅瓣方程（方程5）时，我们选择只看机械轴线校准（∆Φ= 0）。我们还看到，在机械轴线校准时，d 《 λ时不会出现栅瓣。但是从采样理论类比中，我们知道，当间隔大于λ/2时，会出现一些类型的栅瓣。所以，当λ/2 《 d 《 λ时，栅瓣在什么位置？

首先，回顾一下在第1部分的图4中，相位是如何随转向角度变化的。我们看到，当主瓣偏离机械轴线校准时，∆Φ的范围为0至±π。因此，

的范围为

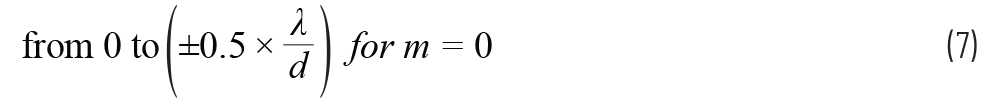
|m|≥1时，其值则超出该范围

如果我们想要在所有|m| ≥1的情况下，保持整个arcsin参数》 1，则会限制最小可允许的λ/d。考虑两种情况：

· 如果λ/d ≥2（即d ≤ λ/2），则无论m的值为多少，都不会出现多个解。m 》 0的所有解都会导致arcsin参数》 1。这是唯一避免水平方向出现栅瓣的方法。

· 但是，如果我们有意将∆Φ限制为小于±π，那么我们可以接受较小的λ/d，且不会出现栅瓣。减小∆Φ的范围意味着减小阵列的最大转向角度。这是一种有趣的权衡，将在下一节中探讨。

元件间隔考虑

元件间隔是否应该始终小于λ/2？并非如此！这就是天线设计人员需要作出的考虑和权衡。如果波束完全被转到水平方向，且θ= ±90°，则需要元件间隔为λ/2（如果可见的半圆内不允许出现栅瓣）。但在实际操作中，可实现的最大转向角度总是小于90°。这是由于元件因子，以及在大转向角度下的其他降低引起的。

从图2所示的arcsin图中，我们可以看出，如果y轴θ限制为减小的限值，则栅瓣只在不会使用的扫描角度下出现。对于给定的元件间隔（dmax）来说，这种减小的限值（θmax）是多少？我们之前说过，我们的目标是使下式成立

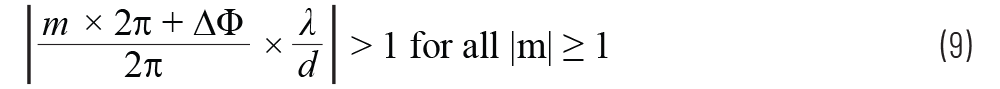
我们可以用它来计算第一个栅瓣（m =±1）出现的位置。现在使用第1部分用于∆Φ的公式1，得出：

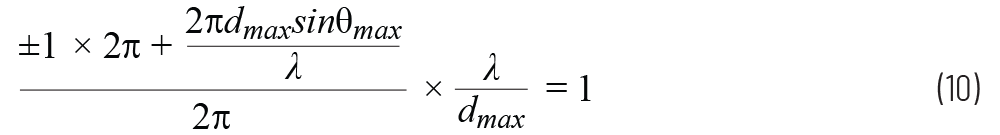
可以简化为

然后得出dmax

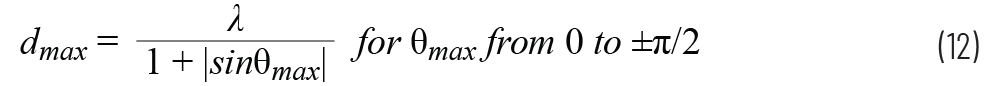
该dmax 是在减小的扫描角度（θmax）下没有栅瓣的条件，其中θmax小于π/2 （90°）。例如，如果信号频率为10 GHz，我们需要在没有栅瓣的情况下转向±50°，则最大元件间隔为：

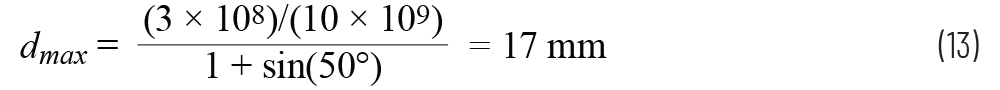
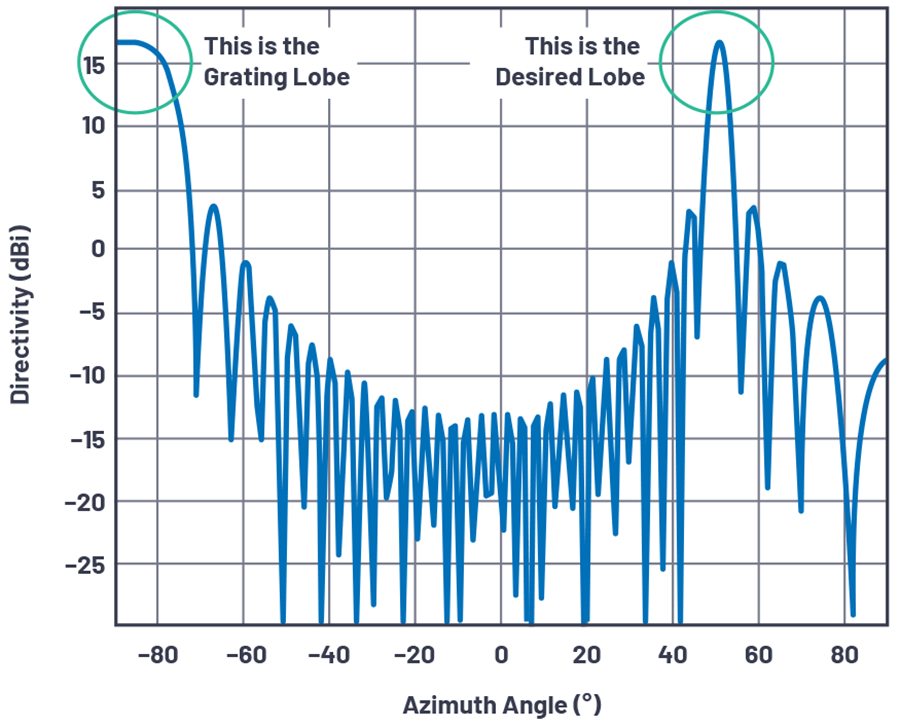
图4.θ= 50°、N = 32、d = 17 mm且Φ= 10 GHz时，栅瓣开始在水平方向出现。

通过限制最大扫描角度，可以自由地扩展元件间隔，增加每个通道的物理尺寸，以及扩展给定数量的元件的孔径。例如，可以利用这个现象，为天线分配相当狭窄的预定义方向。元件增益可以增大，以在预先定义的方向上提供方向性，元件间隔也可以增大，以实现更大孔径。这两种方法都能在较窄的波束角度下获得较大的整体天线增益。

注意，方程3表示最大间隔为一个波长，即使在零转向角度下也是如此。在一些情况下，如果栅瓣不出现在可见半圆内即可。以地球同步卫星为例，会以机械轴线校准为中心，按9°的转向角度覆盖整个地球。在这种情况下，只要栅瓣不落在地球表面就可以。因此，元件间隔可以达到几个波长，使得波束宽度更窄。

还有一些值得注意的天线结构，试图通过形成不一致的元件间隔来克服栅瓣问题。这些被归类为非周期阵列，以螺旋阵列为例。由于机械天线构造的原因，我们可能希望有一个通用的可以扩展为更大阵列的构建模块，但是，这会形成一致的阵列，会受所述的栅瓣条件影响。

波束斜视

在第1部分中，我们开头描述了在波峰接近元件阵列时，如何基于相对于轴线校准的波峰角度θ在元件之间出现时间延迟。对于单一频率，可以用相移代替时间延迟来实现波束转向。这种方法适用于窄带波形，但对于通过相移产生波束转向的宽带波形，波束可能转移方向（与频率呈函数关系）。如果我们记得时间延迟是线性相移与频率之间的关系，则可以直观地解释。所以，对于给定的波束方向，要求相移随频率变化。或者相反，对于给定的相移，波束方向随频率变化。波束角度随频率变化的状况，被称为波束斜视。

还考虑到在轴线校准位置θ= 0时，没有跨元件的相移，因此不会产生任何波束斜视。因此，波束斜视的量必须与角度θ和频率变化呈函数关系。图5显示一个X频段示例。在本例中，中心频率为10 GHz，调制带宽为2 GHz，且很显然波束随频率和初始波束角度的变化而改变方向。

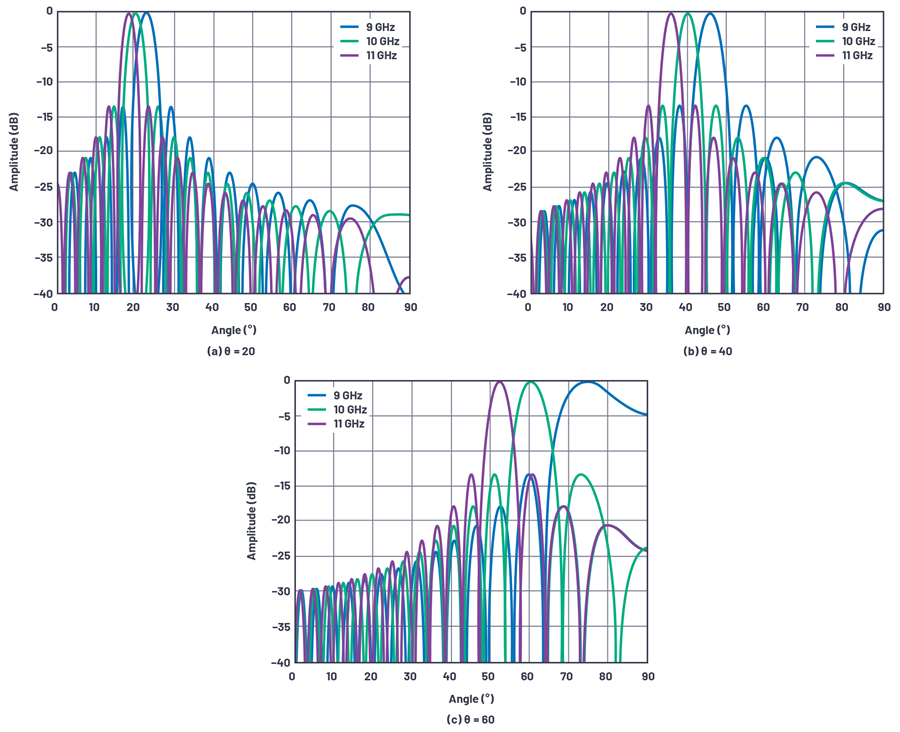
图5.32元件线性阵在元件间隔为λ/2时，在X频段上的波束斜视示例。

波束斜视可以直接计算。使用公式1和公式2，可以计算得出波束方向偏差和波束斜视

此公式如图6所示。在图6中，显示的f/f0比率是有意的。前一个方程的倒数（f0/f）提供了一种更容易的方法，可以更直观地表示相对于中心频率的变化。

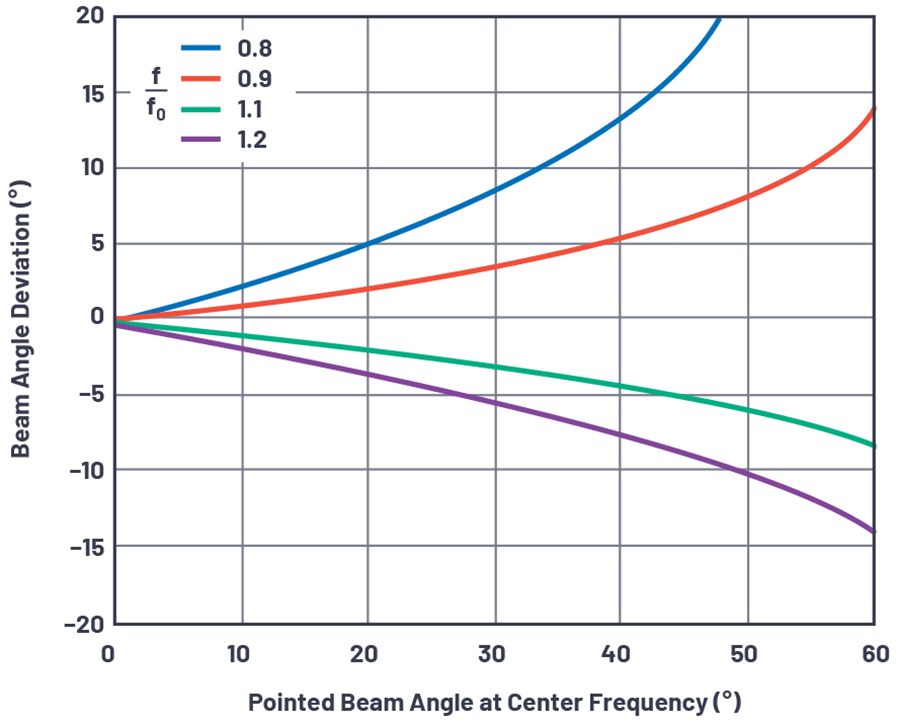
图6.几种频率偏差下的波束斜视和波束角度。

关于波束斜视的几点观察发现：

· 波束角度与频率的偏差随着波束角度偏离轴线校准的角度增大而增大。

· 低于中心频率的频率比高于中心频率的频率产生更大的偏差。

· 低于中心频率的频率会使波束更加远离轴线校准。

波束斜视考虑

波束斜视，即转向角度与频率的偏差，是由相移来实现时间延迟造成的。用真实时间延迟单元来执行波束转向则不会出现此问题。

既然波束斜视问题如此明显，为什么还有人使用移相器，而不是时间延迟单元呢？一般而言，这归因于设计简单，以及移相器和时间延迟单元的IC可用性。时间延迟以某些传输线的形式实现，所需的总延迟时间与孔径大小呈函数关系。到目前为止，大多数可用的模拟波束成型IC都是基于相移，但也出现了一些真实时间延迟IC系列，它们在相控阵中更加常见。

在数字波束成型中，真实时间延迟可以采用DSP逻辑和数字波束成型算法实现。因此，对于每个元件都数字化的相控阵架构，它本身就可以解决波束斜视问题，并提供最高的编程灵活性。但是，这种解决方案的功能、尺寸和成本都会造成问题。

在混合波束成型中，子阵采用模拟波束成型，全阵采用数字波束成型。这可以提供一些值得考虑的波束斜视减少。波束斜视只受子阵影响，子阵的波束宽度更宽，因此对波束角度偏差的容忍度更大。因此，只要子阵的波束斜视是可容忍的，即可在后接真实时间延迟（数字波束成型）的子阵内采用带移相器的混合波束成型结构。

总结

以上就是有关相控阵天线方向图三部分中的第2部分内容。在第1部分，我们介绍了波束指向和阵列因子。在第2部分，我们讨论栅瓣和波束斜视的缺点。在第3部分，我们将讨论如何通过天线变窄缩小旁瓣，并让您深入了解移相器量化误差。
责任编辑:pj