解决量子神经网络消失梯度问题 更好利用 NISQ 设备资源

文 /大众汽车公司和莱顿大学的 Andrea Skolik

3 月初，Google 与滑铁卢大学和大众汽车公司共同发布了 TensorFlow Quantum(TFQ)。TensorFlow Quantum 是一个量子机器学习 (QML) 软件框架，允许研究员联合使用 Cirq 和 TensorFlow 的功能。Cirq 和 TFQ 都用于模拟噪声中等规模量子 (NISQ) 的设备。这些设备当前仍处于实验阶段，因此未经纠错，还会受到噪声输出的影响。

本文介绍的训练策略可以解决量子神经网络 (QNN) 中的消失梯度问题，并更好地利用 NISQ 设备提供的资源。

量子神经网络

训练 QNN 与训练经典神经网络没有太大不同，区别仅在于优化量子电路的参数而不是优化网络权重。量子电路的外形如下所示：

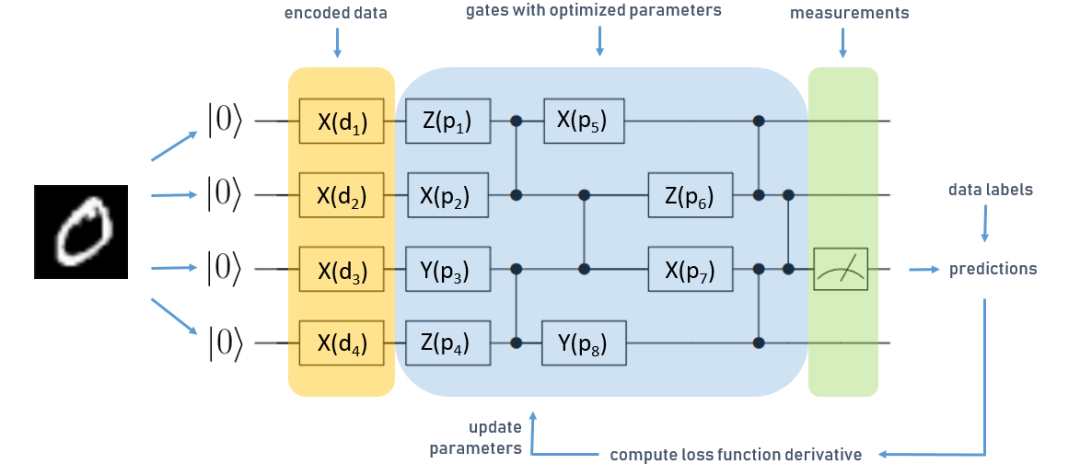
用于四个量子位分类任务的简化 QNN

电路从左到右读取，每条水平线对应量子计算机寄存器中的一个量子位，每个量子位都初始化为零状态。方框表示对按顺序执行的量子位的参数化运算（或“门”）。在这种情况下，我们有三种不同类型的运算，X、Y 和 Z。垂直线表示两个量子逻辑门，可用于在 QNN 中产生纠缠 - 一种使量子计算机胜过经典计算机的资源。我们在每个量子位上将一层表示为一个运算，然后将一系列的门连接成对的量子位，产生纠缠。

上图为用于学习 MNIST 数字分类的简化 QNN。

首先，将数据集编码为量子态。使用数据编码层来完成这一操作，上图中标记为橙色。在这种情况下，我们将输入数据转换为向量，并将向量值用作数据编码层运算的参数 d 。基于此输入执行电路中蓝色标记的部分，这一部分代表 QNN 的可训练门，用 p表示。

量子电路的最后一个运算是测量。计算期间，量子设备对经典位串的叠加执行运算。当我们在电路上执行读出时，叠加状态坍缩为一个经典位串，这就是最后的计算输出。所谓的量子态坍缩是概率性的，要获得确定性结果，我们需要对多个测量结果取平均值。

上图中，绿色标记的部分是第三个量子位上的测量，这些测量结果用于预测 MNIST 样本的标签。将其与真实数据标签对比，并像经典神经网络一样计算损失函数的梯度。由于参数优化是经典计算机使用 Adam 等优化器处理，因此这些类型的 QNN 称为“混合量子经典算法”。

消失的梯度，又称贫瘠高原

事实证明，QNN 与经典神经网络一样，也存在消失梯度的问题。由于 QNN 中梯度消失的原因与经典神经网络有着本质的不同，因此采用了一个新术语：贫瘠高原 (Barren Plateaus)。本文不探讨这一重要现象的所有细节，建议感兴趣的读者阅读首次介绍 QNN 训练景观 (Training Landscapes) 中贫瘠高原的文章。

简而言之，当量子电路被随机初始化，就会出现贫瘠高原 - 在上述电路中，这意味着随机选择运算及其参数。这是训练参数化量子电路的一个重点问题，并且会随着量子位数量和电路中层数的增加而越发严重，如下图所示。

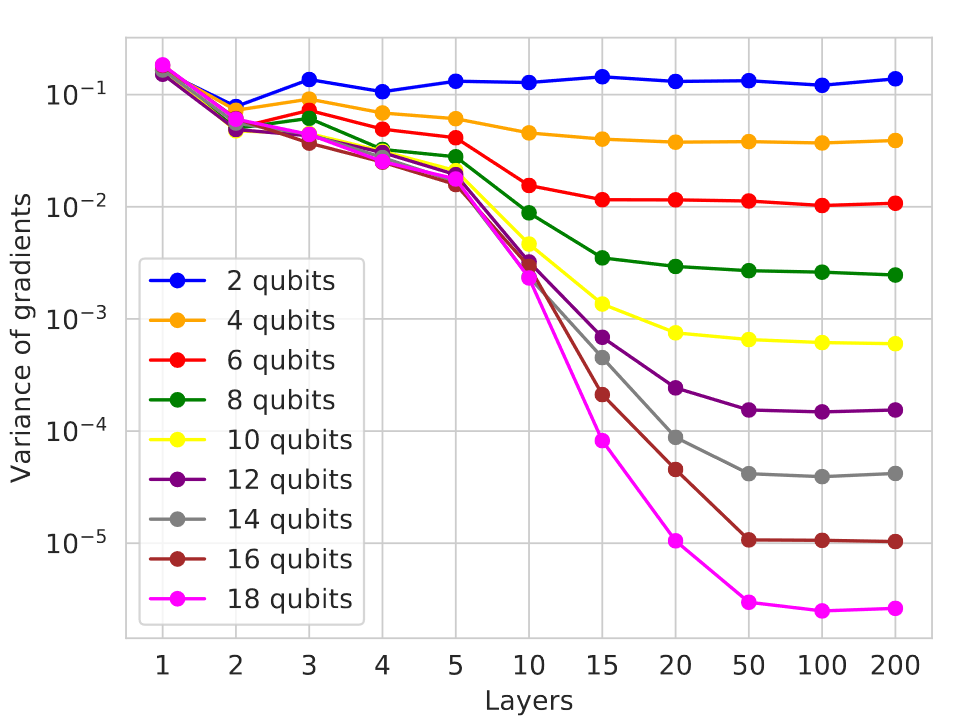
梯度方差根据随机电路中量子位和层数的变化而衰减

对于下面介绍的算法，关键在于电路中添加的层越多，梯度的方差就越小。另一方面，类似于经典神经网络，QNN 的表示能力也随着深度的增加而增加。这里的问题是，随着电路尺寸的增加，优化景观在很多位置都会趋于平坦，以至于难以找到局部最小值。

注意，对于 QNN，输出通过多次测量的平均值进行估算。想要估算的量越小，获得准确结果所需的测量就越多。如果这些量与测量不确定性或硬件噪声造成的影响相比要小得多，这些量就无法可靠确定，电路优化基本上会变成随机游走。

为了成功训练 QNN，必须避免参数的随机初始化，同时也要阻止 QNN 在训练过程中由于梯度变小而随机化，例如在接近局部最小值的时候。为此，我们可以限制 QNN 的架构（例如，通过选择某些门配置，这需要根据当前任务调整架构），或控制参数的更新，使其不会变得随机。

分层学习

在我们与 Volkswagen Data:Lab（Andrea Skolik、Patrick van der Smagt、Martin Leib）和 Google AI Quantum（Jarrod R. McClean、Masoud Mohseni）网络联合发表的论文 Layerwise learning for quantum neural networks 中，我们介绍了一种避免初始化在高原上并避免网络在训练过程中在高原上结束的方法。接下来是一个关于 MNIST 数字二进制分类学习任务的分层学习 (Layerwise Learning) 示例。首先，我们需要定义待堆叠的层的结构。当前的学习任务未经任何假设，因此各层选择的布局与上图相同：一层由每个初始化为零的量子位上的随机门和两个量子逻辑门组成，两个量子逻辑门连接量子位以实现纠缠。

我们指定了若干个起始层，在本例中只有一个，将在训练过程中始终保持活跃状态，并指定训练每组层的周期数。另外两个超参数是每个步骤中添加的新层数，以及一次被最大训练的层数。在这里选择一种配置，其中每个步骤中添加两个层，并冻结除起始层之外的所有先前层的参数，以在每个步骤中仅训练三个层。将每组层训练 10 个周期，然后重复此过程十次，直到电路总共由 21 层组成。这里的事实依据是浅层电路会比深层电路产生更大梯度，由此避免了高原上的初始化。

这提供了一个优化过程的良好起点，可以继续训练更大的连续层集。对另一个超参数，我们定义了算法第二阶段一起训练的层的百分比。在此将电路分成两半，交替训练两个部分，其中不活动部分的参数始终冻结。一个所有分区都训练过一次的训练序列称为扫描，对这个电路执行扫描，直到损失收敛。当完整参数集始终完成训练时，我们将这种情况称为“完全深度学习”(Complete Depth Learning)，一个欠佳的更新步骤会影响整个电路并将其引入随机配置，导致无从逃脱的贫瘠高原。

接下来将我们的训练策略与训练 QNN 的标准技术 CDL 进行比较。为了得到公平的结果，我们使用与先前 LL 策略生成的电路架构完全相同的电路架构，但现在在每一步中同时更新所有参数。为了给 CDL 提供训练的机会，参数将优化为零，而不是随机优化。由于无法使用真正的量子计算机，因此我们模拟 QNN 的概率输出，并选择一个相对较低的值来估计 QNN 每次预测的测量次数——此例中为 10。假设真正的量子计算机上的采样率为 10kHZ，我们可以估算出训练运行的实验性挂钟时间，如下所示：

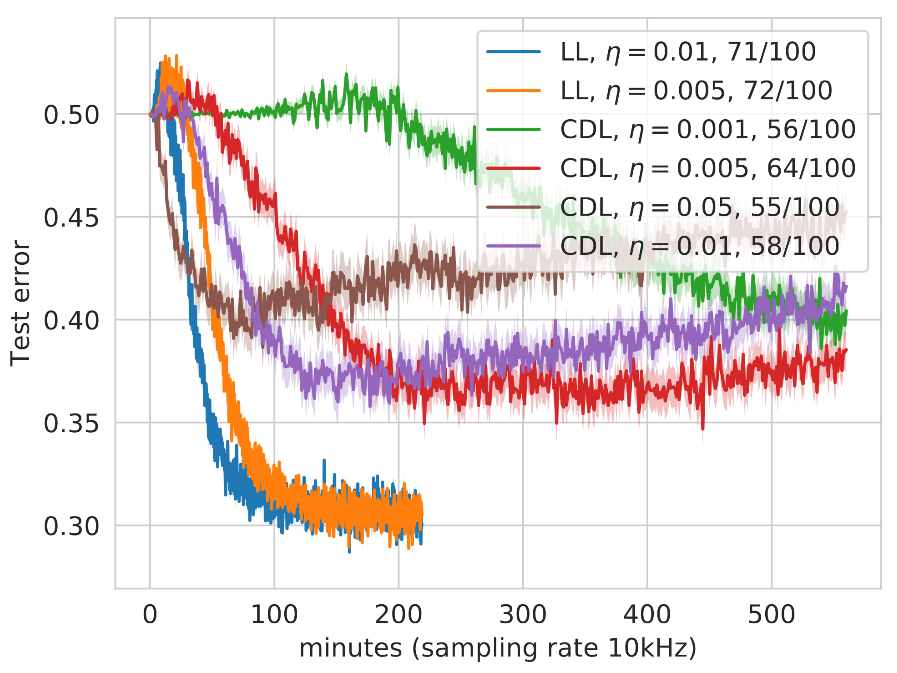
不同学习率 η 的分层深度学习和完全深度学习的比较。每种配置训练了 100 个电路，并对最终测试误差低于 0.5（图例中成功运行的次数）的电路取平均值

通过少量的测量，可以研究 LL 和 CDL 方法不同梯度幅度的影响：如果梯度值较大，则与较小值相比，10 次测量可以提供更多信息。执行参数更新的信息越少，损失的方差就越大，执行错误更新的风险也就越大，这将使更新的参数随机化，并导致 QNN 进入高原。这一方差可以通过更小的学习率降低，因此上图比较了学习率不同的 LL 和 CDL 策略。

值得注意的是，CDL 运行的测试误差会随运行时间的增加而增加，最初看起来像是过拟合。然而，这张图中的每条曲线都是多次运行的平均值，实际情况是，越来越多的 CDL 运行在训练过程中随机化，无法恢复。如图例所示，与 CDL 相比，LL 运行中有更大一部分在测试集上实现了小于 0.5 的分类误差，所用时间也更少。

综上所述，分层学习提高了在更少训练时间内成功训练 QNN 的概率，总体上具有更好的泛化误差，这在 NISQ 设备上尤其实用。
原文标题：介绍量子神经网络训练策略，解决消失梯度问题

文章出处：【微信公众号：TensorFlow】欢迎添加关注！文章转载请注明出处。