从智能手机到航天器,机器学习算法无处不在。他们会告诉您明天的天气预报,将一种语言翻译成另一种语言,并建议您接下来想在设备上看什么电视连续剧。这些算法会根据数据自动调整(学习)其内部参数。但是,有一部分参数是无法学习的,必须由专家进行配置。这些参数通常被称为“超参数”,随着AI的使用增加,它们对我们的生活产生重大影响。
例如,决策树模型中的树深度和人工神经网络中的层数是典型的超参数。模型的性能在很大程度上取决于其超参数的选择。对于中等深度的树,决策树可能会产生良好的结果,而对于非常深的树,决策树的性能将很差。如果我们要手动运行,最佳超参数的选择更是艺术性。实际上,超参数值的最佳选择取决于当前的问题。
由于算法,目标,数据类型和数据量从一个项目到另一个项目都发生了很大变化,因此没有适合所有模型和所有问题的超参数值的最佳选择。相反,必须在每个机器学习项目的上下文中优化超参数。
在本文中,我们将从回顾优化策略的功能开始,然后概述四种常用的优化策略:
- 网格搜索
- 随机搜寻
- 爬山
- 贝叶斯优化
- 优化策略
即使有专家深入的领域知识,手动优化模型超参数的任务也可能非常耗时。另一种方法是让专家离开,并采用自动方法。根据某种性能指标来检测给定项目中给定模型的最佳超参数集的自动过程称为优化策略。
典型的优化过程定义了可能的超参数集以及针对该特定问题要最大化或最小化的度量。因此,实际上,任何优化过程都遵循以下经典步骤:
1)将手头的数据分为训练和测试子集
2)重复优化循环固定次数或直到满足条件:
a)选择一组新的模型超参数
b)使用选定的超参数集在训练子集上训练模型
c)将模型应用于测试子集并生成相应的预测
d)使用针对当前问题的适当评分标准(例如准确性或平均绝对误差)评估测试预测。存储与选定的超参数集相对应的度量标准值
3)比较所有度量值,然后选择产生最佳度量值的超参数集
问题是如何从步骤2d返回到步骤2a,以进行下一次迭代。也就是说,如何选择下一组超参数,确保它实际上比上一组更好。我们希望优化循环朝着合理的解决方案发展,即使它可能不是最佳解决方案。换句话说,我们要合理确定下一组超参数是对上一组的改进。
典型的优化过程将机器学习模型视为黑匣子。这意味着在每个选定的超参数集的每次迭代中,我们感兴趣的只是由选定指标测量的模型性能。我们不需要(想要)知道黑匣子内部发生了什么变化。我们只需要转到下一个迭代并迭代下一个性能评估,依此类推。
所有不同优化策略中的关键因素是如何根据步骤2d中先前的度量标准输出,在步骤2a中选择下一组超参数值。因此,对于一个简化的实验,我们省略了对黑盒的训练和测试,我们专注于度量计算(数学函数)和选择下一组超参数的策略。此外,我们用任意数学函数替换了度量计算,并用函数参数替换了一组模型超参数。
通过这种方式,优化循环运行得更快,并尽可能保持通用。进一步的简化是使用仅具有一个超参数的函数,以实现简单的可视化。下面是我们用来演示四种优化策略的函数。我们想强调的是,任何其他数学函数也可以起作用。
f(x)= sin(x / 2)+0.5⋅sin(2⋅x)+0.25⋅cos(4.5⋅x)
这种简化的设置使我们可以在一个简单的xy图上可视化一个超参数的实验值和相应的函数值。在x轴上是超参数值,在y轴上是函数输出。然后,根据描述超参数序列生成中的点位置的白红色渐变对(x,y)点进行着色。
白点对应于该过程中较早生成的超参数值。红点对应于此过程中稍后生成的超参数值。此渐变着色将在以后用于说明优化策略之间的差异时很有用。在这种简化的用例中,优化过程的目标是找到一个使函数值最大化的超参数。让我们开始回顾四种常见的优化策略,这些策略用于为优化循环的下一次迭代标识新的超参数值集。
这是基本的蛮力策略。如果您不知道尝试使用哪些值,则可以全部尝试。功能评估中使用固定步长范围内的所有可能值。
例如,如果范围为[0,10],步长为0.1,那么我们将获得超参数值的序列(0、0.1、0.2、0.3,…9.5、9.6、9.7、9.8、9.9、10) 。在网格搜索策略中,我们为这些超参数值的每一个计算函数输出。因此,网格越细,我们越接近最优值,但是所需的计算资源也就越高。
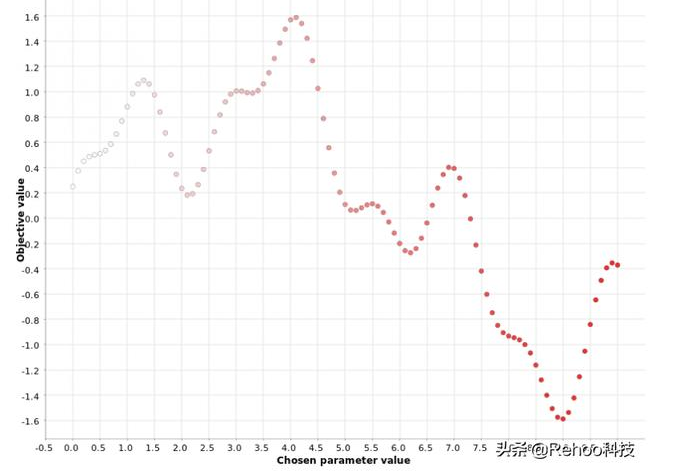
使用步骤0.1在[0,10]范围内对超参数值进行网格搜索。颜色梯度反映了在生成的超参数候选序列中的位置。白点
如图所示,从小到大扫描超参数的范围。网格搜索策略在单个参数的情况下可以很好地工作,但是当必须同时优化多个参数时,它的效率将非常低下。
随机搜寻
对于随机搜索策略,顾名思义,超参数的值是随机选择的。在多个超参数的情况下,通常首选此策略,并且当某些超参数对最终指标的影响大于其他参数时,此策略特别有效。
同样,在[0,10]范围内生成超参数值。然后,随机生成固定数量的超参数。可以使用固定数量的预定义超参数进行试验,您可以控制此优化策略的持续时间和速度。N越大,达到最佳状态的可能性越高,但是所需的计算资源也就越高。

在[0,10]范围内随机搜索超参数值。颜色梯度反映了在生成的超参数候选序列中的位置。白点对应于过程中较早
不出所料,来自生成序列的超参数值没有降序或升序使用:白色和红色点在图中随机混合。
爬山
在爬坡,在每次迭代的方式选择在超参数空间选择下一个超参数值的最佳方向。如果没有相邻改善最终指标,则优化循环将停止。
请注意,此过程在一个重要方面与网格搜索和随机搜索不同:选择下一个超参数值时要考虑先前迭代的结果。
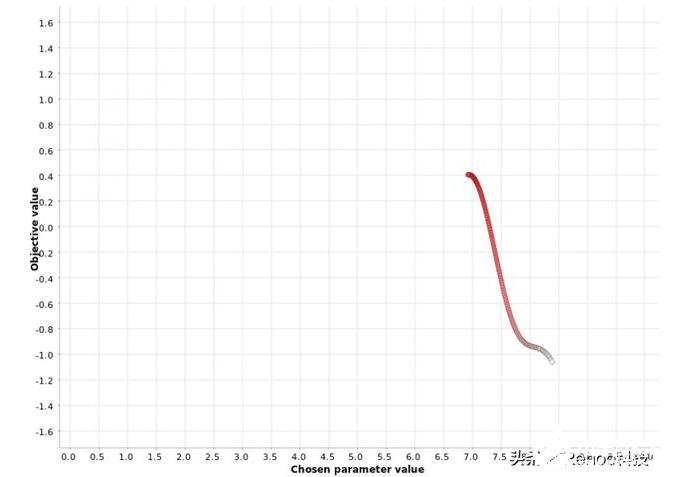
在[0,10]范围内对超参数值进行爬山搜索。颜色梯度反映了在生成的超参数候选序列中的位置。白点对应于过程
上图显示了应用于我们函数的爬坡策略从一个随机的超参数值x = 8.4开始,然后在x = 6.9时朝函数最大值y = 0.4移动。一旦达到最大值,就不会在下一个邻居中看到度量值的进一步增加,并且搜索过程将停止。
此示例说明了与此策略有关的警告:它可能陷入次要最大值。从其他图中可以看出,全局最大值位于x = 4.0处,对应的度量值为1.6。该策略找不到全局最大值,但陷入局部最大值。此方法的一个很好的经验法则是以不同的起始值多次运行它,并检查算法是否收敛到相同的最大值。
贝叶斯优化
该贝叶斯优化战略选择基于以前的迭代,类似于爬山策略的功能输出的下一个超参数值。与爬山不同,贝叶斯优化会全局查看过去的迭代,而不仅仅是最后一次。
此过程通常分为两个阶段:
在称为预热的第一阶段中,将随机生成超参数值。在用户定义的数量N个此类超参数的随机生成之后,第二阶段开始。
在第二阶段中,在每次迭代中,都会估计类型为P(输出|过去超参数)的“替代”模型,以描述输出值在过去迭代中对超参数值的条件概率。该替代模型比原始函数更容易优化。因此,该算法优化了替代,并建议将替代模型的最大值处的超参数值也作为原始函数的最佳值。第二阶段的一小部分迭代还用于探测最佳区域之外的区域。这是为了避免局部最大值的问题。
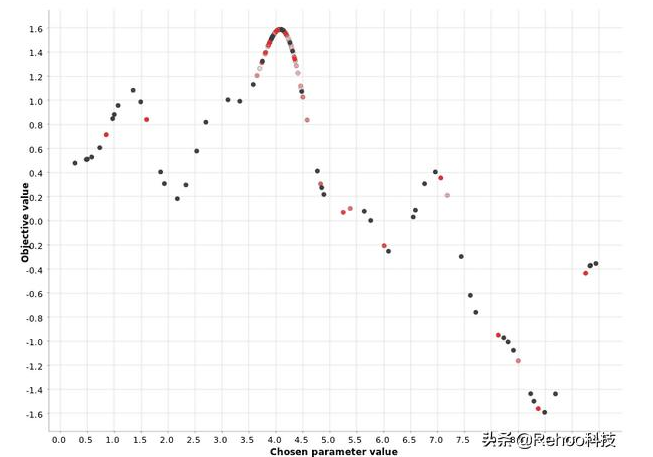
[0,10]范围内超参数值的贝叶斯优化。颜色梯度反映了在生成的超参数候选序列中的位置。白点对应于过程中较
上图图证明了贝叶斯优化策略使用预热阶段来定义最有希望的区域,然后为该区域中的超参数选择下一个值。您还可以看到,密集的红色点聚集在更接近最大值的位置,而淡红色和白色的点则分散了。这表明,第二阶段的每次迭代都会改善最佳区域的定义。
总结
我们都知道训练机器学习模型时超参数优化的重要性。由于手动优化非常耗时并且需要特定的专家知识,因此我们探索了四种常见的超参数优化自动过程。
通常,自动优化过程遵循迭代过程,在该过程中,每次迭代时,都会在一组新的超参数上训练模型,并在测试集上进行评估。最后,将与最佳度量得分相对应的超参数集选择为最佳集。问题是如何选择下一组超参数,以确保它实际上比上一组更好。
我们概述了四种常用的优化策略:网格搜索,随机搜索,爬山和贝叶斯优化。它们都各有利弊,我们通过说明它们在简单用例中的工作方式来简要解释了它们之间的差异。现在,您都可以尝试在现实中的机器学习问题中进行尝试。
-
神经网络
+关注
关注
42文章
4772浏览量
100852 -
机器学习
+关注
关注
66文章
8422浏览量
132739 -
决策树
+关注
关注
3文章
96浏览量
13561
发布评论请先 登录
相关推荐
被问爆的四种供电方式,来啦~
双轴测径仪的四种样式!
滤波电路的四种类型是什么
负反馈的四种类型是什么
pwm脉宽调制的四种方法有哪些
简述四种基本触发器及其功能
深度神经网络(DNN)架构解析与优化策略
介绍MCUboot支持的四种升级模式(2)





 机器学习四种常用的优化策略解析
机器学习四种常用的优化策略解析










评论