尽管因果关系经常用相对论和量子力学来讨论,但是这个思想在任何动力学系统中都是至关重要的。PCB互连是因果系统,准确建模PCB互连需要考虑信号行为和系统响应的特定方面。
如果可以正确建模信号的因果行为,则可以计算互连中的正确响应。这对于正确预测互连阻抗,脉冲响应和损耗至关重要。信号行为的所有这些方面对于高速互连至关重要,在高速互连中,信号带宽很容易跨越GHz范围。
因果系统和因果模型
因果系统被定义为仅在刺激发生之后而不是之前对外部刺激做出响应。只要正确定义了频域和时域行为,标准集总元件传输线模型就会在驱动线路时产生因果信号响应。在将互连建模为在t = 0之前具有零振幅的情况下,这里的关键方面。换句话说,您将Heaviside阶跃函数用作注入信号的加权函数。
就个人而言,我更喜欢在Laplace或Fourier域中工作,因为很容易定义各种功能的转换。考虑因果关系的标准技术是根据系统所需的脉冲响应函数或阶跃响应函数,确定互连在任一域中的传递函数。如果没有正确定义系统的传递函数,那么脉冲和阶跃响应可能会表现出无因果行为,这意味着信号会在驱动器切换之前开始在互连上传播!
信号处理界已经知道了数十年,但是PCB设计界也应该意识到在互连行为建模中这些潜在的非因果问题。互连的因果传递函数与其脉冲响应函数h(t)之间的关系是:
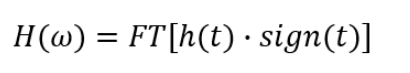
因果传递函数及其与互连的脉冲响应函数的关系。
这意味着,如果知道系统所需的因果冲激响应函数,则可以计算系统的传递函数。这将使用卷积定理完成,并产生一对Kramers-Kronig关系。请注意,如果已知互连的传递函数,则可以使用傅立叶逆变换恢复脉冲响应函数h(t)并检查它是否确实是因果的。对互连的传递函数建模不正确将导致对信号行为的建模不正确。通常情况下,直到您工作于〜5 GHz信号带宽之外,这种情况才会变得明显。这应该说明正确描述互连的脉冲响应的重要性,

PCB互连中因果和非因果响应的示例。
阻抗控制的因果模型
给定频率下的精确阻抗控制需要对因果系统中的介电常数进行精确建模。如果您在足够宽的频率范围内观察,则 任何材料都会具有一定的色散。很难在较宽的范围内找到关于折射率的实部和虚部的全套数据。假设您可以从文献或测量中访问此数据。在这种情况下,您可以使用这些值来计算有效阻抗的阻抗,例如,有效介电常数是在宽频带上在微带走线上传播的信号所看到的。
这样,您就可以在存在介电弥散的情况下为走线提供特征阻抗。类似的过程可以用于其他传输线几何形状。无论您是使用标准走线阻抗公式(微带 或 带状线)从有效的(取决于频率的)介电常数计算阻抗,还是提取板中的寄生效应 作为频率的函数,都可以计算出特性阻抗与频率的关系。此外,您还需要根据频率来确定损耗。如果您查看传输线模型中的寄生虫并计算寄生虫的频率依赖性,则这会更直观。

一个简单的示例,显示了FR4中的典型色散行为及其对微带走线的单端阻抗的影响。
另一种选择是使用一个模型,该模型根据少量测量来定义电介质(实部和虚部)的频率响应。在高级激光物理课程中教授的典型方法是使用Kramers-Kronig关系。当已知系统中的因果响应时,这对耦合积分被广泛用于描述系统的因果响应,或者,当已知系统中的因果响应时,这对耦合积分可用于计算损耗。另一种方法是使用标准模型,该模型定义相对介电常数的拟合轮廓。然后从有限数量的测量中确定定义拟合曲线的参数。宽带Debye模型被广泛认为是对PCB基板(尤其是PTFE层压板和FR4)中的分散进行建模的最精确模型。
关于因果关系的更多信息
请注意,我们仅查看了因果单端传输线的特征阻抗。我们也没有考虑过孔对因果模型中损耗的影响。因为附近的传输线可以感应和电容耦合由于这两种耦合方式都取决于频率,因此偶数和奇数模式阻抗(以及共模和差模阻抗)也将由于衬底中的色散而成为频率的函数。除了对基板中的分散进行建模之外,基板边缘处的铜粗糙度还有效地增加了迹线中的衰减,这也是趋肤效应导致的频率的函数。典型的处理方法是通过调用表面粗糙度因子(KSR)来重写互连上的总插入损耗,如下所示:

互连中的总插入损耗,粗糙度随频率变化。
将铜粗糙度影响作为频率和互连因果关系的函数进行建模仍然是研究的活跃领域。一个相关的主题是PDN的因果行为,因为这对于正确描述寄生对电源完整性的影响非常重要。随着越来越多的常见设备被迫以更高的速度运行,并且随着越来越多的设计人员开始在微波/毫米波范围内工作,用于将互连正确描述为因果系统的工具对于信号完整性至关重要。
编辑:hfy
-
pcb
+关注
关注
4319文章
23083浏览量
397552 -
信号
+关注
关注
11文章
2790浏览量
76732 -
因果系统
+关注
关注
0文章
2浏览量
6947
发布评论请先 登录
相关推荐

一文了解金属互连中阻挡层
一种基于因果路径的层次图卷积注意力网络
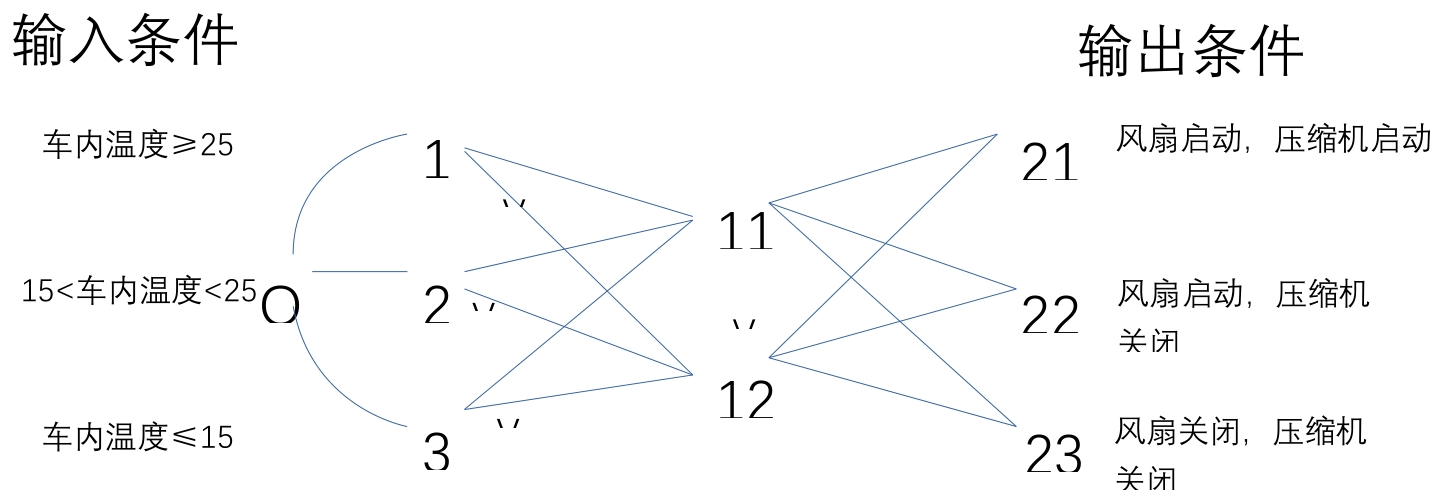
鉴源实验室·测试设计方法-因果图
详解金属互连中介质层

互连中的信号畸变(信号完整性揭秘)

当系统闹脾气:用「因果推断」哄稳技术的心
科普,三分钟了解NTP网络时间服务器

Node-RED初学者教程-三分钟学习



ChatGPT是一个好的因果推理器吗?





 三分钟了解PCB互连中因果和非因果响应
三分钟了解PCB互连中因果和非因果响应












评论