本文通过案例介绍了正态分布和贝塔分布的概念。
正态分布
正态分布,是一种非常常见的连续概率分布,其也叫做常态分布(normal distribution),或者根据其前期的研究贡献者之一高斯的名字来称呼,高斯分布(Gaussian distribution)。正态分布是自然科学与行为科学中的定量现象的一个方便模型。
各种各样的心理学测试结果和物理现象的观测值,比如光子计数等都被发现近似地服从正态分布。甚至生活中很多现象的表征结果也符合正态分布的分布规律。尽管这些现象的根本原因经常是未知的,甚至被采样的样本的原始群体分布并不服从正态分布,但这个变量的采样分布均值仍会近似服从正态分布。
正态分布的概率密度函数呈左右对称的钟形,其具体表达式为:
![]()
因为正态分布是如此的常见而这个式子是如此的奇怪,我们打算重温高斯当年的推导过程,但部分细节不会那么严谨的证明,只是带领大家看看高斯当年的思路是如何的。
首先,高斯事先假定了如下条件,才得到了正态分布的连续密度函数。
即: 误差分布导出的极大似然估计 = 算术平均值
这里我们把全部过程用直白的语言复述一遍。


贝塔分布
贝塔分布,beta分布,简单来说,就是一个事件出现的概率的概率密度分布。
举个例子,篮球比赛的三分命中率是衡量篮球后卫运动员很重要的一个指标。通过过去的历史经验,我们知道运动员的三分命中率很难超过40%。假如老张是一个优秀老练的篮球后卫,其过去历史的三分命中率是35%,总投数为10000次,命中次为3500次。请问他在新赛季刚开始的时候,得到了一次三分投球机会,请问他这次投中的概率服从什么分布呢?
我们必须清楚,这个概率一定不是确定的,而是服从某种分布。这个概率密度分布函数应该在0.35处最大,沿两边逐渐递减。
这个概率就服从beta分布。确切的说,是服从
还有个运动员小张,而小张很年轻也很优秀,他的历史三分命中率也是35%,但是总投数为1000次,命中次数为350次。请问他在新赛季首投三分,命中概率的分布和老张一样吗?
明显不一样!虽然他们的历史投球命中率都是35%,但是我们直觉认为老张比小张更靠谱,老张首投命中的概率密度分布应该在0.35附近高于小张的。事实上,我们可以迅速借助python的scipy库中内置的beta统计方法。

我们来看一下图像。

的确如此。那么beta分布的具体表达式是什么呢?

关于伽马函数和贝塔函数,这里我们不做赘述。
需要指出的是,看起来beta分布的概率密度函数和高斯分布的曲线很像,实则不然。
再举个例子,假如老张的孙子也想做做运动员,老张煞有介事的统计了小小张的历史三分投数,为5投1中。问他下一次投球,也就是第六次投球,命中的概率的分布是怎样的?如果过去是5投2中,5投3中,和5投4中呢?

可以看到,beta分布的PDF和高斯分布的曲线形状差别可大了。
编辑:hfy
-
函数
+关注
关注
3文章
4352浏览量
63250 -
高斯分布
+关注
关注
0文章
6浏览量
2778
发布评论请先 登录
相关推荐
薄膜压力分布测量系统鞋垫式足底压力分布测试

薄膜压力分布测量系统轮胎胎纹压力分布测试

分布式云化数据库有哪些类型
基于ptp的分布式系统设计
6419,6419A光纤应变分布测试仪
图像高斯滤波的原理及FPGA实现思路

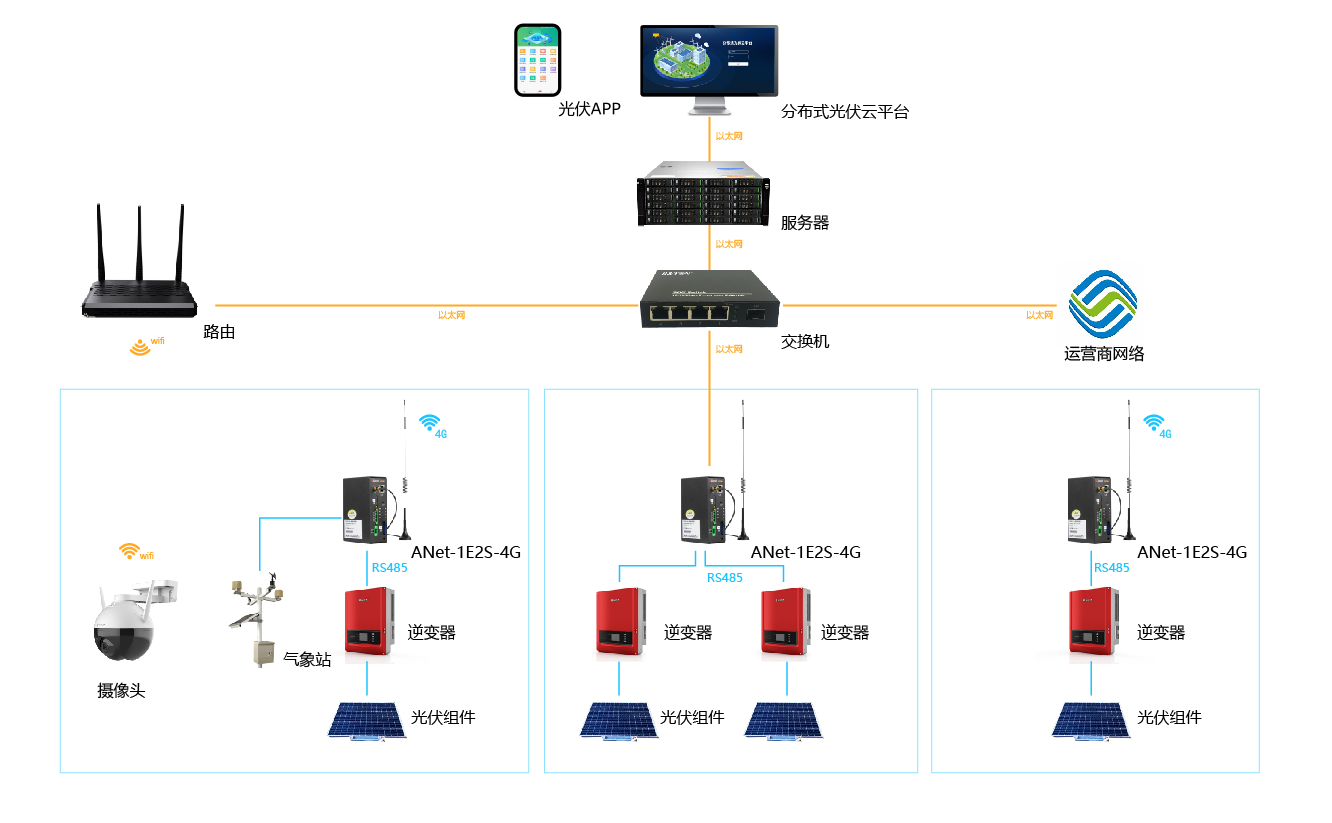
分布式光伏为企业带来哪些便捷!
分布式通信的原理和实现高效分布式通信背后的技术NVLink的演进
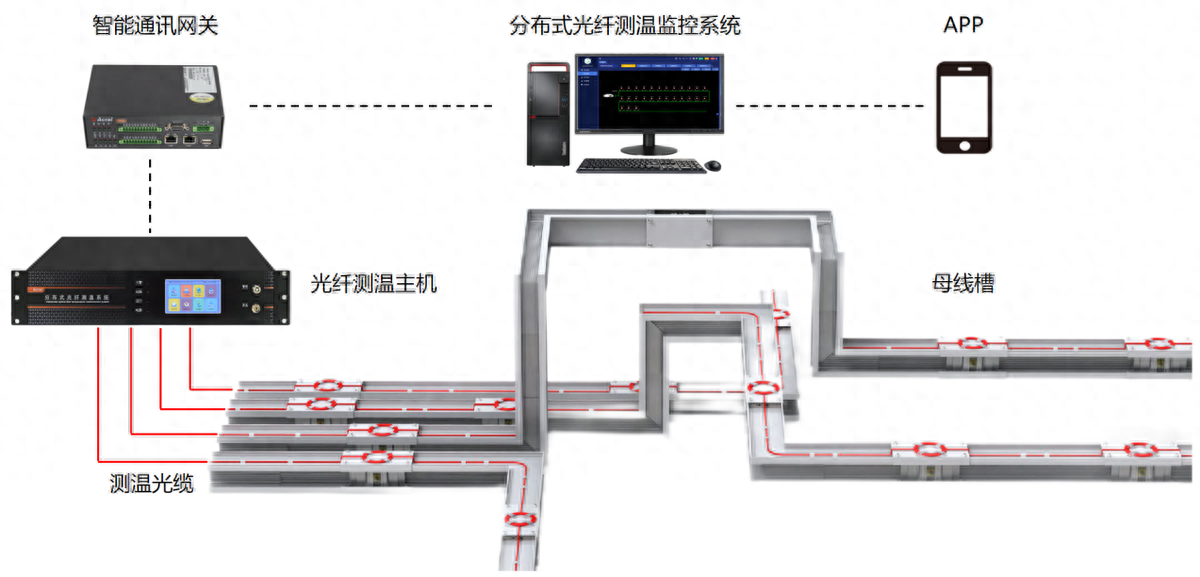
分布式光纤测温是什么?应用领域是?
雨刮器压力分布检测wipe有用吗?
安科瑞分布式光伏系统在某重工企业18MW分布式光伏中应用




 关于正态分布和贝塔分布的案例介绍
关于正态分布和贝塔分布的案例介绍











评论