树的递归结构
从一张图中解释什么是树
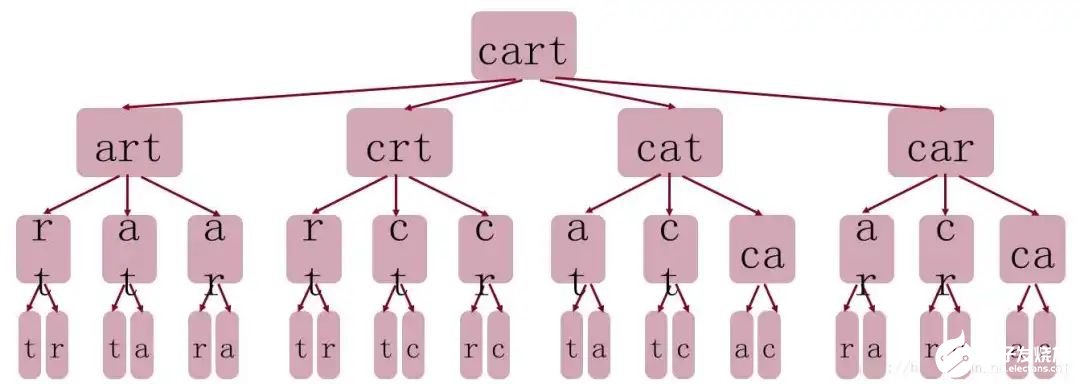
这张图,主要讲解关于cart这个单词的所有的可能组合,按照常理,需要先考虑三个字母的排列,然后对三个字母进行拆分,直到最后一个节点,这个过程就类似于树 到底什么是树
什么是树
树是节点集合(A tree is a collection of nodes),
集合:集合是允许一个元素都没有的集合,称之为空集。
首先,集合是允许一个元素都没有的集合,称之为空集,那么书是不是也允许一个节点都没有的呢,是的,一个节点都没有的树,称之为空树,如果不是空的,则会存在根节点r和零个或更多非空子树,T1,T2.。。Tk,他们的根由来自r的有向连接,什么叫有向边,大致可以理解为箭头。用图的关系说明树的内部关系
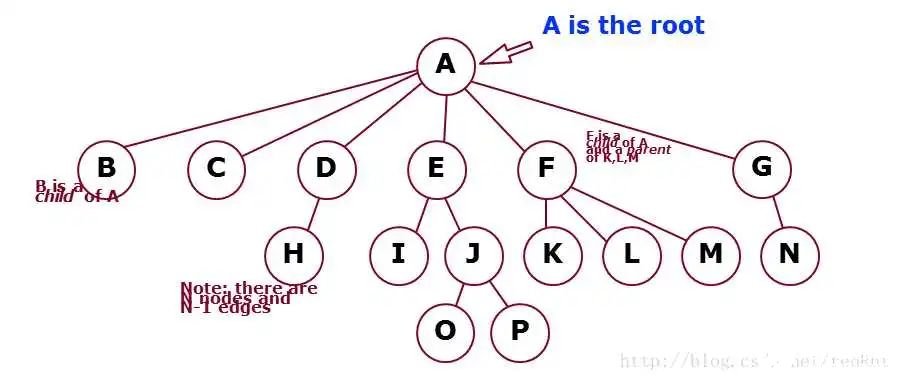
根节点(root)一棵树只有一个跟节点,所有的节点都在该节点的下面,尝试把图倒过来看,可以看成一个我们日常见到的数的根部,在这里显然字母A就是这颗树的根节点。
子节点,父节点,一个节点,它对应的下面有连这的节点,那么被连着的节点就是这个节点的子节点,也叫做孩子,那么这个节点叫做被连接的节点的父亲,看图,B被A连这,所以B是A的一个孩子,同理,CDE等等这一行都是A的孩子,同时F,它连这K L M 同时被A连这,那么F是A的一个孩子,同时又是K L M 的父亲。
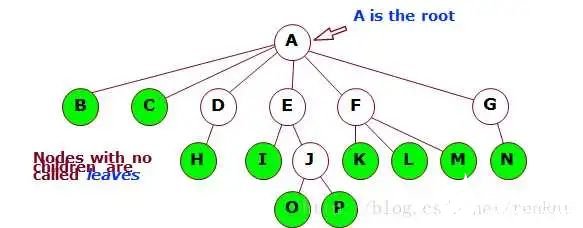
树叶:树叶就是那些没有孩子的节点,比如B,C,D等等,例如下图的绿色部分。
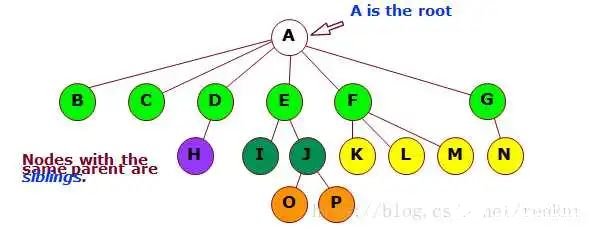
兄弟: 按照我们的理解,同一个父母生的当然是兄妹,如下图所示,颜色相同的都是兄妹
路径 我们同样可以定义从父亲到他孩子的路径,下面的路径,我们就取上图的一部分,一个子树,作为例子
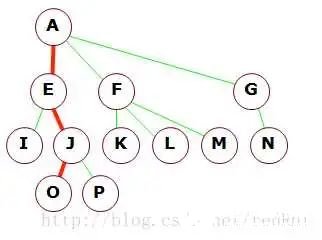
比如,A->O的路径为A->E->J->O它的长度为3,实际为它的边数,图中红色的部分。
节点的深度:节点的深度指的是节点到树根的长度,看下图,我们可以轻易的知道,j节点的深度为2,可以理解为 A-> E -> J 边长为2.显然,此时根节点的深度为0.
节点的高度:高度是从节点到叶子的最长路径,比如节点F的高度为1,显然所有叶子节点高度为0.
树的高度,树的高度是跟的高度,显然在这图中,树的高度为3,A->O
树的特点
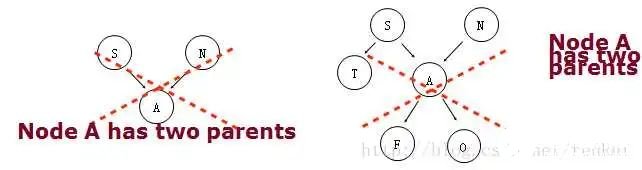
按照正常的逻辑,一个人不能同时有两个父亲,所以树也一样,下图的两个就解释了这个问题
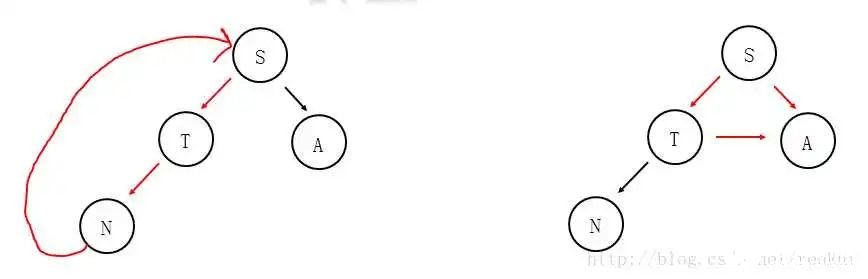
一颗正常的树,它的树枝是不会长成一个圆的,所以,树中,是不可能出现环形的。图中,红色箭头构成了一个环,所以都不是一颗树。
树的存储结构
树的存储结构有三种,分别为,双亲表示法,孩子表示法,孩子兄弟表示法。
双亲表示法
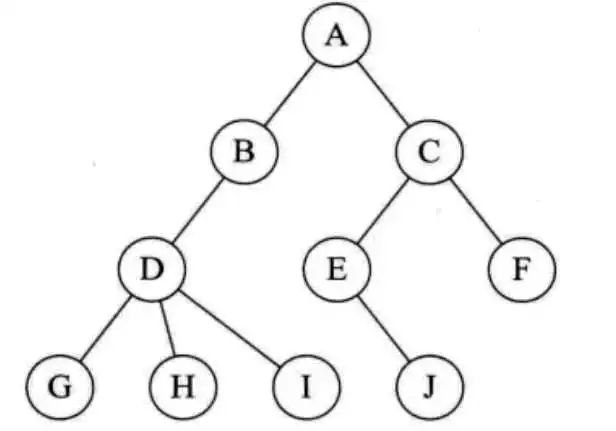
假设一组连续空间保存着树的特点,同时在每个节点中,附带一个指示器表示双亲节点中链表的为位置,也就是说,每个节点除了知道自己是谁以外,还知道他的双亲在哪里。
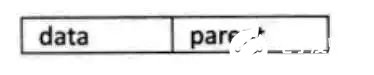
其中data是数据域,存储结点的数据信息。而parent是指针域,存储该结点的双亲在数组中的下标。
//树的双亲表示法结点结构定义 #define MAX_TRUE_SIZE 100 typedef int TElemType //树结点的数据类型 //结点结构 typedef struct PTNode { TElemType data; //结点数据 int parent; //双亲位置 }PTNode //树结构 typedef struct { PTNode nodes[MAX_TRUE_SIZE]; //结点数组 int r,n //根的位置和结点数 }PTree
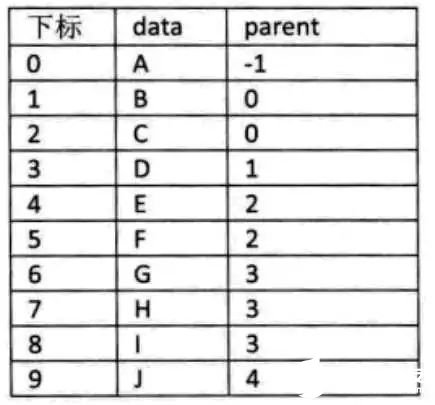
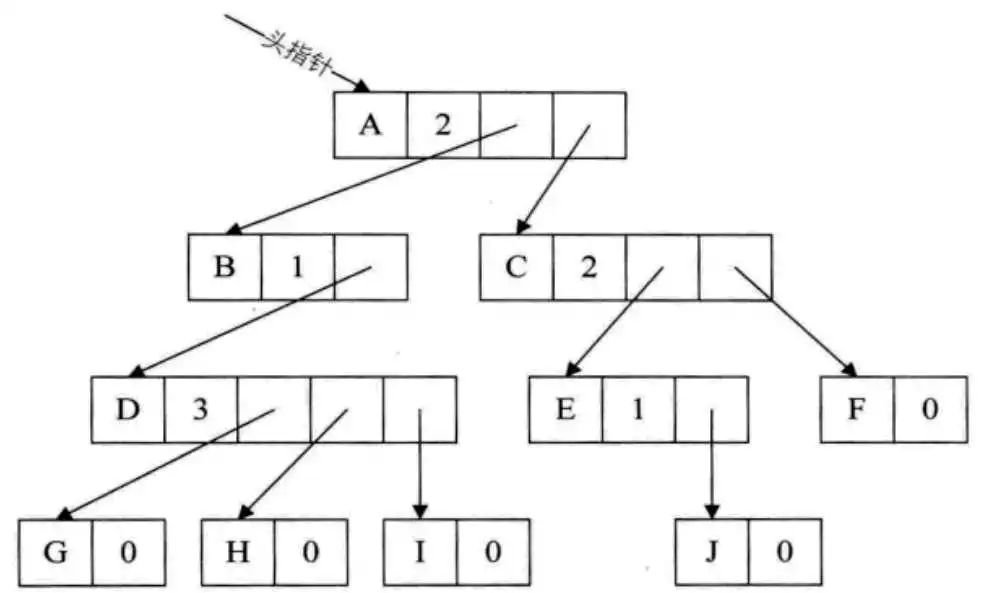
有了这样的数据结构就可以来实现双亲表示法。由于根结点是没有双亲的,所以我们约定根结点的位置域设置为-1,这也就意味着,我们所有的结点都存有他双亲的位置。如图1-2中的树结构和表1-3中的树双亲表示。
这样的存储结构,我们可以根据结点的parent’指针很容易找到他的双亲结点,时间复杂度为O(1),直到parent为-1时,表示找到了树结点的根
孩子表示法
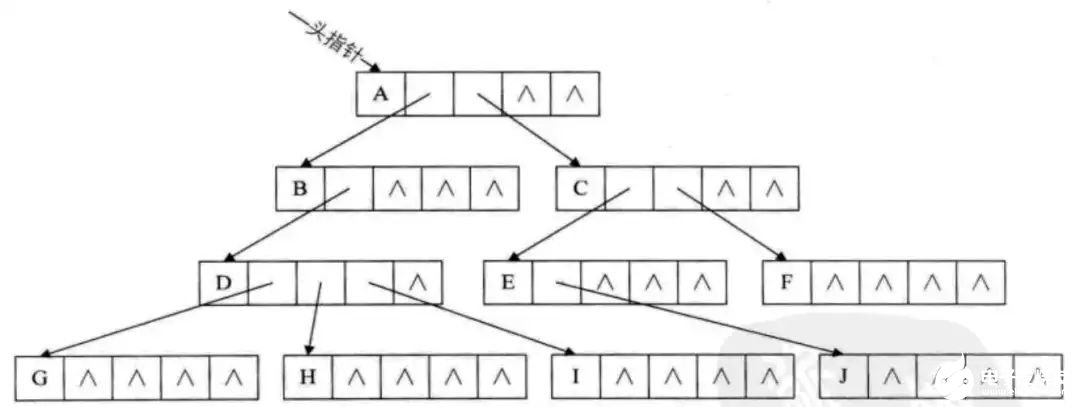
换一种完全不同的考虑方法,由于树中每个结点可能有多棵子树,可以考虑用多重链表。每个结点有多个指针域,其中每个指针指向一颗子树的根结点,我们把这种方法叫做多重链表的表示方法。不过,树的每个结点的度,也就是他的孩子个数是不同的,所以设计两种方法:
方案一
指针域的个数就等于树的度,树的度就是树各个结点度的最大值。其结构如图

其中data是数据域,child1到childd是指针域,用来指向该结点的孩子结点。对于图1-1来说,树的度是3,所以我们指针域个数就是3,
方案二
每个结点指针域的个数等于该结点的度,我们专门取一个位置来存储结点指针的个数。

data为指针域,degree为度域,也就是存储该结点的孩子结点的个数
这就是我们要说的孩子表示法,把每个结点的孩子都排列起来,以单链表为存储结构,则n个结点有n个孩子链表,如果是叶子结点则此单链表为空。然后n个头指针又组成一个线性表,采用顺序存储结构,存放进一个一维数组,
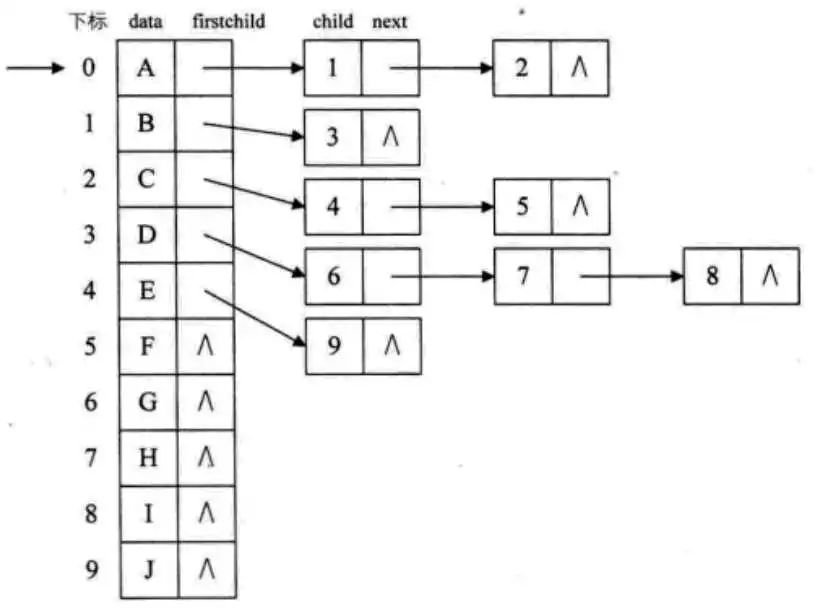
为此,设计两种存储结构,一个是孩子链表的孩子结点,

child是数据域,用来存储某个结点在表头数组中的下标。next是指针域,用来存储指向结点的下一个孩子结点的指针。另一个是表头数组的表头结点。

data是数据域,存储某结点的数据信息,firstchild是头指针域,存储该结点的孩子链表的头指针。
//树的孩子表示法结构定义
#define MAX_TRUE_SIZE 100
typedef struct CTNode //孩子结点
{
int child;
struct CTNode *next;
}*ChildPtr;
//表头结构
typedef struct
{
TElemType data;
ChildPtr firstchild;
}CTBox;
//树结构
typedef struct
{
CTBox nodes[MAX_TRUE_SIZE]; //结点数组
int r,n; //根的位置和结点数
}CTree
把把双亲表示法和孩子表示法综合一下表示如下
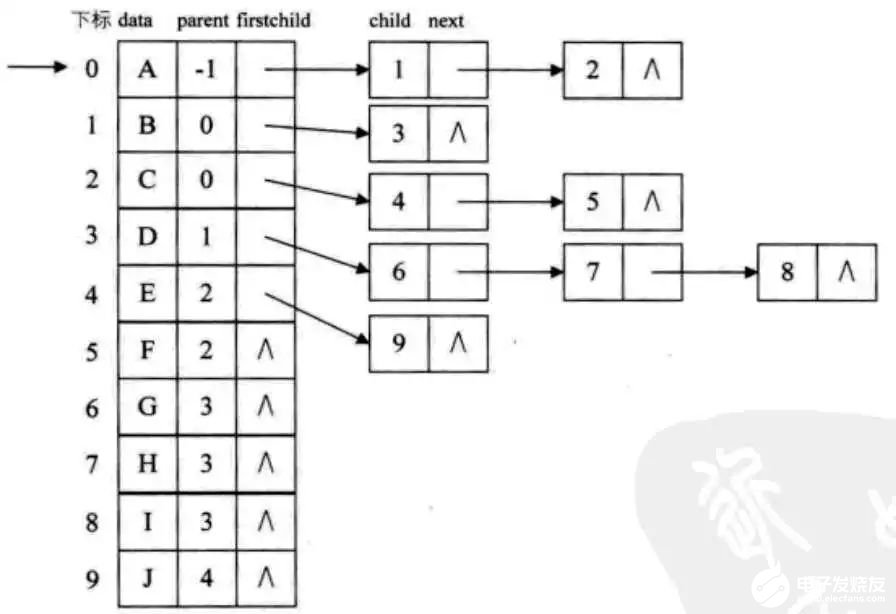
这种表示法叫做双亲孩子表示法,应该算是孩子表示法的改进。
孩子兄弟表示法
任一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。因此。我们设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟。

data是数据域,fitstchild为指针域,存储该结点的第一个孩子结点的存储地址,rightsib是指针域,存储该结点的右兄弟结点的存储位置。
//孩子兄弟表示法结构定义
typedef struct CSDNode
{
TElemType data;
struct CSNode *firstchild,*rightsib;
}CSNode,*CSTree;
这种方法的示意图如下所示
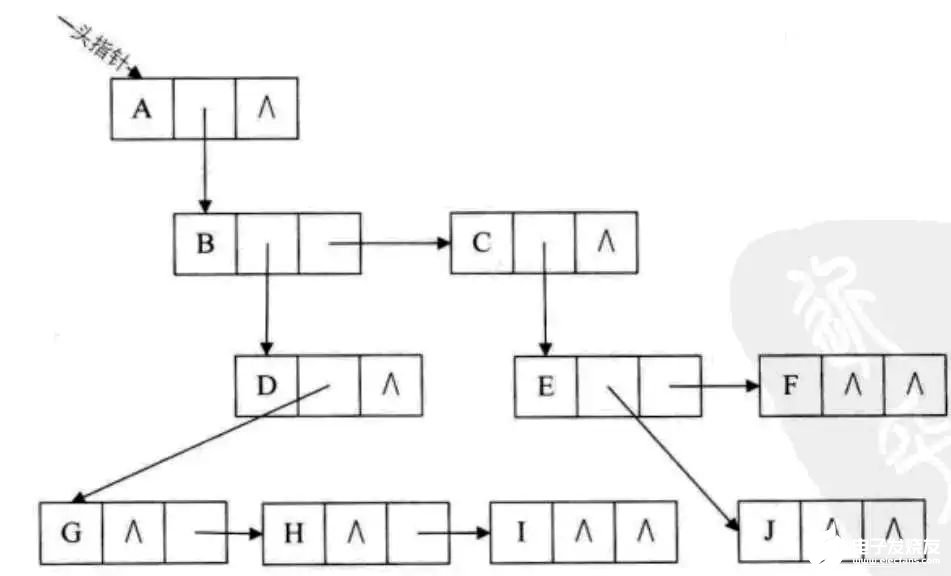
这种表示法,给查找某个结点的某个孩子带来了方便,只需要通过firstchild找到此结点的长子,然后在通过长子结点的rightsib找到它的二弟,接着一直找下去,直到找到具体的孩子。
编辑:hfy
-
数据结构
+关注
关注
3文章
573浏览量
40124 -
存储结构
+关注
关注
0文章
21浏览量
9713
发布评论请先 登录
相关推荐
什么是默克尔树(Merkle Tree)?如何计算默克尔根?
铁电存储器的结构特点
存储器的层次结构包括哪些
递归神经网络和循环神经网络的模型结构
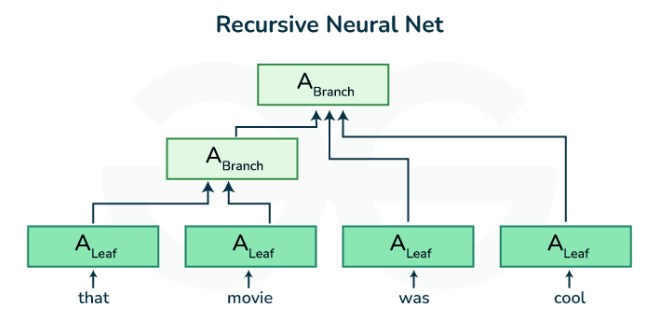
递归神经网络的实现方法
递归神经网络结构形式主要分为
递归神经网络与循环神经网络一样吗
递归神经网络的结构、特点、优缺点及适用场景
原理图设计里两颗重要的树(国产EDA)
高频高速覆铜板结构构成
什么是计算机网络的拓扑结构?主要的拓扑结构有哪些?
网络拓扑结构有几种?各有什么优缺点?
MCP251X can驱动移植nuc980采样用设备树配置时,中断如何配置设备树?
半导体芯片结构分析
用于室内植物或圣诞树的 Raspberry Pi Pico 水监控器




 树的递归结构和树的存储结构分析
树的递归结构和树的存储结构分析










评论