模数转换器(ADC)中的采样现象引发了混叠和电容反冲问题,为了解决这些问题,设计人员使用了滤波器和驱动放大器,这带来了自己的挑战。这使得在中带宽应用领域实现精确的直流和交流性能成为一个挑战,设计人员最终为此付出了折衷的系统目标。
ADC通过简化信号链来固有地并显着地解决采样问题。它们消除了对抗混叠滤波器和缓冲器的需求,并解决了信号链偏移误差和与其他组件相关的漂移问题。这些好处可缩小解决方案的规模,简化解决方案设计,并改善系统的相位匹配和整体延迟。
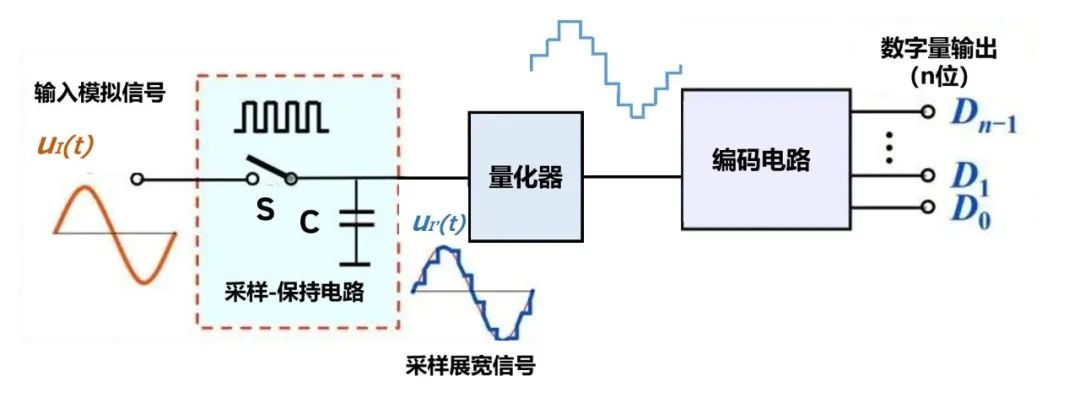
数据的数字化涉及采样和量化的两个基本过程,如图1所示。采样是第一步,其中使用采样将连续时间变化的模拟信号x(t)转换为离散时间信号x(n)。频率fS。结果平均间隔为1 / TS(fS = 1 / TS)。
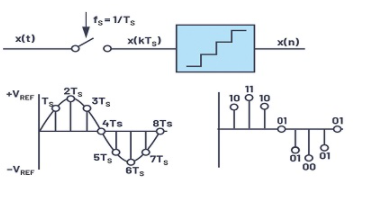
图1.数据采样
第二步是量化,将这些离散时间样本的值近似为有限的可能值之一,并用数字代码表示,如图1所示。量化为一组有限的值会导致数字化错误,称为量化噪声。
采样过程还会导致混叠,在混叠中,我们会看到输入信号的折返及其在采样和保持时钟频率附近的谐波。奈奎斯特准则要求采样频率至少是信号中包含的最高频率的两倍。如果采样频率小于最大模拟信号频率的两倍,则将发生称为混叠的现象。
为了理解混叠在时域和频域中的含义,首先考虑如图2所示采样的单音正弦波的时域表示形式。在此示例中,采样频率fS不至少2fa,但仅略高于模拟输入频率fa,因此无法满足奈奎斯特标准。请注意,实际样本的模式会在等于fS – fa的较低频率下产生混叠正弦波。
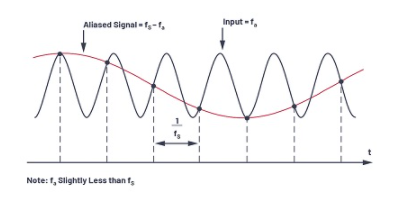
图2.混叠:时域表示。
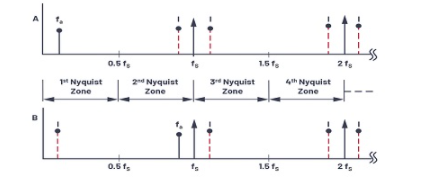
图3.混叠:在频域中的表示。
这种情况的相应频域表示如图3所示。
奈奎斯特带宽定义为从直流到fS / 2的频谱。频谱被划分为无数个奈奎斯特区,每个区的宽度等于0.5fS。实际上,理想的采样器由ADC和FFT处理器代替。FFT处理器仅提供从直流到fS / 2的输出;也就是说,出现在第一个奈奎斯特区域中的信号或别名。
考虑由理想脉冲采样器在频率fS采样的频率为fa的单频正弦波的情况(见图1)。还假设fS》 2fa。采样器的频域输出在fS的每一个倍数附近显示原始信号的别名或图像。也就是说,在等于|的频率下 ±KfS±fa |,K = 1、2、3、4,依此类推。
现在考虑信号在图3中第一个Nyquist区域之外的情况。信号频率仅略小于采样频率,这与图2时域表示中所示的条件相对应。请注意,即使信号在第一个奈奎斯特区域之外,其图像(或别名)fS – fa落在内部。返回图3,很明显,如果一个不想要的信号出现在fa的任何镜像频率上,它也会出现在fa上,从而在第一奈奎斯特区中产生一个杂散频率分量。
应对精度性能挑战
对于高性能应用,系统设计人员需要解决量化噪声,混叠和采样过程中产生的开关电容器输入采样问题。两种类型的精密ADC(即工业上可用的逐次逼近寄存器(SAR)和sigma-delta ADC)都是使用基于开关电容器的采样技术设计的。
量化噪声
在理想的Nyquist ADC中,ADC的LSB大小将确定在进行模数转换时添加到输入的量化噪声。该量化噪声分布在fS / 2的带宽上。为了对抗量化噪声,第一种技术是过采样,即以比奈奎斯特频率高得多的速率采样输入信号,以提高信噪比(SNR)和分辨率(ENOB)。在过采样中,采样频率选择为Nyquist频率(2×fIN)的N倍,结果,现在相同的量化噪声必须在N倍Nyquist频率上扩展。这也放宽了对抗混叠滤波器的要求。过采样率(OSR)定义为fS / 2fIN,其中fIN是感兴趣的信号BW。作为一般准则,对ADC进行四倍的过采样可提供额外的分辨率,或动态范围增加6 dB。增加过采样率将导致整体噪声降低,并且由于过采样而导致的动态范围(DR)改善为ΔDR= 10log10 OSR,以dB为单位。
过采样在本质上与集成的数字滤波器和抽取功能一起使用和实现。Σ-ΔADC中的基本过采样调制器对量化噪声进行整形,以使其大部分出现在目标带宽之外,从而导致低频处的整体动态范围增加,如图4所示。数字低通滤波器(LPF) )然后去除感兴趣带宽之外的量化噪声,抽取器将输出数据速率降低回奈奎斯特速率。
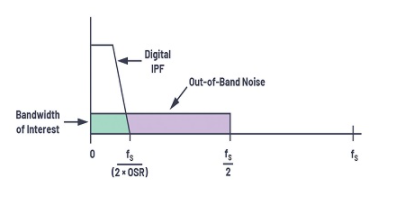
图4.过采样示例。
噪声整形是另一种减少量化噪声的技术。在sigma-delta ADC中,在环路滤波器之后的环路内使用低分辨率量化器(一位到五位)。DAC用作反馈,从输入中减去量化信号,如图5所示。
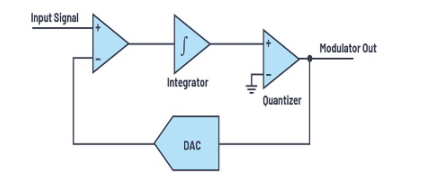
图5.噪声整形。
积分器将不断总结量化误差,从而将量化噪声整形为更高的频率,然后可以使用数字滤波器对其进行滤波。图6说明了典型sigma-delta ADC输出x [n]的功率谱密度(PSD)。噪声整形斜率取决于环路滤波器H(z)的阶数(见图11),为(20×n)dB /十倍频程,其中n是环路滤波器的阶数。通过将噪声整形和过采样相结合,sigma-delta ADC可实现高分辨率带内。带内带宽等于fODR / 2(ODR代表输出数据速率)。通过增加环路滤波器的阶数或通过增加过采样率可以获得更高的分辨率。
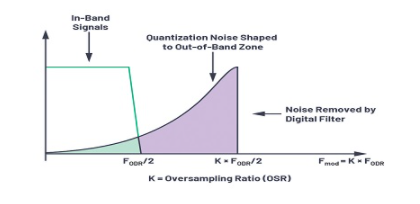
图6.过采样和噪声整形图。
混叠
为了在高性能应用中消除混叠,使用了更高阶的抗混叠滤波器来避免任何数量的折返。抗混叠滤波器是一种低通滤波器,其带宽限制了输入信号,并确保信号中没有超出可以折返的目标带宽的频率分量。滤波器的性能将取决于带外信号与fS / 2的接近程度以及所需的衰减量。
对于SAR ADC,输入信号带宽和采样频率之间的差距并不大,因此我们需要一个更高阶的滤波器,这需要具有更高功率和更大失真的复杂,更高阶滤波器设计。例如,如果200 kSPS采样速度SAR的输入带宽为100 kHz,则抗混叠滤波器将需要拒绝大于100 kHz的输入信号,以确保没有混叠。这需要非常高阶的滤波器。图7显示了陡峭的曲线需求。

图7.别名要求。
如果选择400 kSPS的采样速度来放宽滤波器的阶数,则对于》 300 kHz的输入频率,则需要抑制。增加采样速度将增加功率,对于双倍速度,功率也将增加一倍。由于采样频率远高于输入带宽,因此,以功率为代价的进一步过采样将进一步放宽抗混叠滤波器的要求。
在sigma-delta ADC中,输入以更高的OSR进行过采样,因此抗混叠滤波器的要求有所放宽,因为采样频率远高于输入带宽,如图8所示。
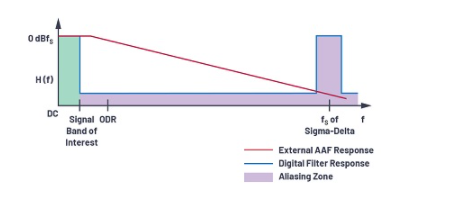
图8. sigma-delta中的抗混叠滤波器要求。
图9给出了SAR和离散时间sigma-delta(DTSD)架构的AAF复杂度的想法。如果我们采用100 kHz的–3 dB输入带宽以在采样频率fS处实现102 dB衰减,则DTSD ADC将需要二阶抗混叠滤波器,而在fS处获得相同的衰减将需要使用SAR ADC。
对于连续时间sigma-delta(CTSD)ADC,衰减是固有的,因此我们不需要任何抗混叠滤波器。
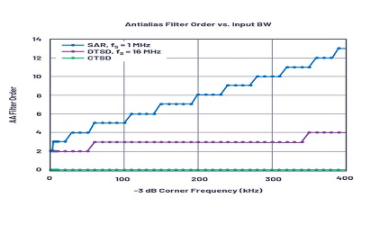
图9.各种架构的AAF过滤器要求。
这些滤波器可能是系统设计人员的痛点,他们必须针对它们在目标频段内提供的下垂进行优化,并提供尽可能多的抑制。它们还会给系统增加许多其他误差,例如失调,增益,相位误差和噪声,从而降低其性能。
而且,高性能ADC本质上是差分的,因此我们需要两倍数量的无源元件。为了在多通道应用中获得更好的相位匹配,信号链中的所有组件都必须匹配良好。结果,需要公差更严格的组件。
开关电容输入
开关电容器输入采样取决于采样输入到电容器上的建立时间,这会在采样开关打开/关闭时产生对充电/放电瞬态电流的需求。这被称为输入上的反冲,并且需要能够支持这些瞬态电流的输入驱动放大器。同样,要求在采样时间结束时稳定输入,并且采样输入的精度决定ADC的性能,这意味着驱动放大器需要在反冲事件之后迅速稳定下来。这导致需要一种高带宽驱动器,该驱动器应支持快速建立并吸收开关电容器工作的反冲。在开关电容输入中,每当采样打开时,驱动器就必须立即为保持电容提供电荷。如果驱动器具有足够的带宽功能,则只能及时提供电流的突然激增。由于开关的寄生效应,采样时会在驱动器上产生反冲。如果反冲在下一次采样之前没有稳定下来,将导致采样错误,从而破坏ADC输入。
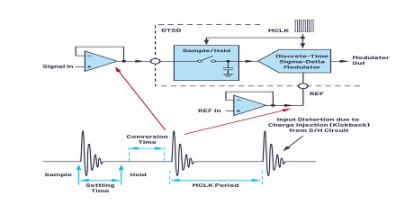
图10.采样反冲。
图10显示了DTSD ADC的反冲。例如,如果采样频率为24 MHz,则数据信号需要稳定在41 ns之内。由于基准也是开关电容输入,因此基准输入引脚上也需要高带宽缓冲器。这些输入信号和参考缓冲器会增加噪声并降低信号链的整体性能。此外,来自输入信号驱动器的失真分量(在S&H频率附近)进一步增加了抗混叠要求。同样,对于开关电容输入,采样速度的变化将导致输入电流变化。这可能会导致系统重新调整,以减少驱动ADC时驱动器或前一级产生的增益误差。
连续时间Sigma-Delta ADC
CTSD ADC是一种可替代的sigma-delta ADC架构,它利用了过采样和噪声整形等原理,但是具有实现采样操作的另一种方式,可带来明显的系统优势。
图11显示了DTSD架构和CTSD架构的比较。正如我们在DTSD架构中看到的那样,在循环之前对输入进行采样。环路滤波器H(z)在时间上是离散的,并使用开关电容积分器实现。反馈DAC也是基于开关电容的。由于输入端有采样,这将导致f S的混叠问题,因此在采样之前,需要在输入上附加一个抗混叠滤波器。
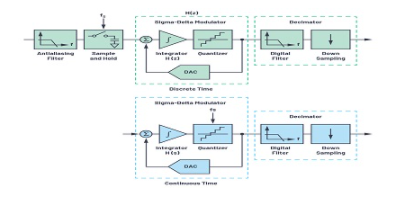
图11.离散时间和连续时间模块化框图。
CTSD在输入处没有采样器。而是在循环内部的量化器处对其进行采样。环路滤波器现在使用连续时间积分器是连续时间的,反馈DAC也是如此。与成形的量化相似,由于采样引起的混叠也成形。这样就产生了几乎不采样的ADC,从而形成了自己的一类。
与DTSD不同,CTSD的采样频率是固定的,而DTSD可以很容易地调整调制器的采样频率。同样,与开关电容器等效物相比,CTSD ADC对抖动的容忍度更低。现成的晶体或CMOS振荡器为本地ADC提供低抖动时钟,从而有助于避免在隔离状态下传输低抖动时钟并降低EMC。
CTSD的两个主要优点是固有的混叠抑制以及信号和参考的电阻输入。
固有的抗锯齿
在循环内移动量化器会导致固有的混叠抑制。如图12所示,输入信号在被采样之前先经过环路滤波器,而在量化器处引入的折返(混叠)误差也可以看到该滤波器。信号和混叠误差将具有与sigma-delta环路相同的噪声传递函数,并且在sigma-delta架构中将具有与量化噪声相似的噪声整形。因此,CTSD环路的频率响应自然会拒绝采样频率整数倍附近的输入信号,用作抗混叠滤波器。
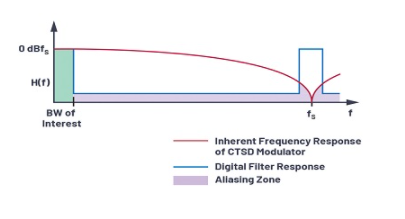
图12. CTSD调制器的频率响应。
电阻输入
与采样保持配置相比,在信号输入和参考输入上具有电阻输入使驱动更加容易。使用恒定的电阻输入,不会产生反冲,并且可以完全卸下驱动器。输入无失真,如图13所示。由于输入电阻恒定,因此消除了因增益误差而对系统进行的重新调谐。
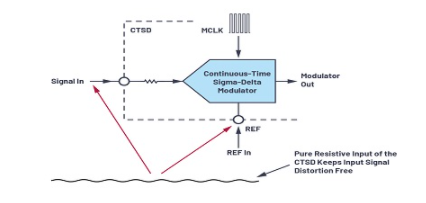
图13. CTSD的输入设置。
即使ADC具有单极性电源,模拟输入也可以是双极性的。这样可以消除从双极性前端到ADC的电平转换的需要。ADC的直流性能可能与输入电阻现在具有与输入共模相关的电流以及输入电流不同。
参考负载也是电阻性的,可以减少开关反冲,因此不需要单独的参考缓冲器。低通滤波器的电阻器可以在片上制成,以便可以与片上电阻性负载一起跟踪(因为它们可能是相同的材料),以减少增益误差温度漂移。
CTSD体系结构并不是新事物,但是工业和仪器市场的大趋势要求在更高带宽下具有直流和交流精度性能。此外,客户更喜欢能够满足大多数解决方案的单一平台设计,从而缩短了产品上市时间。
由于具有优于其他类型ADC的众多优势,CTSD架构已成为从高性能音频到蜂窝手机RF前端的广泛应用中的选择。好处包括更高的集成性和更低的功耗,但也可能而且更重要的是,因为使用CTSD解决了许多重要的系统级问题。由于许多技术缺陷,CTSD的使用以前仅限于相对音频频率/带宽和较低的动态范围。因此,高性能奈奎斯特速率转换器(如逐次逼近型ADC和过采样DTSD转换器)已成为用于高精度,高性能/中带宽应用的主流解决方案。
但是,最近的技术突破已经克服了许多限制。例如,AD7134 ADI公司支持基于CTSD的高精度DC至400 kHz带宽ADC,该ADC达到了更高的性能规格,同时提供了DC精度,从而为高性能仪器应用中的许多重要系统级问题提供了解决方案。AD7134还集成了异步采样率转换器(ASRC),该转换器以固定的CTSD采样速度得出的可变数据速率提供数据。输出数据速率可以独立于调制器采样频率,并且可以成功地将CTSD ADC用于不同的颗粒吞吐量。在粒度级别上灵活更改输出数据速率的灵活性还使用户能够使用相干采样。
固有的别名拒绝功能消除了对抗混叠滤波器的需求,从而减少了组件,并减小了解决方案的尺寸。更重要的是,不再出现抗混叠滤波器带来的性能问题,例如下垂,诸如偏移,增益和相位误差之类的误差以及系统中的噪声。抗混叠滤波器还会根据所需的抑制显着增加信号链中的整体延迟。去除滤波器可完全消除该延迟,从而在嘈杂的数字控制环路应用中实现精确转换。
在系统级别没有抗混叠滤波器的情况下,可以大大改善多通道系统中的相位匹配。这在要求低通道间失配的应用中特别有用,例如振动监测,功率测量,数据采集模块和声纳。由于其固有的滤波作用,CTSD ADC在系统级以及IC本身内部也不受任何干扰。在DTSD ADC和SAR ADC中,必须格外小心,以使ADC采样时的干扰更少。而且,由于固有的滤波作用,将不受电源线干扰的影响。使用恒定电阻模拟输入和参考输入,也可以完全消除驱动器要求。同样,这可以解决性能问题,例如偏移,增益,
由于显着减少了设计元素的数量,因此实现精度性能的努力非常少。这样可以缩短设计时间,缩短客户产品上市时间,简化BOM管理并提高可靠性。卸下抗混叠滤波器,驱动器和参考缓冲器将大大减少系统板的面积。仪表放大器可用于直接驱动ADC。例如,对于AD7134,由于它是仅差分输入的ADC,因此它具有差分仪表放大器,例如LTC6373可以用作驱动程序。图14中的比较显示了基于离散时间的信号链和基于连续时间的信号链的信号链。与等效的基于离散时间的信号链相比,我们的实验表明节省了70%的面积,这使其成为高密度多通道应用的绝佳选择。
总而言之,这种方法可显着减小系统尺寸,简化信号链设计,使系统更坚固,并通过简单的设计就可缩短上市时间,而无需牺牲精密仪器应用所需的任何性能参数。
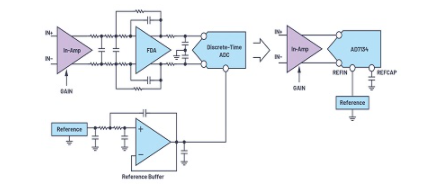
图14.基于离散时间(左)和基于连续时间(右)的信号链比较。

图15.离散时间和连续时间信号链的大小比较。
编辑:hfy
-
滤波器
+关注
关注
161文章
7808浏览量
178070 -
adc
+关注
关注
98文章
6498浏览量
544560 -
模数转换器
+关注
关注
26文章
3204浏览量
126828 -
驱动放大器
+关注
关注
0文章
45浏览量
16987 -
积分器
+关注
关注
4文章
100浏览量
28449
发布评论请先 登录
相关推荐
ADC122S706双通道同步采样模数转换器(ADC)数据表

ADS7844 8通道、12位采样模数转换器(ADC)数据表

ADS7841 4通道、12位采样模数转换器(ADC)数据表

ADC08DJ5200RF射频采样千兆采样模数转换器(ADC)数据表

ADC12DJ5200-EP射频采样千兆采样模数转换器(ADC)数据表

ADS7813低功耗、16位采样模数转换器(ADC)数据表

芯炽单通道14位ADC SC2245可作为光谱编码模数转换器
Σ-Δ模数转换器(ADC)技术一览

客户案例 | 多通道数模转换器ADC动静态参数测试解决方案




 模数转换器(ADC)的数据数字化采样和量化方案设计
模数转换器(ADC)的数据数字化采样和量化方案设计










评论