当我们在听一首歌时,我们把正弦波形看作音乐。它们的振幅告诉我们信号有多大,频率告诉我们声音是低音还是高音。然而,第三个重要参数,即相位,我们的耳朵是感觉不到的。本文将解释并给出更多关于相位参数的细节,因此,第一节将介绍相位和相位差的概念。在第二部分,我们详细介绍了相移概念的更多方面,并着重讨论了当信号不存在时的特定情况同步化了第三节和最后一节将最后介绍相位差在干涉现象中的重要作用。
演示
正弦信号的相位通常用Φ表示,并以弧度(rad)或度数(°)测量,可以在-π和+πrad或-180°和+180°之间变化。在图表中,交流信号的相位表示其相关正弦函数在时间原点的初始状态:
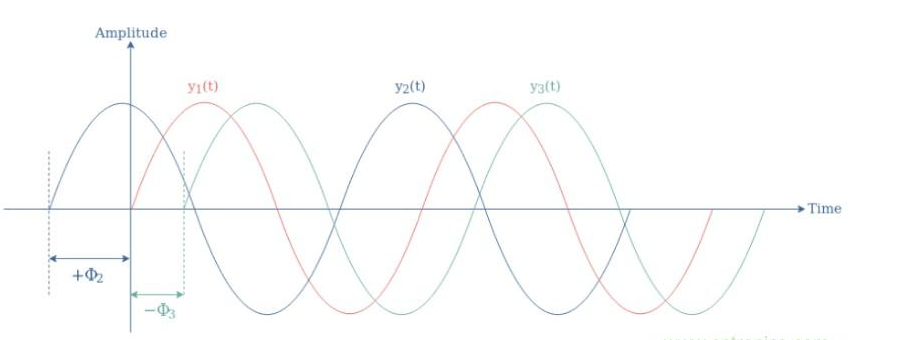
图1:具有不同相位的三个正弦波的图示
一个信号的相位Φ可以有三种不同的性质,它决定了波形绕纵轴的位置:
等于0(°或rad),例如用作参考信号的信号y1(t)
如信号y2(t)为正
如信号y3(t)为负
单个信号的相位不是很相关,因为无论交流波形是电的还是机械的,如果信号有相位,感知将保持不变。更重要的是,可以清楚地感知到的是相位差,也称为相同频率的两个信号之间的相移。
相位差
在相同频率的信号之间重要的是在这一节中我们只讨论两个频率相同的信号之间的相移。因此,考虑具有不同相位和可能不同振幅的两个相同频率的信号:y1(t)=Asin(ωt+Φ1)和y2(t)=Bsin(ωt+Φ2)。我们将相位差定义为ΔΦ21=Φ2-Φ1。在图1中,我们有ΔΦ21=+Φ2,ΔΦ31=-Φ3,以及ΔΦ32=-Φ3-Φ2。正相位差,如ΔΦ21,表明信号y2(t)暂时先于参考信号y1(t),我们也认为y2(t)超前于y1(t)。负相位差,如ΔΦ31和ΔΦ32,表明信号y3(t)跟随信号y1(t)和y2(t),我们也说y3(t)滞后于y1(t)和y2(t)。在相位差可以取的-180°和+180°或-π和+πrad之间的所有值中,可以突出显示几个,如下图2所示:
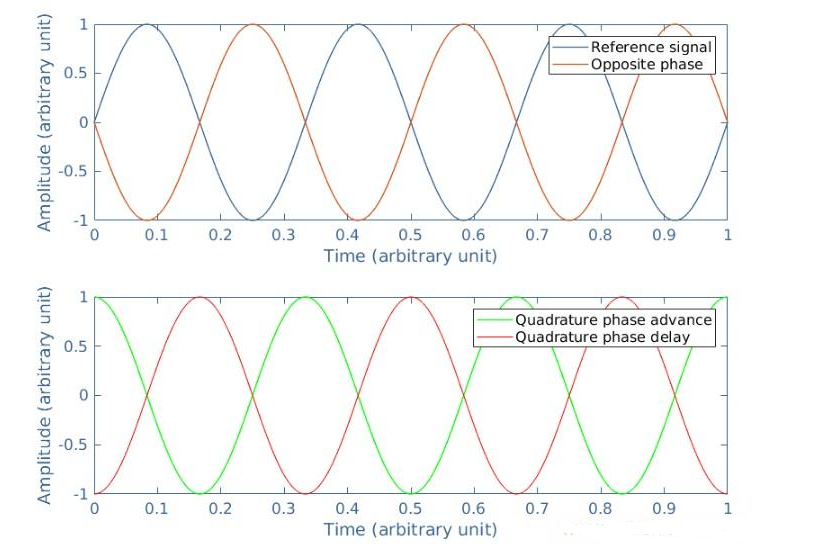
图2:一些相关相移的图示
相反相的特征是相移为+180°或+πrad,这与-180°或-πrad完全相同。如果参考信号为Vref=vrefsin(ωt),则相反的信号为Vopp=vrefsin(ωt+π)=-vrefsin(ωt),因此,Vref+Vopp=0。正交信号的特征是“前进”的相移为+90°或+π/2 rad,对于“延迟”,相移为-90°或-π/2 rad,我们特别关注电流(I)和电压(V)信号在电偶极子上的相移,并研究其影响电源。输入直流区,偶极子的耗散功率(P)由电压和电流的乘积给出:
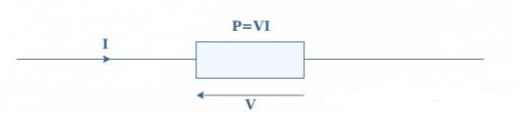
在交流系统中,这种表示不再是真实的,因为电压和电流都是交替的。考虑偶极子的电压为V=Vrms√2.sin(ωt),相同频率的电流呈现+ΔΦ:I=Irms√2.sin(ωt+Φ)。以Vrms和Irms为均方根值。它可以证明,交流区偶极子中耗散的有功功率由公式1给出:

公式1:交流状态下的耗散功率
cos(Φ)这个术语被称为功率因数,它给出了受体吸收电源功率的效率。这个因子是一个介于0和1之间的实数,这两个极值反映了截然不同的行为:如果cos(Φ)=1,偶极子被认为是纯电阻,电压和电流之间的相移为零。偶极子不存在任何感应或电容行为。如果cos(Φ)=0偶极子是纯无功的,电压和电流之间的相移最大,等于±90°或±π/2 rad。在这种情况下,偶极子不消耗任何功率,而是将其返回给电路。The方程式1中给出的功率称为有功功率(P),Vrms×Irms的乘积称为视在功率,并记下S。如果元件为纯电阻元件,则为消耗的功率。Vrms×Irms×sin(Φ)是无功功率,并注明Q。由于在同一复杂功率图中相移ΔΦ,这些量可以联系起来:
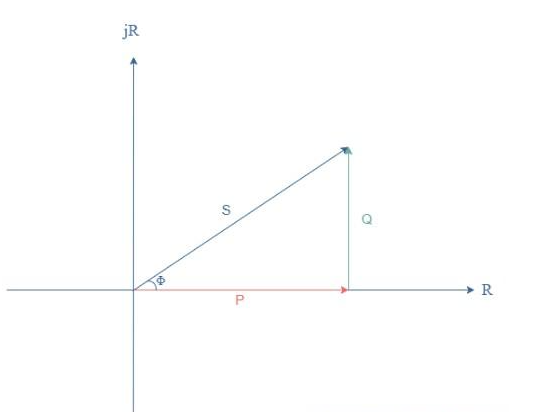
图3:有功、视在和无功功率的定义
在本节中,我们考虑两个频率相近但不完全相同的信号y1(t)和Φ的相移y2(t):ω1≠ω2。通常,只能为两个频率相同的信号定义相移,但在这种特殊情况下,由于频率相似,定义相位差仍然有意义。如果频率相差太大,通常当ω1>2ω2时,由于相位差和信号一样变化,因此定义它是没有意义的本身。在在信号频率相似的情况下,相位差不再是常数,而是随时间缓慢变化:ΔΦ(t)=(ω2-ω1)t+Φ。这两个信号的叠加很有趣,因为会产生拍频现象,如图4所示:
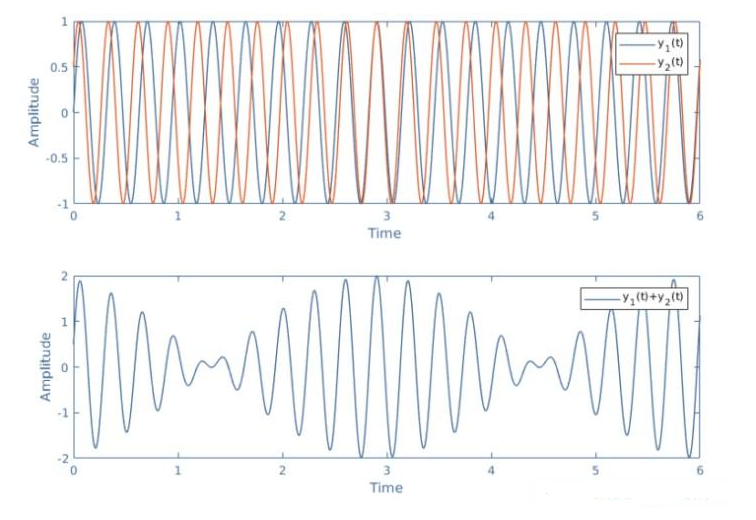
图4:两个频率相近信号之间跳动现象的图示
干扰
我们可以在图4中看到,正弦波形的叠加有时除了信号处于相位时的振幅之外,有时会导致相距,或者当信号与相位相反时进行减法。这种现象被称为干扰,当信号相同时发生频率。考虑同样频率的正弦波形又有两种:y1(t)=A1sin(ωt+Φ1)和y2(t)=A2sin(ωt+Φ2)。我们把y3(t)称为叠加y1(t)+y2(t)和A3的振幅。可以看出,y3(t)的振幅满足以下公式:
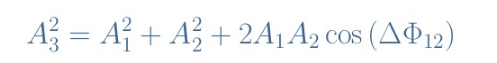
公式2:叠加信号的振幅
我们可以注意到y1(t)和y2(t)之间的相位差对最终的信号幅度起着重要的作用。有两种情况值得注意:ΔΦ12=0,信号同相,振幅A3最大,满足A32=(A1+A2)2。在这种情况下,我们认为y1和y2之间的干扰是建设性的,ΔΦ12=±πrad,信号相位相反,振幅A3最小,满足A32=(A1-A2)2。在这种情况下,y1和y2之间的干扰是破坏性的。什么时候相位差在这两个极值之间,我们可以绘制一个图表,显示A3随ΔΦ12的变化:
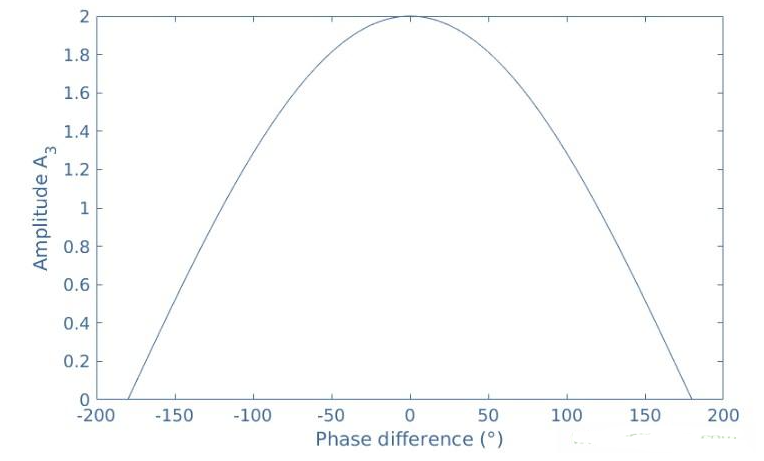
图5:作为相位差函数的结果信号的振幅
在这个图中,为了简单起见,我们选择A1=A2。我们又可以看到,当ΔΦ12=0,A3=A1+A2=2,当ΔΦ12=±180°时,A3=A1-A2=0。
结论
本教程详细介绍了相位和相位差的概念,并通过一些例子指出了相位和相位差的重要性示例。首先总之,我们给出了什么是信号的相位,以及用什么单位来测量。然而,仅仅是相位的概念并不十分相关,在第二节的第一段中,我们定义了相移ΔΦ,并给出了一些与相位差的特殊情况相关的词汇:同相(ΔΦ=0°),相位的对立(ΔΦ=±180°)和正交(ΔΦ=±90°)。在第二小节中,我们强调了电路中电流和电压之间相移的重要性。在任何电子元件中消耗的功率与相移的余弦成正比,称为功率系数。最后一节,我们将干涉现象与相移参数联系起来并加以解释。
编辑:hfy
-
电路设计
+关注
关注
6664文章
2426浏览量
203196 -
相位差
+关注
关注
1文章
31浏览量
15022
发布评论请先 登录
相关推荐
基于AD8302的单片宽频带相位差测量系统设计




 电路设计相位和相位差在干涉现象中的重要作用
电路设计相位和相位差在干涉现象中的重要作用











评论