二分查找算法如何运用？

读完本文，你可以去力扣解决：410.分割数组的最大值（Hard）

经常有读者问我，读了之前的爆文二分查找框架详解之后，二分查找的算法他写的很溜了，但仅仅局限于在数组中搜索元素，不知道底怎么在算法题里面运用二分查找技巧来优化效率。

那我先说结论，你想用二分查找技巧优化算法，首先要把 for 循环形式的暴力算法写出来，如果算法中存在如下形式的 for 循环：

//func(i)是i的单调函数（递增递减都可以） intfunc(inti); //形如这种for循环可以用二分查找技巧优化效率 for(inti=0;i< n; i++) {     if (func(i) == target)         return i; }

如果func(i)函数是在i上单调的函数，一定可以使用二分查找技巧优化 for 循环。

「在i上单调的函数」是指func(i)的返回值随着i的增加而增加，或者随着i的增加而减小。

为什么满足这个条件就可以使用二分查找？因为这个逻辑和「在有序数组中查找一个元素」是完全一样的呀！

在有序数组nums中查找某一个数target，是不是最简单二分查找形式？我们看下普通的 for 循环遍历算法：

//nums是一个有序数组 int[]nums; //target是要搜索的元素 inttarget; //搜索target在nums中的索引 for(inti=0;i< nums.length; i++) {     if (nums[i] == target)         return i; }

既然nums是有序数组，你把nums[i]看做函数调用，是不是可以理解为nums在参数i上是单调的？这是不是和之前说的func(i)函数完全一样？

当然，前文二分查找框架详解说过，二分查找算法还有搜索左侧、右侧边界的变体，怎么运用到具体算法问题中呢？

还是注意观察 for 循环形式，只是不一定是func(i) == target作为终止条件，可能是<=或者>=的关系，这个可以根据具体的题目意思来推断，我们实操一下力扣第 410 题「分割数组的最大值」，难度Hard：

函数签名如下：

intsplitArray(int[]nums,intm);

这个题目有点类似前文一道经典动态规划题目高楼扔鸡蛋，题目比较绕，又是最大值又是最小值的。

简单说，给你输入一个数组nums和数字m，你要把nums分割成m个子数组。

肯定有不止一种分割方法，每种分割方法都会把nums分成m个子数组，这m个子数组中肯定有一个和最大的子数组对吧。

我们想要找一个分割方法，该方法分割出的最大子数组和是所有方法中最大子数组和最小的。

请你的算法返回这个分割方法对应的最大子数组和。

我滴妈呀，这个题目看了就觉得 Hard，完全没思路，这题怎么能和二分查找算法扯上关系？

说个小插曲，快手面试有一道画师画画的算法题，很难，就是以这道题为原型。当时我没做过这道力扣题，面试有点懵，不过之前文章二分查找算法运用写了两道类似的比较简单的题目，外加面试官的提示，把那道题做出来了。

面试做算法题的时候，题目一般都会要求算法的时间复杂度，如果你发现 O(NlogN) 这样存在对数的复杂度，一般都要往二分查找的方向上靠，这也算是个小套路。

言归正传，如何解决这道数组分割的问题？

首先，一个拍脑袋的思路就是用回溯算法框架暴力穷举呗，我简单说下思路：

你不是要我把nums分割成m个子数组，然后计算巴拉巴拉又是最大又是最小的那个最值吗？那我把所有分割方案都穷举出来，那个最值肯定可以算出来对吧？

怎么穷举呢？把nums分割成m个子数组，相当于在len(nums)个元素的序列中切m - 1刀，对于每两个元素之间的间隙，我们都有两种「选择」，切一刀，或者不切。

你看，这不就是标准的回溯暴力穷举思路嘛，我们根据穷举结果去计算每种方案的最大子数组和，肯定可以算出答案。

但是回溯的缺点就是复杂度很高，我们刚才说的思路其实就是「组合」嘛，时间复杂度就是组合公式：

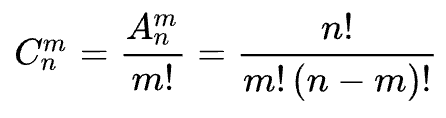
时间复杂度其实是非常高的，所以回溯算法不是一个好的思路，还是得上二分查找技巧，反向思考这道题。

现在题目是固定了m的值，让我们确定一个最大子数组和；所谓反向思考就是说，我们可以反过来，限制一个最大子数组和max，来反推最大子数组和为max时，至少可以将nums分割成几个子数组。

比如说我们可以写这样一个split函数：

//在每个子数组和不超过max的条件下， //计算nums至少可以分割成几个子数组 intsplit(int[]nums,intmax);

比如说nums = [7,2,5,10]，若限制max = 10，则split函数返回 3，即nums数组最少能分割成三个子数组，分别是[7,2],[5],[10]。

如果我们找到一个最小max值，满足split(nums, max)和m相等，那么这个max值不就是符合题意的「最小的最大子数组和」吗？

现在就简单了，我们只要对max进行穷举就行，那么最大子数组和max的取值范围是什么呢？

显然，子数组至少包含一个元素，至多包含整个数组，所以「最大」子数组和的取值范围就是闭区间[max(nums), sum(nums)]，也就是最大元素值到整个数组和之间。

那么，我们就可以写出如下代码：

/*主函数，计算最大子数组和*/ intsplitArray(int[]nums,intm){ intlo=getMax(nums),hi=getSum(nums); for(intmax=lo;max<= hi; max++) {         // 如果最大子数组和是 max，         // 至少可以把 nums 分割成 n 个子数组         int n = split(nums, max);         // 为什么是 <= 不是 == ？         if (n <= m) {             return max;         }     }     return -1; } /* 辅助函数，若限制最大子数组和为 max， 计算 nums 至少可以被分割成几个子数组 */ int split(int[] nums, int max) {     // 至少可以分割的子数组数量     int count = 1;     // 记录每个子数组的元素和     int sum = 0;     for (int i = 0; i < nums.length; i++) {         if (sum + nums[i] >max){ //如果当前子数组和大于max限制 //则这个子数组不能再添加元素了 count++; sum=nums[i]; }else{ //当前子数组和还没达到max限制 //还可以添加元素 sum+=nums[i]; } } returncount; } //计算数组中的最大值 intgetMax(int[]nums){ intres=0; for(intn:nums) res=Math.max(n,res); returnres; } //计算数组元素和 intgetSum(int[]nums){ intres=0; for(intn:nums) res+=n; returnres; }

这段代码有两个关键问题：

1、对max变量的穷举是从lo到hi即从小到大的。

这是因为我们求的是「最大子数组和」的「最小值」，且split函数的返回值有单调性，所以从小到大遍历，第一个满足条件的值就是「最小值」。

2、函数返回的条件是n <= m，而不是n == m。按照之前的思路，应该n == m才对吧？

其实，split函数采用了贪心的策略，计算的是max限制下至少能够将nums分割成几个子数组。

举个例子，输入nums = [2,1,1], m = 3，显然分割方法只有一种，即每个元素都认为是一个子数组，最大子数组和为 2。

但是，我们的算法会在区间[2,4]穷举max，当max = 2时，split会算出nums至少可以被分割成n = 2个子数组[2]和[1,1]。

当max = 3时算出n = 2，当max = 4时算出n = 1，显然都是小于m = 3的。

所以我们不能用n == m而必须用n <= m来找到答案，因为如果你能把nums分割成 2 个子数组（[2],[1,1]），那么肯定也可以分割成 3 个子数组（[2],[1],[1]）。

好了，现在 for 循环的暴力算法已经写完了，但是无法通过力扣的判题系统，会超时。

由于split是单调函数，且符合二分查找技巧进行优化的标志，所以可以试图改造成二分查找。

那么应该使用搜索左侧边界的二分查找，还是搜索右侧边界的二分查找呢？这个还是要看我们的算法逻辑：

intlo=getMax(nums),hi=getSum(nums); for(intmax=lo;max<= hi; max++) {     int n = split(nums, max);     if (n <= m) {         return max;     } }

可能存在多个max使得split(nums, max)算出相同的n，因为我们的算法会返回最小的那个max，所以应该使用搜索左侧边界的二分查找算法。

现在，问题变为：在闭区间[lo, hi]中搜索一个最小的max，使得split(nums, max)恰好等于m。

那么，我们就可以直接套用搜索左侧边界的二分搜索框架改写代码：

intsplitArray(int[]nums,intm){ //一般搜索区间是左开右闭的，所以hi要额外加一 intlo=getMax(nums),hi=getSum(nums)+1; while(lo< hi) {         int mid = lo + (hi - lo) / 2;         // 根据分割子数组的个数收缩搜索区间         int n = split(nums, mid);         if (n == m) {             // 收缩右边界，达到搜索左边界的目的             hi = mid;         } else if (n < m) {             // 最大子数组和上限高了，减小一些             hi = mid;         } else if (n >m){ //最大子数组和上限低了，增加一些 lo=mid+1; } } returnlo; } intsplit(int[]nums,intmax){/*见上文*/} intgetMax(int[]nums){/*见上文*/} intgetSum(int[]nums){/*见上文*/}

这段二分搜索的代码就是标准的搜索左侧边界的代码框架，如果不理解可以参见前文二分查找框架详解，这里就不展开了。

至此，这道题就通过二分查找技巧高效解决了。假设nums元素个数为N，元素和为S，则split函数的复杂度为O(N)，二分查找的复杂度为O(logS)，所以算法的总时间复杂度为O(N*logS)

责任编辑：lq