如何为数字通信接收器指定ADC

本文的目标是提供方法和指导，以便在必须将模数转换器 (ADC) 放置在数字通信接收器中时指定模数转换器 (ADC)。在这种情况下，由于所涉及信号的性质，规范过程需要特别注意。信道噪声和干扰的存在使任务复杂化。在本文中，考虑了最重要的问题，例如噪声预算、线性度要求和时序抖动以及相位噪声。为了简化读者的理解过程，每个给定的规范都提供了数值示例。

噪音预算

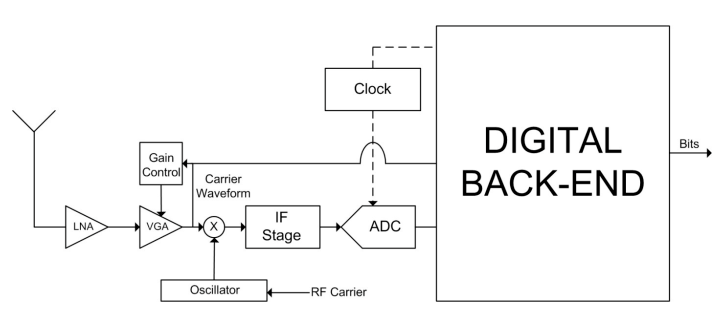
现代数字接收器必须执行滤波、频谱转换和模数转换等第一层任务。接收器还必须执行一些估计接收信号的未知参数（例如幅度、频率和定时对齐）所需的第二层任务。图 1 显示了典型数字接收机中第一层和第二层处理的框图。模数转换器对模拟中频 (IF) 滤波器的输出进行采样，该滤波器由数字下变频器 (DDC) 下变频到基带。然后，基带信号由抽取滤波器向下采样，最后在匹配滤波器中进行处理，以最大化呈现给检测器的样本的信噪比 (SNR)。该接收器的数字信号处理 (DSP) 部分包括载波对齐、定时恢复、信道均衡、自动增益控制、SNR 估计、信号检测和干扰抑制模块。由于接收器包含模拟硬件组件，它还包含许多第三层 DSP 模块，以抑制由不完美模拟模块形成的不希望有的伪像。

通常通过查看输出端的误码率 (BER) 来考虑此类接收器的性能。BER 取决于输入信号的 SNR。叠加在信号上的噪声功率有两个主要来源：信道和硬件设备。

ADC 是接收器的关键组件之一。它对模拟输入信号进行采样，并将采样传送到接收器的基于 DSP 的部分，该部分处理诸如基带移位、解调和信道均衡等任务。

接收信号时，由于信道引起的衰减，其信噪比（SNR）很低；通常它接近背景噪声设置的限制。接收器前端（包括 ADC）的目标是捕获这个微弱信号并将其传递到接收器的数字部分，从而增加最小的退化（实现损失）。然而，由于某些降级是不可避免的，系统设计人员创建了一个系统阵容，其中为接收器的每个模块分配了一定的噪声预算。设计人员知道硬件设备可以添加到输入信号的最大噪声量，并根据输入频谱的特性和技术限制，决定如何在数字接收器中运行的不同处理模块之间分配噪声。

请注意，输入信号最容易受到接收器前端的附加噪声的影响，并且随着放大而变得不那么敏感。出于这个原因，大部分接收器噪声预算分配给前端模块，例如低噪声放大器 (LNA)，而后端模块（例如 ADC）或后面的数字模块通常会收到较小的噪声分配。

例如，假设输入信号的 SNR 为 14dB，接收器所需的最小 SNR 为 12dB。然后系统可以将信号最大降低 2dB，这必须在不同的块之间进行拆分。假设已将 ADC 的噪声分配选择为最大 0.2dB（这意味着 ADC 可使 SNR 降低 0.2dB，而接收器的所有其他设备可使信号降低剩余的 1.8dB），则 SNR ADC 必须是

其中 SNRin 是接收信号的信噪比。

请注意，分配给 ADC 的总 SNR（以 dB 为单位）是其所有损伤

（噪声、谐波失真和时钟相位噪声）的组合。设计人员决定

在这三者之间平均分配ADC分配，使各自的规格

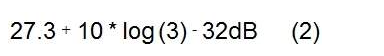
ADC 信噪比应针对单个正弦波指定，该正弦波的幅度与器件的满量程相匹配，该正弦波受整个奈奎斯特带宽上的 ADC 热噪声和量化噪声影响。在我们从未收到纯正弦波的通信场景中，我们调制了携带我们想要传输的信息的正弦波。因此，接收信号的频谱与正弦波的频谱非常不同。我们的目标是了解指定带限信号频谱的 ADC SNR 分配与满量程正弦波的 ADC SNR 之间的关系，以及我们如何从第一个实现第二个。

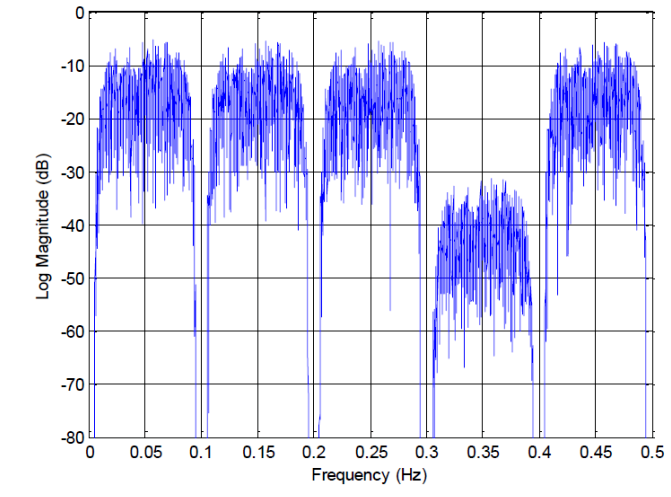
在下文中，我们考虑 ADC 输入信号的典型最坏情况，该信号由四个等幅限带通道和一个弱限带通道组成，这是我们想要检测的通道。这种情况的示例如图 3 所示。强通道的功率为 ADC 的动态范围设置了上限，而来自不同来源的噪声和失真将其限制在下限。

为了计算 ADC SNR 分配，我们需要知道：

• ADC 输入通道的相对功率
• ADC 输入信号的峰均比 (PAR)
• 所需通道的带宽 (bw)
• ADC 采样率 (fs)
• ADC 输入信号的复合（总）功率

ADC 是一个硬限制器。如果输入信号电平在正侧或负侧超过 ADC 代码范围，则 ADC 输出代码将饱和至其最大值或最小值。一旦发生这种削波，输出信号值就会产生很大的误差，对信号 SNR 产生重大影响。确保输入信号电平正确很重要，以免削波发生太频繁。为了避免削波，用户需要知道输入信号的 PAR。该数字用作增益控制环路中的回退，用于监控平均信号电平。在大多数情况下，为了确保输入信号电平适合 ADC，在 ADC 之前将一个或多个可变增益放大器嵌入到接收器中。

在正弦波情况下，为指定 ADC 要做的第一件事是将 ADC 满量程与接收信号电平进行比较。请记住，我们假设输入信号由五个等带宽 （bw=5MHz） 通道组成；其中四个具有高功率电平，而所需通道的功率电平比其他通道低 25dB。我们还假设该信号的 PAR 为 12dB，而根据之前的计算（参见公式（2）），弱通道的 ADC SNR 分配为 32dB，其采样率为 fs=100MHz。

第一步是将弱通道的幅度电平与 ADC 满量程相关联。推理是这样进行的：信号合成功率在ADC满量程（PAR）以下12dB，每个强通道的功率在（10log（4）=6）以下6dB，而弱通道的功率在25dB以下那。综上所述，弱电源的功率比ADC满量程（12+6+25）低43dB。

在这一点上，我们需要计算过采样增益，它考虑到在单个正弦波的情况下需要考虑散布在整个奈奎斯特区的白噪声，而在实际信号情况下只需要考虑噪声下降信号带宽会降低其 SNR。这是真的，因为我们假设在数字域中，在 ADC 之后，有一个滤波器可以去除信号带宽之外的噪声。

可以使用以下公式计算过采样增益：

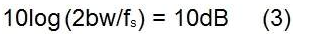
通过了解 ADC SNR 分配 (32dB)、相对于满量程的弱信号幅度 (- ( – 43dB))、过采样增益 (- 10dB) 和正弦波的 PAR 调整因子 (- 3dB) 我们可以计算满量程正弦波的ADC SNR：(32+43-10-3)dB=62dB。

通常 RF 设计人员使用噪声系数 (NF) 而不是 SNR，因此将刚刚计算的信噪比与噪声系数相关联很重要。噪声系数定义为 ADC 的总有效输入噪声功率与仅由源阻抗引起的噪声功率量之比，以 dB 表示（见公式 (4)）。

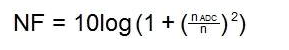
其中 nADC 是 ADC 噪声，可使用公式 (5) 计算

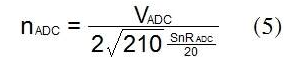
其中 VADC 是差分 ADC 满量程，SNRADC 是单个正弦波的 ADC 噪声分配，其峰峰值幅度恰好填充 ADC 输入范围。SNR ADC 的值通常显示在各种输入频率的数据表上，那么我们必须确保使用与感兴趣的 IF 输入频率相对应的值。此外，我们必须确保基波信号的谐波不包含在 SNR 数中。等式（4）中的参数 n 是源阻抗本身的噪声

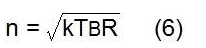
其中 k 是玻尔兹曼常数，T 是以开尔文表示的温度，B=fs/2，R 是阻抗。

请注意，公式 (4) 假设 ADC 的输入带宽限制为 fs/2，滤波器的噪声带宽等于 fs/2。当然，可以进一步对输入信号进行频带限制，从而导致过采样和处理增益。

线性规格

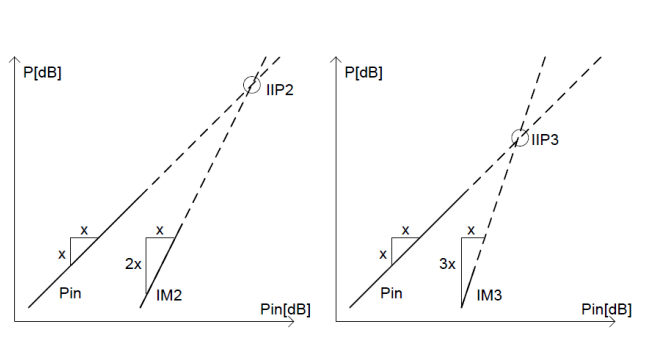
模拟电路通常具有许多不同的性能标准，以便整体系统性能满足所需的规格。对于模数转换器，线性度是一个非常重要的问题，需要注意。它严重影响系统性能。众所周知，如果将正弦波形应用于线性时变系统，输出也将是相同频率的正弦波形，但很可能具有不同的幅度和相位。然而，如果将相同的输入信号应用于非线性系统，则输出信号将具有输入波形谐波处的频率分量，包括基频。最重要的无用谐波分量是二阶和三阶失真分量（通常称为 IM2 和 IM3）。通常，ADC 线性度是使用总谐波失真 (THD) 或使用单个谐波的电平（例如 HD2 和 HD3）来指定的。ADC 设计人员可以通过单音正弦输入信号测试来模拟或测量这些参数。双音测试也常用，并给出 IM2 和 IM3 规格。然而，现实世界的信号与正弦波不同；他们的PAR要高得多，因此这些测试并不准确。

与 IM2 和 IM3 不同，RF 设计人员更喜欢考虑二阶交调点 (IIP2) 和三阶交调点 (IIP3)，它们与 IM2 和 IM3 的关系如图 3 所示。最坏的情况通常是接收弱信号和高功率信号。在这种情况下，我们可以通过用两个正弦波对强信号进行建模来设置双音测试，同时互调产品落在弱有用信号通道上；这里的基本问题是正弦波的峰值是否应该与调制信号的峰值匹配，或者它是否应该与 rms 匹配。这两个选项都不是正确的，因为第一个选项过度指定了 ADC 的线性要求，而第二个选项给出的数字不足以满足实际调制信号的要求。大多数情况下，模拟是解决问题的最佳方法。有时还会执行噪声功率比 (NPR) 测试或缺失音调功率比 (MTPR) 测试，它们更接近于许多现实世界的使用场景。然而，NPR 测试无法使用常用的正弦信号源执行，因此通常会避免使用。在 [2] 中可以找到有关此主题的更多详细信息以及实际示例。

时钟相位噪声和时序抖动

采样时钟边沿与理想位置的位移称为时钟（或定时）抖动。时钟抖动可以是随机的，源于时钟生成电路和时钟分配网络的噪声，也可以是系统性的，因为另一个信号耦合到时钟。但是，它没有描述时钟误差的频谱分布。出于这个原因，有时最好使用相位噪声来代替。

相位噪声可以定义为频谱图或载波周围特定频率范围内噪声功率谱密度的积分。通常使用锁相环 (PLL) 生成 ADC 采样时钟。PLL 的特征相位噪声曲线在载波周围有一个升高的本底噪声区域，其中大部分噪声功率集中。在许多情况下，为接近相位噪声和该区域外的噪声制定单独的规范是有意义的。相位噪声功率或功率谱密度通常表示为相对于以 dBc 为单位的载波功率。这样，相位噪声的单位可以被认为是弧度，因此取决于时钟周期。相位噪声总是在某个载波频率下指定，通常在 PLL 的输出频率上，

分频时钟的相位噪声为：

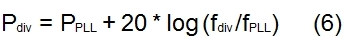
抖动以秒为单位测量，时间是绝对的，当时钟频率被分频时，它的抖动不会改变。请注意，时钟抖动和相位噪声是描述相同现象的两种不同方式。

集成相位噪声被指定为单边带 (SSB) 或双边带 (DSB)。通常相位噪声关于载波是对称的，因此

在下图中，我们给出了当输入信号是一个以 20MHz 为中心的纯正弦波并且考虑的噪声源仅为相位噪声时的 ADC SNR 数值示例。PLL 的集成单边带相位噪声在 1GHz 时设置为 -38dBc。ADC 采样时钟 (100MHz) 是从该信号除以 10 生成的。在这种情况下，时钟的相位噪声轮廓出现在采样信号周围，其幅度为 (20*log(fsig/fclk))。当存在其他噪声源时，该因素必须从总 ADC SNR 进行调整。通过将公式 (7) 与我们为数值示例选择的数字应用，我们发现 ADC 时钟频率下的 DSB 相位噪声为

相位噪声和时序抖动的最终结果应该是一样的。请注意，当我们将正弦波视为输入信号时，噪声功率被视为分布在整个奈奎斯特频带上。在实际情况下，接收信号的带宽是有限的，只需要考虑分布在该频段上的噪声部分。如果噪声在频谱上是白色的（这通常是抖动的假设），则可以使用过采样率（在上一节中计算）来获得 SNR。当噪声不能被视为白噪声（PLL 的接近相位噪声）时，不能使用此方法。这种情况通常发生在所需信号靠近强干扰源或介于更强干扰信号之间时。

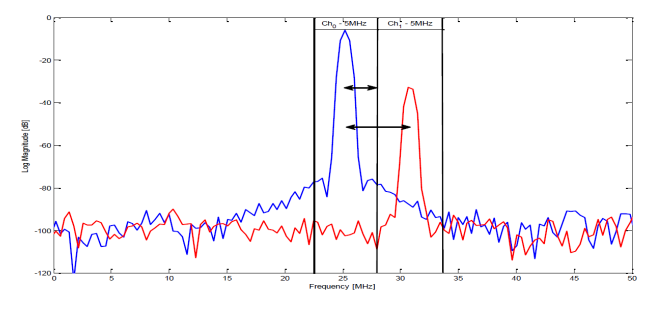
然而，正弦波在设计过程中仍然非常重要。事实上，如果我们在 ADC 的输入端有两个信号，一个比另一个弱得多，宽度均为 5MHz，间隔为 5MHz，强通道的中心频率为 25MHz。弱通道的 SNR 要求为 32dB，强通道的幅度比弱通道高 25dB。驱动时钟的 PLL 的输出频率为 1GHz。在这种情况下，通过在其频率范围的中心用正弦波对更强的信道进行建模，如图 4 所示，我们实现了近似的相位噪声规范，这导致了以下要求：从 2.5MHz 积分的 SSB 相位噪声到 7.5MHz 在 25MHz 时必须小于 57dB (25+32)。相同的计算，在 1GHz PLL 频率下指定，

对于多个强干扰信道之间的弱有用信号支架的情况，我们可以考虑以下数值示例：干扰信道宽5MHz，弱信道以15MHz为中心，其他在20、25、30和35MHz。强通道的幅度比弱通道高 25dB。ADC 采样率为 100MHz，弱通道所需的 SNR 为 32dB。相位噪声假定为白色。在这种情况下，我们使用以信道中心频率的平均值为中心的单个正弦波对信道进行建模，其功率等于四个信道的总功率。再次计算这个虚信号的抖动要求，我们得到：

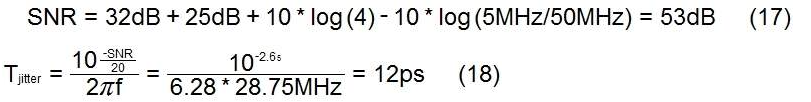
然而，只有通过系统仿真才能获得更准确的抖动规范。

参考

[1] David A. Johns、Ken Martin，“模拟集成电路设计”，John Wiley & Sons, Inc. 纽约。

[2] Mikko Waltari，“如何为数字通信接收器指定 ADC”，可在http://www.iqanalog.com/compan...

[3] Mikko Waltari 和 Kari Halonen，低压和高压电路技术- 速度 A/D 转换器，Kluwer Academic Publishers，2002 年。

编辑：hfy