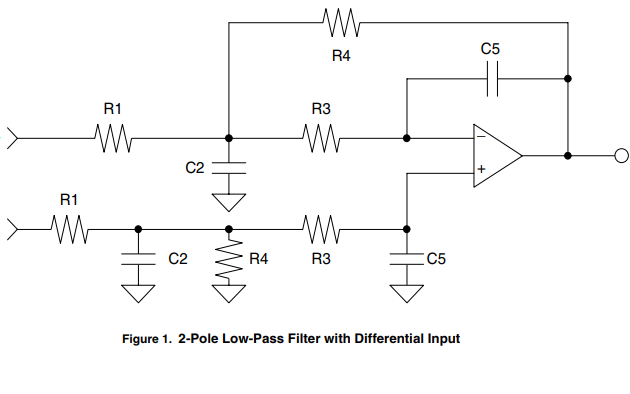
当今的许多数字 DAC 都需要一个具有差分输入的电路,它将消除共模误差、减少由 delta-sigma 调制器产生的带外噪声并产生单端输出。图 1 中的电路包括一个差分输入和一个两极模拟滤波器来实现这些设计要求。本应用笔记概述了选择组件值所需的设计步骤。
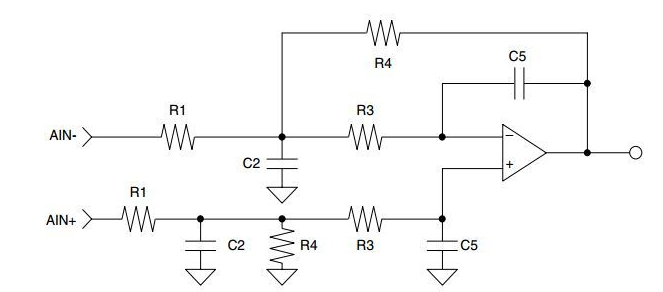
多反馈低通滤波器
请注意图 1 和图 2 中所示的多反馈低通滤波器之间的相似之处。使用多反馈低通滤波器的设计方程可以轻松设计具有差分输入的 2 极点低通滤波器。另外,请注意图 1 和图 3 之间的相似之处。差分输入功能是通过简单地复制滤波器设计中生成的元件值来实现的。
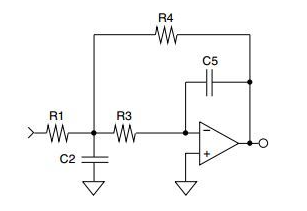
多反馈低通滤波器
设计步骤
步骤 1:确定所需的通带增益 [tex]H _{0}[/tex]。电路参数要求[tex]H_{0}[/tex]的幅度大于或等于1。由于反相运算放大器配置,[tex]H _{0}[/tex] 也为负。
步骤 2:确定最小输入阻抗。
步骤 3:为最终设计选择所需的滤波器类型,Butterworth、Bessel 等,以及其他角频率 [tex]F _{C[/tex]。滤波器响应和转角频率决定了通带相位和幅度响应。滤波器类型决定了极点位置,因此决定了 alpha 和 beta。表 1 列出了几种滤波器类型的归一化极点位置。
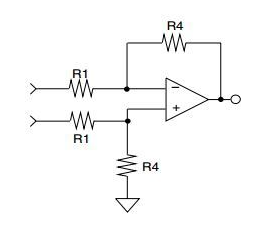
差分输入电路
步骤 4:为 C5 和 C2 选择方便的值。注意在第 5 步中,必须选择 [tex]K[/tex] 和 [tex]H _{0}[/tex] 使得 [tex]sqrt{zeta ^{2}-K(1-H _{0 })}[/tex] 是真实的。
第五步:给定 [tex]F _{C}[/tex], [tex]H _{0}[/tex], [tex]C _{2}[/tex], [tex]C _{5 }[/tex],alpha 和 beta,使用以下公式计算 R1、R2 和 R3:
[tex]zeta = frac{alpha }{sqrt {alpha ^{2}+beta ^{2}}}[/tex]
[tex]omega _{0} = 2pi F _{c} {sqrt {alpha ^{2}+beta ^{2}}}[/tex]
[tex]K=frac{C _{5}}{C _{2}}[/tex]
[tex]R _{1}=frac{R _{4}}{(-H _{0})}[/tex]
[tex]R _{3}=frac{1}{omega _{0}C _{2}[zeta pm {sqrt{zeta ^{2}-K(1- H _{0})}}]} [/特克斯]
[tex]R _{4} = frac{zeta pm {sqrt {zeta _{2}-K(1-H _{0})}}}{omega _{0}cdot C _{5}}[/特克斯]
步骤 6:查看电阻器和电容器值。希望保持足够大的电容器值以最小化杂散电容的影响。可能需要调整在步骤 4 中选择的电容器值以达到此要求。还要验证 R1 是否大于所需的最小输入阻抗。
第七步:第五步计算出来的电阻值一般都不是标准值。选择最接近计算值的标准值。这不会对滤波器特性造成大的变化,因为金属膜电阻器可以以大约 2.5% 的增量提供,这允许选择接近计算值的元件。但是,建议使用选定的值,使用步骤 5 中的公式计算实际滤波器参数。
步骤 8:从单端电路到差分电路的转换需要复制同相输入中 R1、C2、R3、R4 和 C5 的值,如图 1 所示。
编辑:hfy
-
低通滤波器
+关注
关注
14文章
485浏览量
47636 -
dac
+关注
关注
43文章
2320浏览量
192040 -
调制器
+关注
关注
3文章
875浏览量
45488
发布评论请先 登录
相关推荐
解读用于通信系统的差分滤波器
差分滤波器布线需要注意的8个问题
差分滤波器截止频率应该是多少?
通信系统中,差分滤波器如何布局?
具有高SNR和差分输入的无滤波器的D类放大器
带差分输入的双极滤波器DAC输出滤波器LPF的详细设计说明免费下载
具有集成ESD保护功能的差分通道共模 EMI 滤波器-PCMFXHDMI2S_SER





 浅谈差分输入的 2 极滤波器设计
浅谈差分输入的 2 极滤波器设计










评论