作者: 安德鲁·卡特(Andrew Carter)
磁场将对单个运动电荷施加力,并且还将对电流(运动电荷的集合)施加力。长度为l的导线在磁场B中承载电流I时遇到的力用以下公式表示。
[tex] F = ILB sin Theta [/ tex]
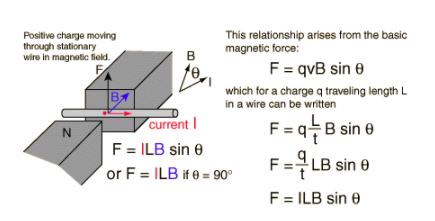
载流导线上的磁力垂直于导线,磁场的位置由右手定则给出。
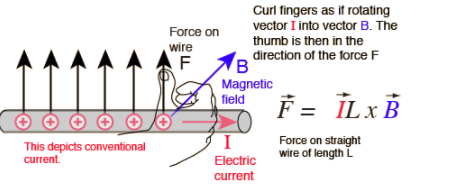
如果电流与磁场之间的夹角为texB [/ tex];[tex] B = 0 [/ tex],然后[tex] sinbeta = 0 [/ tex],[tex] F = 0 [/ tex],[tex] beta = 180 [/ tex],然后[tex] sinbeta = 0 [/ tex],[tex] F = 0 [/ tex],[tex] beta = 90 [/ tex],然后[tex] sinbeta = 1 [/ tex],[tex] F = Bil [/ tex]。因此,如果电流和磁场的方向彼此平行,则不会在导线上施加力。
作用在带电粒子上的力
上面解释了作用在电流上的力。电流是由带电粒子的运动产生的。因此,载流线上的力是该电流作用在每个带电粒子上的力的总和。如果粒子的电荷为q,速度为v,并且位于具有强度B的力作用在该粒子上的磁场中,则β是速度与磁场之间的夹角,公式为:[tex] = qvBsinbeta [ / tex]。
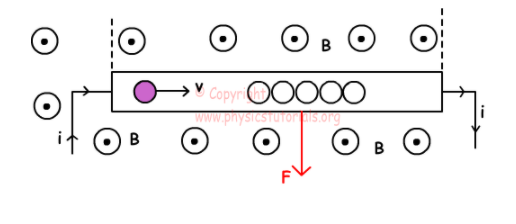
发生条件:
1.如果tex v =0π/ tex,则tex F =0π/ tex,在磁场中没有力施加在静止粒子上。
2.如果∑β = 0 [/ tex],则∑sin0 = 0 [/ tex]和∑F = 0 [/ tex]。
3.如果tex = 180 [/ tex],则ssin180 = 0 [/ tex],且texF = 0 [/ tex],磁场线和粒子的速度彼此平行,那么就没有力了。
4.如果[β] = 90 [/ tex],则[αsin90= 1] / [tex],[f] F = qvB [/ tex]。v
条件发生:
1.如果v = 0,则F = 0磁场中没有力作用在静止粒子上。
2.如果beta = 0,则sin0 = 0,F = 0
3.如果beta = 180,则sin180 = 0,F = 0,磁场线和粒子的速度彼此平行,则没有力施加。
4.如果beta = 90,则sin90 = 1,F = qvB
电线上相互承载电流的力
它表明,同一方向上的电流会相互吸引,因为它们会产生相反的磁场。另一方面,相反方向的电流彼此排斥,因为它们产生具有相同方向的磁场。使用公式,我们可以找到施加在每个力上的力。
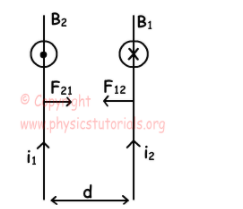
[tex] F = B_1i_2I = 2kfrac {i_1i_2} {d} I [/ tex]
其中,tex1 [/ tex]是导线的长度,tex [dtex // tex]是导线之间的距离。
示例问题:
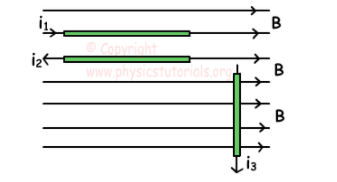
如果将texI_2 [/ tex]放置在恒定磁场中,则求出作用在电流texI_1 [/ tex]上的磁力的方向。
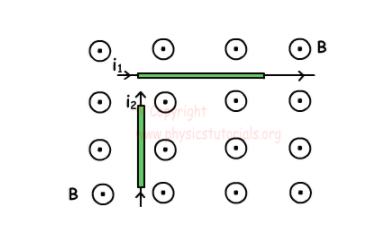
解决方案:
因此,遵循右手定则,答案显示在下面的i中;
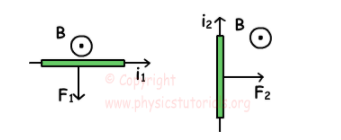
霍尔效应
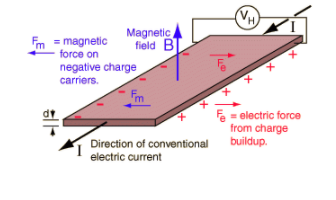
霍尔效应是对电荷移动产生的作用力的一种很好的应用。这也是测量磁场强度的常用方法。薄扁平导体两侧的电荷积聚将平衡这种电磁影响,从而在导体的两侧之间产生可测量的电压。这种可测量的横向电压的存在称为霍尔效应。
霍尔系数表示为感应电场与电流密度和磁场乘积之比。它具有制成导体的材料的特征,其值取决于构成电流的电荷载流子的类型,数量和特性。
编辑:hfy
-
霍尔效应
+关注
关注
5文章
464浏览量
43175
发布评论请先 登录
相关推荐
电感在电路中的作用 电感对电流的影响分析
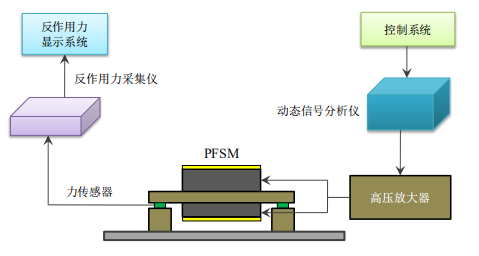
安泰高压放大器在大口径压电倾斜镜的反作用力研究中的应用




 磁场中电流的作用力 电线上相互承载电流的力
磁场中电流的作用力 电线上相互承载电流的力










评论