一些经验公式
在上面给大家展示的这张图其实是非常有代表意义的:
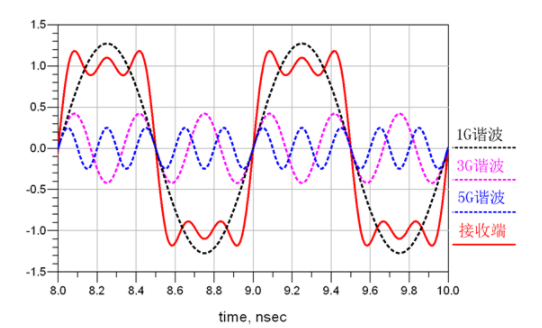
这是一个1GHz的信号,上升沿大概在0.1ns左右。大家想到了什么?
五倍频谐波合成一个波形,上升沿时间为信号周期的十分之一,符合我们一切对信号完整性的预期。
该信号五倍频率处的这个谐波称之为最高次有效谐波,我们前文中说的集总参数与分布参数界限的λ/20,指的就是最高次有效谐波的λ/20。所以一个1GHz的信号(注意这里说的是信号,不是正弦波),通常他的λ/20是60mil。
但是否每个波形的最高次有效谐波都是信号的五倍频呢?并不一定,大家看下面两幅图:
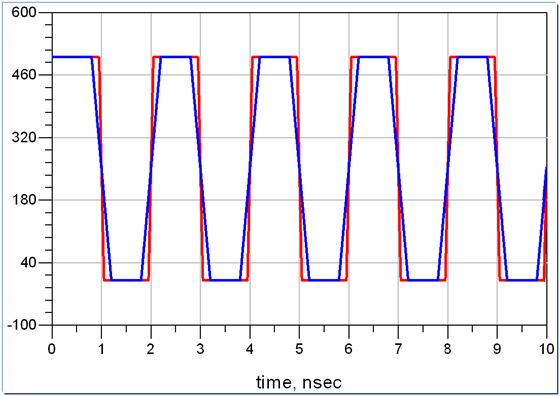
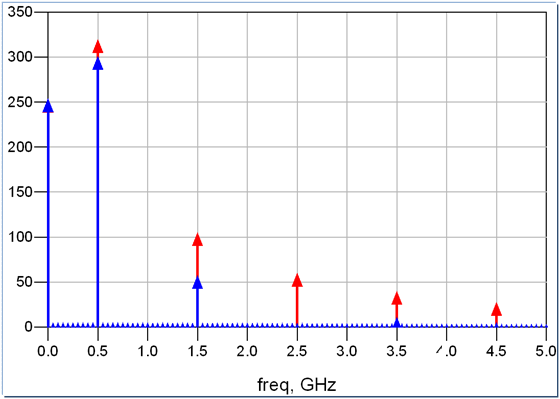
这是两个频率为500MHz的信号,他们周期相等,幅值也相等,但是上升沿不一样。很明显,上升沿较抖的红色信号直到9倍频处还有较为明显的频率分量,而上升沿较缓的蓝色信号在三倍频以后的频率分量就非常少了。
什么时候会出现这种状况呢,不是说好了上升沿时间为信号周期的十分之一吗?
由于工艺的不断更新换代,芯片的die电容不断减小,现在大量的100MHz信号的上升沿达到了0.2ns甚至更少,高速先生不久前就碰到过66MHz的信号反射非常严重的。
同样是因为工艺的原因,按照上升沿时间为信号周期的十分之一计算的话,25Gbps信号的上升时间应为8ps,臣妾做不到啊!所以在802.3bj中,要求的25G信号的上升沿为9.6ps(20%-80%)。而在现在的高速无源链路上只关心到信号中心频率的两倍频处,再高的频率分量由芯片来给你保证了。
为了辅助我们得出最高次有效频率,我们还有这些经验公式:0.35/Tr,0.5/Tr••••••其中Tr单位使用ns的话,得到的频率为GHz,两个公式的区别在于对最高次有效谐波定义的严格与否。
等等!各位看官不要走!如果您觉得这样计算最高次有效谐波的波长再除以二十再跟传输线长度来进行对比来判断是集总参数还是分布参数再去决定是否考虑传输线效应太麻烦的话,这里还有个最简单的:
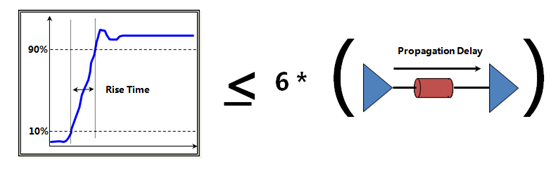
就是这个了,如果上升时间小于六倍的传输延时,我们需要考虑传输线效应,称之为高速。
最后,让我们来对比一下两种方法算出来的分布参数与高速有何不同,拿我们最开始的DDR3的波形举例:
上升时间Tr为100ps;
高速的临界条件为传输延时为16.6ps;
16.6ps传输的长度为100mil;
100mil为3GHz正弦波的λ/20;
3GHz约等于使用0.35/Tr来算最高次谐波3.5GHz;
如果使用0.5/Tr来算最高次谐波的话,他的最高次谐波为5GHz;
回到文章顶部看我们最开始分享的那张图••••••
其实我们用有效频率的二十分之波长来定义分布/集总参数与用六分之上升时间来定义高速/低速信号是完全一样的东西啊。
路的反射
文章未动,公式先行:
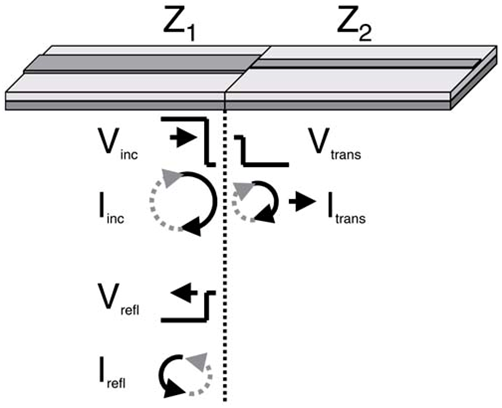
inc ──入射 trans ──传输 refl── 反射
当信号穿越阻抗不连续的点时,会产生反射电压与电流,从而使得分界面两边的电压和电流相等(基尔霍夫定律)。
这样就有如下公式:

其中,由欧姆定律有:
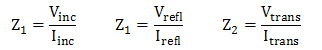
将基尔霍夫电流定律的电流用V/Z替代后:
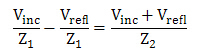
将V_trans替换后:
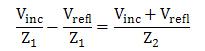
由该公式我们可以得出:
反射系数
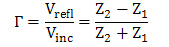
传输系数
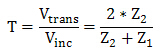
在这里给大家自爆一下高速先生小时候学习过程中做过的笔记:
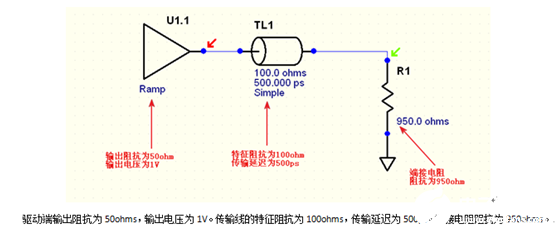
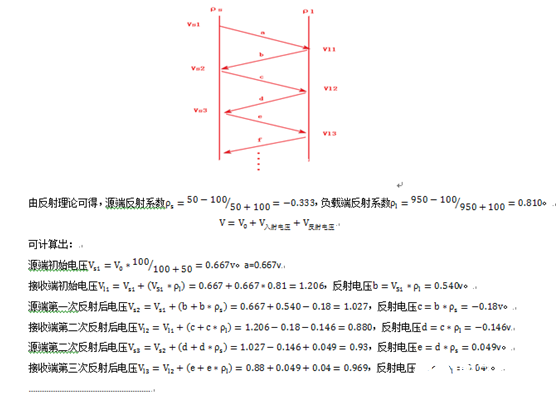
对于理工科来说,一些从数学上去理解问题的过程是必不可少,也是最直观的。
高速先生也和大家一样,学习反射都是从手算反弹图开始的。同样的,小高速先生 在画出反弹图之后曾经觉得自己懂反射了。
可是转念一想,还是发现了很多无法理解的问题:
为什么测试时在通道中间测试到的波形有回沟,而在终端测试到的波形又是好的?
Breakout区域有一次阻抗不连续,但走出该区域之后,走线从细变宽,会增加一次反射,那是不是全程按照breakout区域走线会比较好?源端匹配电阻是不是也增加了一次反射?
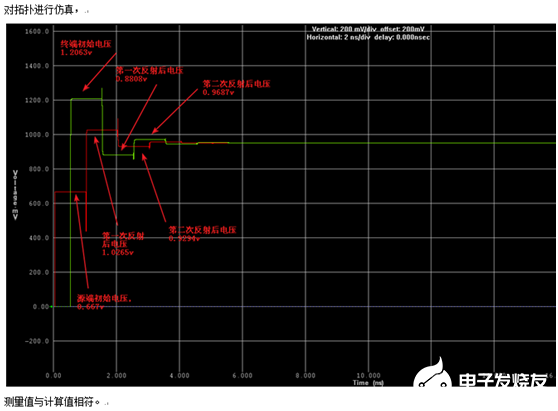
是的,其实这些用一句“传输线很短的时候反射掩盖在上升沿中了”就可以解释。但是到底是怎么掩盖在上升沿中的?
我们发现在上方的反弹图中传输延时远远大于信号的上升时间,在计算反射时我们用的电压实际上是信号高电平的电压,并没有关注上升沿过程中其他电平的状态,但实际上的情况并不是这样,可是如果我们如果把上升沿的状态加入算式中,那这游戏可就没法玩了。
编辑:hfy
-
DDR3
+关注
关注
2文章
276浏览量
42258 -
谐波
+关注
关注
7文章
823浏览量
41780
发布评论请先 登录
相关推荐
DDR3、DDR4、DDR5的性能对比
如何选择DDR内存条 DDR3与DDR4内存区别
基于FPGA的DDR3多端口读写存储管理设计
三星和SK海力士下半年停产DDR3内存
华邦倾力挺进DDR3市场,抓住转单商机
全套DDR、DDR2、DDR3、DDR3L、LPDDR3 和 DDR4 电源解决方案同步降压控制器数据表

完整DDR,DDR2,DDR3 和LPDDR3 存储器电源解决方案同步降压控制器数据表

完整的DDR2、DDR3和DDR3L内存电源解决方案同步降压控制器TPS51216数据表

适用于DDR2、DDR3、DDR3L和DDR4且具有VTTREF缓冲基准的TPS51206 2A峰值灌电流/拉电流DDR终端稳压器数据表

具有同步降压控制器、2A LDO和缓冲基准的TPS51916完整DDR2、DDR3、DDR3L和DDR4存储器电源解决方案数据表

具有同步降压控制器、2A LDO和缓冲基准的TPS51716完整DDR2、DDR3、DDR3L、LPDDR3和DDR4内存电源解决方案数据表

完整的DDR、DDR2和DDR3内存电源解决方案同步降压控制器数据表





 仿真反射详解:DDR3的时钟信号
仿真反射详解:DDR3的时钟信号












评论