01导读
作为拓扑材料的一个重要研究分支,拓扑能带简并的研究起源于在周期性材料中寻找外尔和狄拉克准粒子。由于周期系统的晶体空间群比均匀时空支持更丰富的能带简并结构,因此在周期系统中存在着超越高能物理所研究的准粒子态。通常人们认为光子晶体中整数自旋空间群可完整描述电磁波的能带简并和拓扑结构。
近日,华中科技大学陈云天副教授团队,香港科技大学陈子亭教授团队等课题组共同合作,揭示了一种隐藏于麦克斯韦方程组中光学系统特有的对称性,发现了一种由隐藏对称性保护的全新的三重简并点(称为拓扑节线连结点),及该频点出新奇的光学现象。相关成果以“Hidden-symmetry-enforced nexus points of nodal lines in layer-stacked dielectric photonic crystals”为题发表在Light: Science & Applications。
该文作者发现如果各向异性介电张量的不同元素具有比晶格元胞更小的分数周期,则麦克斯韦方程可展现出超越空间群的隐藏对称性,此对称性保证了多条能带之间的拓扑节线始终会相交于一对三重简并点。
这种被称为拓扑节线连结点的新型三重简并准粒子是动量空间中有别于狄拉克磁单极的一类新型磁单极子。利用三重简并点附近的特殊各向异性色散特征,研究发现该点处具有奇特的自旋1圆锥衍射效应,可实现最大拓扑荷为2的光涡旋态。
02研究背景
对称性原理是现代物理学发展的基石,在人们揭示自然规律和建立物理定律的过程中起到了关键作用。假如没有对称性原理的应用,很难想象物理学近两百年有如此巨大的发展。对称性原理的一个重要应用是揭示了每一个守恒量的背后都有一种相应的对称性存在,比如动量守恒本质上是空间平移对称性的结果。另一方面,以规范变换对称为代表的隐藏对称性对于揭示基本粒子间的相互作用起到了关键的作用。如2004诺贝尔物理学奖获得者David Gross所说,现代物理前沿中的研究重点就是探寻极小尺度下新的隐藏对称性。 在拓扑物理研究中,对称性同样发挥着极其重要的作用。物理系统的对称性不仅决定了拓扑绝缘相和拓扑简并的分类,对于基于拓扑效应的新型光电器件的设计和探索也有指导意义。
在拓扑光子学早期的开拓性研究工作中,研究人员通常是寻找与电子拓扑态相对应的电磁效应。光子作为玻色子,与电子有本质的区别,近年探索光学系统自身独有的对称性导致的拓扑效应逐渐受到人们的重视。
例如利用电磁对偶对称性,可实现类似于电子系统的Kramers简并。由于电磁对偶对称性对材料介电常数和磁导率的关系有极严格的限制,这对拓扑光学器件的实用化造成了障碍。
在普通的电介质材料中是否也蕴涵着可导致非平凡拓扑性质的隐藏对称性呢?这正是本文要回答的问题。
03创新研究
该工作揭示了一种隐藏于麦克斯韦方程组中光学系统特有的对称性,发现了一种由隐藏对称性保护的全新的三重简并点(称为拓扑节线连结点),及该频点出新奇的光学现象。
定态麦克斯韦方程组可以简单表示为一个广义本征值问题N^(r)ψ=ωM^(r)ψ,由于所有空间群操作都不改变旋度矩阵N^,所以空间群的对称性只要求本构张量M^(r)在空间群变换下不变。如果把麦克斯韦方程改写为哈密顿量形式H^(r)ψ=ωψ,H^(r)=M^(r)-1N^(r),不难发现,麦克斯韦方程所满足的对称性A^只要求H^(r)在对称操作下不变,而不需要N^和M^各自满足对称条件。
这意味传统的空间群可能只涵盖了光学系统对称性的冰山一角,也意味光学系统中可能存在大量未被发现的对称性值得研究和利用。
本文设计了一个由各向异性电介质板堆叠而成的光子晶体结构来展示这种隐藏对称性及其对能带的影响,光子晶体周期性来源于同种各向异性电介质的光轴周期性旋转(图1)。
图1 各向异性层堆叠式的光子晶体及其能带
本文的研究发现由于介电张量的各个分量可以具有比光子晶体元胞更小的周期(原胞周期的分数),导致该系统具有一个超出空间群的广义的分数螺旋对称性。这个隐藏对称性与时间反演对称性一起保证了除最低两条能带之外的所有能带都沿着kz轴(ΓZ)方向具有二重简并,进而构成一类横贯kz轴的新型拓扑节线(称之为“类Kramers”拓扑节线)。
由于隐藏对称性的存在,可证明了光子晶体具有比空间群对称条件约束下更高的能带连通性。考虑到电介质光子晶体的最低一对能带必定经过光锥原点(ω=|k|=0),可证明最低阶的类Kramers拓扑节线一定和另外两条受镜面对称保护的拓扑节线环相交于一对三重简并点(图2),称为拓扑节线连结点(nexus point)。
图2 隐藏的1/4螺旋对称性对能带连通性的影响
类比实空间中的电磁场,贝里曲率通量(Berry flux)可看作动量空间中的磁通量,而外尔点作为贝里磁通量的辐射源对应于实空间中的狄拉克磁单极子。在本文研究的系统中,所有的贝里曲率磁通量都被束缚在拓扑节线上,所以拓扑节线可认为是动量空间中的“宇宙弦”,而节线连结点作为“宇宙弦”的交汇点构成了动量空间中一类有别于外尔点的新型磁单极子。 如图3所示,能带在三重简并连结点附近呈现出不同寻常的各向异性色散特征。在ky=0截面上三个能带沿着拓扑节线线性交叉,在kx=0截面上能带结构类似于II型三重简并点。而在kz固定的截面上能带由一对圆锥和一条平带相交形成由二维自旋1哈密顿量描述的二维各向异性类狄拉克锥,在等频率面内也表现出相似的类狄拉克锥色散特征。打破隐藏对称性会导致沿着类Kramers拓扑节线的二重简并打开,节线连结点随之消失,而原先相交的一对拓扑节线环分离为一上一下两条独立的节线环,根据节线附近不同的能带色散,上面一条称为第二类拓扑节线环,下面一条为第三类拓扑节线环。
图3 三重简并连结点附近的能带结构
当光束入射到普通二重简并拓扑节线上时,如光线沿双轴晶体光轴方向入射,会发生经典的圆锥衍射现象,这种衍射效应可由二维的自旋1/2狄拉克方程解释。相比之下,三重简并节线连结点对光的衍射效应呈现出明显不同,由于该频点附近的等频率面形成一个自旋为1的类狄拉克锥,单色光在该点上的动力学可由二维自旋1哈密顿量描述,其中z轴可等效为时间轴,这导致此处入射的光波会经历特殊的自旋1圆锥衍射(图4)。该频点的色散特征导致衍射光束会分成圆锥状衍射环和一束沿z方向笔直传播的两部分光束。
更有趣的是,如果入射光的初始状态是一个spin-1角动量本征态,光束在衍射过程中会发生自旋量子数跃迁,而跃迁前后的自旋角动量之差会转化为衍射环的轨道角动量。当将出射波投影到不同的自旋1本征态上时,会观察到环绕衍射环的光涡旋,光涡旋的拓扑荷由初末态自旋量子数之差决定,因此可取值0,±1和±2。这个效应表明了该三重节线连结点为研究二维自旋1动力学提供了一个新途径。
图4 三重简并连结点处的自旋1圆锥衍射效应
04应用与展望
本文研究了一种受麦克斯韦方程隐藏对称性保护的新型光学三重简并态,也为拓扑能带简并方面的研究带来一些思考和启发。
一方面,文中所揭示的隐藏对称性源于介电张量中不同分量的分数周期性,该性质反映了光子晶体的几何属性,不被传统的空间群所涵盖。因此发展包含这种隐藏对称性的广义空间群理论对研究光子系统具有重要意义。
另一方面,该工作使用的光子晶体结构由单一的各向异性介电材料组成,但其能带特性完全来自于材料内部光轴的非平凡周期旋转。虽然最近的研究表明,通过控制介电极化的方向可以实现人工规范场、Pancharatnam-Berry 几何相位和人工自旋轨道相互作用,但目前对各向异性介质光子晶体的能带拓扑性质的研究还很少。
该研究结果表明,材料的內禀各向异性具有结构各向异性不可替代的特征,因此各向异性介质,如液晶等,为实现电磁场特有拓扑效应提供了新的平台。
责任编辑:PSY
-
光子晶体
+关注
关注
1文章
34浏览量
10702 -
高阶
+关注
关注
0文章
4浏览量
7084 -
对称性
+关注
关注
0文章
5浏览量
5742
发布评论请先 登录
相关推荐
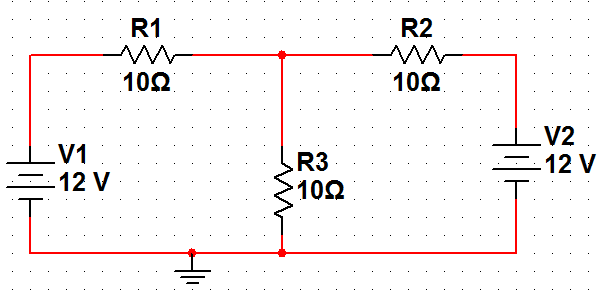
利用对称性化简求解对称电路
运放的哪些参数可以反映出它的不对称性?
对称性加密算法
对称性对傅里叶系数的影响
基于几何对称性的颅骨复原技术
对称性和格点理论在矩量法中的应用
机械结构对称性实例设计




 光子晶体中隐藏对称性与高阶
光子晶体中隐藏对称性与高阶











评论