你可以立刻意识到相位噪声是“相位的噪声”。 那什么是相位呢? 同样,相位的数学定义来自高中数学,如下所示。
相位的定义
红色图和蓝色图具有相同的频率和振幅,唯一的区别是相位。 在图 c 中,你可以清楚地看到。 如果你在时域中看到一个信号,相位差会导致信号的延迟或提前。
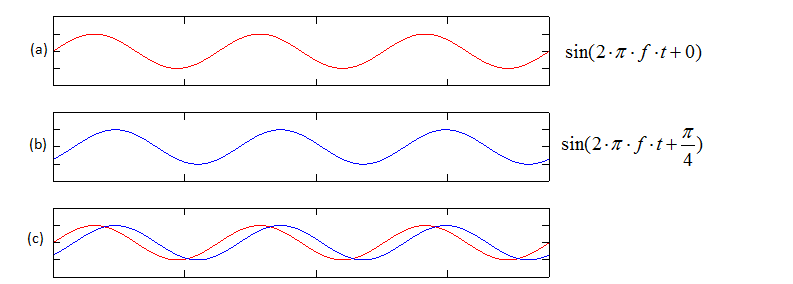
现在我们来考虑一下,信号在频域中是如何随相位变化的。 看看下面的三个情节。 红色图(a)和蓝色图(蓝色)具有相同的频率和振幅,唯一的区别是相位。 我已经提到了时域差异(左列) ,现在让我们看看频域差异(中心列)。 如果你只关注峰值点,你不会发现任何明显的区别之间的蓝色信号和红色信号。 但是如果你仔细观察峰值点旁边的区域,你会发现蓝色信号和红色信号之间有很大的不同。
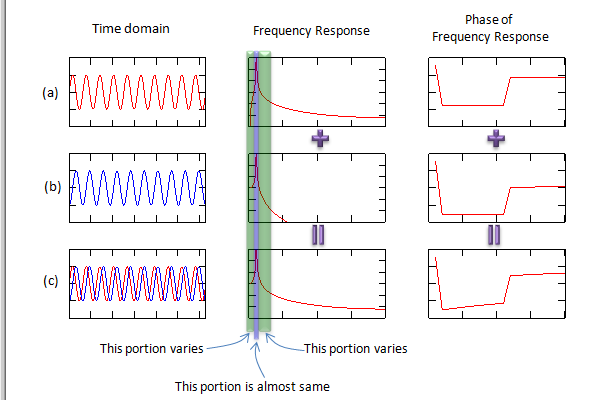
相位噪声是一种信号的意外(无用的)相移噪声。 在上面的描述中,我只比较了两个信号,但实际上噪声信号的相位在一定范围内不断变化。 这就是为什么我们叫它噪音。 (如果相位移动到一个特定的值,并且一直保持不变,就像上面的例子一样,我们不会称之为噪声。 这只是一个很容易纠正的相位变化。 我使用了一个只有两个阶段的案例,只是为了便于解释)。
为什么相位噪声会是个问题?
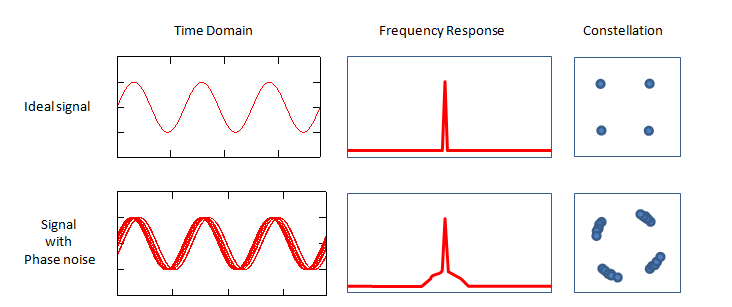
为什么相位噪声会成为问题? 让我们看一系列由相位噪声造成的问题,你就会知道为什么我们要避免相位噪声。 下面图表的顶行显示了一种没有任何噪声(尤其是没有相位噪声)的信号。 看一下时域和频域,假设信号是 QAM 调制的。 然后假设信号受到相位噪声的影响。 如果你在时间域绘制噪声信号,你会得到第二行显示的图。 你们需要注意的是,频率响应。 如果一个信号有相位噪声,你会看到展开裙底的信号如下图中间图所示。 相位噪声会出现在调制以后的星座图中,如右边所示。
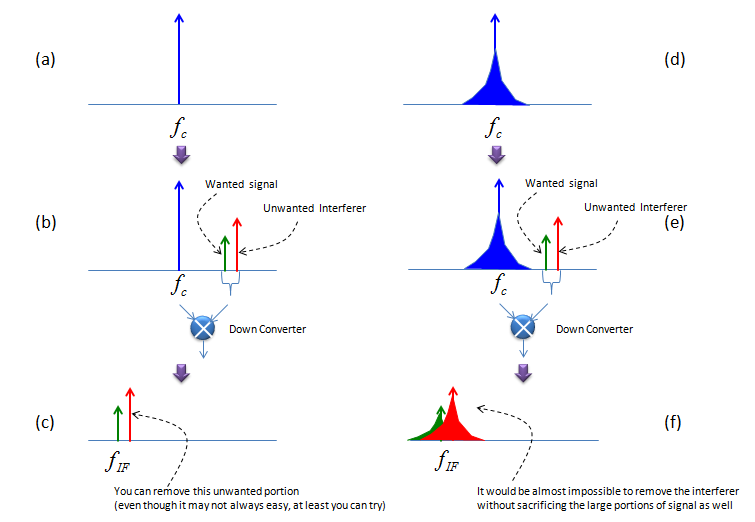
让我们看看由相位噪声引起的另一个问题。 让我们假设你在接收机链上的本机振荡器具有理想的频率响应,如(a)所示,并处于(d)所示的相位噪声之下。 现在这个接收器链接收信号(需要信号)和干扰信号(不需要信号) ,如(b) ,(d)所示。 信号和干扰通过下变频器,问题就从这里开始。 当本地信号没有任何相位噪声时,下变频器后的大部分干扰(例如,使用滤波器)可以消除,因为它们彼此分离,如(c)所示。 但是,当你的本机振荡器有相位噪声,而且(信号 + 干扰)被噪声本机振荡器降低时,结果就会如(f)所示。 由于信号和干扰信号的频率响应都是通过本机振荡器的相位噪声来传播的,因此相干信号的频率响应与信号的频率响应是重叠的。 在这种情况下,几乎不可能完全去除模拟级(例如RF或IF级)中的干扰。 这就是为什么本机振荡器的相位噪声特性如此重要的原因。
还有另外一种情况,相位噪声也会成为问题。 我们假设下面的情况。 在这种情况下,一个非常干净的弱功率信号进入接收机,同时一个强干扰信号进入接收机,在这种情况下,即使信号(我们需要的信号)是干净的,也可能被埋没在附近信号的相位噪声之下,不能被正确解码。
总之,相位噪声在时序上(示波器看到的)是抖动,在频域上看到的是宽裙边,是我们不希望看到的噪声。相位噪声出现在发射本振(TX LO)中会严重影响星座图的EVM,接收本振(RX LO)中会严重影响信号的解调。
责任编辑人:CC
-
噪声
+关注
关注
13文章
1122浏览量
47429 -
相位噪声
+关注
关注
2文章
180浏览量
22874
发布评论请先 登录
相关推荐
什么是相位噪声 相位噪声测试原理分析
雷达脉冲调制信号的绝对相位噪声和加性相位噪声测量解决方案
什么是相位噪声?常见的相位噪声源有哪些?
改进的DAC相位噪声测量
什么是相位噪声?造成相位噪声的原因?
AM噪声、相位噪声测量
如何通过一种系统化方法来量化电源噪声电压电平对相位噪声的影响
相位噪声是什么?相位噪声指标




 为什么相位噪声会成为问题看了就知道
为什么相位噪声会成为问题看了就知道











评论