在直流电路中,功耗仅是直流电压乘以直流电流(以瓦特为单位)的乘积。但是,对于带有无功分量的交流电路,我们必须以不同的方式计算消耗的功率。
电功率是电路中能量消耗的“速率”,因此,所有电气和电子组件及设备都对其可安全处理的电功率量有所限制。例如,一个1/4瓦的电阻器或一个20瓦的放大器,电力可能随直流量或交流量而随时间变化。电路在任何时刻的电量都称为瞬时电量,它由功率等于伏特乘以安培(P = V * I)的众所周知的关系给出。因此,一瓦特(每秒消耗一焦耳的能量的比率)将等于一伏特乘以一安培的伏安乘积。
那么,电路元件吸收或提供的功率就是该元件两端的电压V和流经该元件的电流I的乘积。因此,如果我们有一个电阻为“ R”欧姆的直流电路,则电阻的耗散功率(以瓦特为单位)可以通过以下任一通用公式得出:
其中:V是直流电压,I是直流电流,R是电阻值。
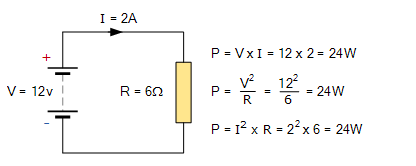
因此,只有当电压和电流同时存在时,电路中的功率才存在,即没有开路或闭路条件。考虑以下标准电阻直流电路的简单示例:
直流电阻电路
交流电路中的电力在直流电路中,电压和电流通常是恒定的,不会随时间变化,因为没有与电源相关的正弦波形。但是,在交流电路中,电压,电流和功率的瞬时值受电源的影响而不断变化。因此,我们无法以与直流电路相同的方式来计算交流电路中的功率,但仍可以说功率(p)等于电压(v)乘以安培(i)。
另一个重要的一点是,交流电路包含电抗,因此存在功率成分,这是由该成分产生的磁场和/或电场造成的。结果是,与纯电阻组件不同,该功率被存储,然后在正弦波形经过一个完整的周期周期后返回电源。
因此,电路吸收的平均功率是一个完整周期内存储的功率与返回的功率之和。因此,电路的平均功耗将是一个完整周期内瞬时功率与瞬时功率的平均值p,瞬时功率p定义为瞬时电压v与瞬时电流i的乘积。请注意,由于正弦函数是周期性且连续的,因此在所有时间内给出的平均功率将与在单个周期内给出的平均功率完全相同。
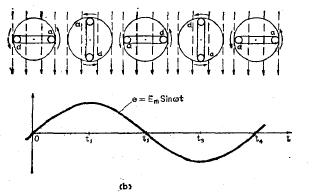
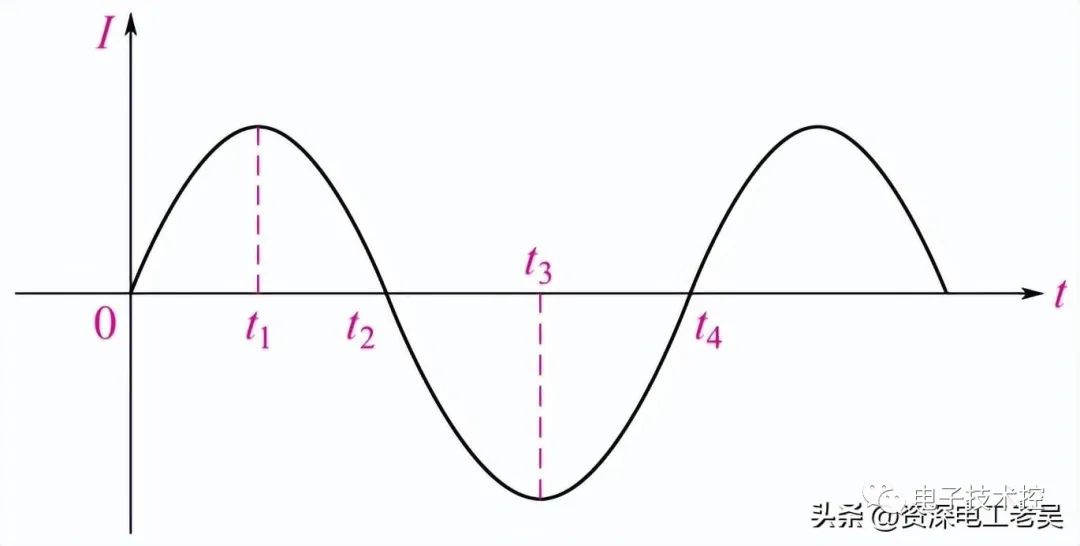
让我们假设电压和电流的波形都是正弦波,因此我们回想一下:
正弦电压波形
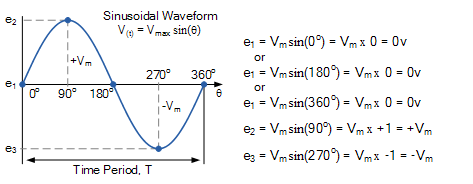
由于瞬时功率是任何时刻的功率,因此:
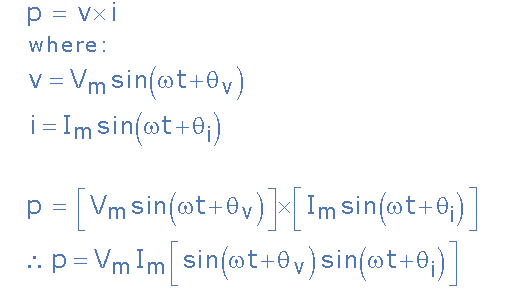
应用以下公式的三角积和和:
和θ =θ v - θ 我入上式(电压和电流波形之间的相位差)给出:
其中V和I分别是正弦波形的均方根(rms)值,v 和i,θ是两个波形之间的相位差。因此,我们可以将瞬时功率表示为:
瞬时交流功率方程
该方程式向我们显示瞬时交流功率具有两个不同的部分,因此是这两个项的总和。第二项是随时间变化的正弦曲线,由于项的2ω部分,其频率等于电源角频率的两倍。但是,第一项是一个常数,其值仅取决于电压(V)和电流(I)之间的相位差θ。
由于瞬时功率会随着时间的变化而正弦曲线的轮廓不断变化,因此很难进行测量。因此,在数学上使用幂的平均值或平均值更方便,也更容易。因此,在固定的周期数内,正弦曲线瞬时功率的平均值简单地表示为:
其中V和I是正弦有效值,而θ(Theta)是电压和电流之间的相角。功率单位为瓦特(W)。
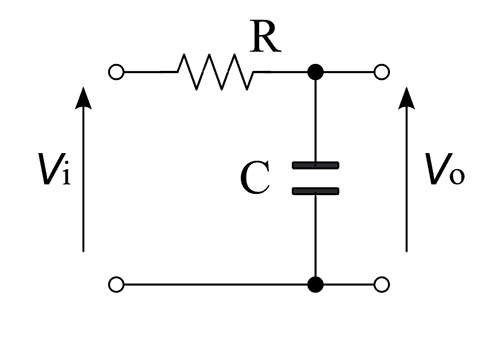
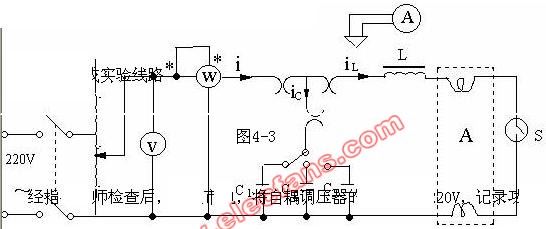
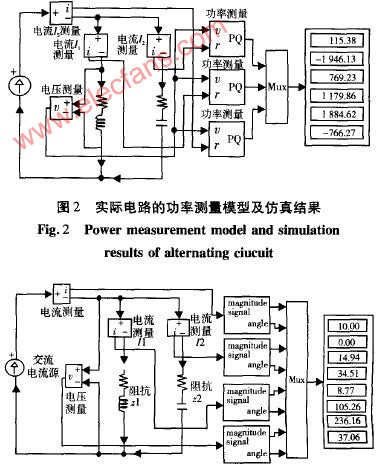
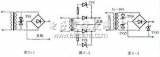
如图所示,也可以使用流过电路的电压V rms或电流I rms,从电路的阻抗(Z)中找到在电路中耗散的交流电源。
责任编辑人:CC
-
电源
+关注
关注
185文章
17969浏览量
252899 -
交流电路
+关注
关注
0文章
185浏览量
28967
发布评论请先 登录
相关推荐
交流电路中电容和阻抗之间的关系,如何计算电容器的阻抗?




 一文详解交流电路中的电源
一文详解交流电路中的电源
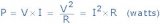











评论