机器学习：线性回归与逻辑回归的理论与实战

1、基本概念

要进行机器学习，首先要有数据。从数据中学得模型的过程称为“学习”或“训练”。其对应的过程中有几个基本术语需要知道。

（1）训练集：模型训练过程中使用的数据称为训练集，其中每个样本称为训练样本。如：D={X1,X2,X3,…,Xm}。

（2）特征向量：对于每个样本如Xi = (xi1, xi2,…xin)是一个n维列向量，表示样本Xi有n个属性。

2、理论

给定由n个属性描述而成的m个数据集为：D={X1,X2,X3,…,Xm}，其中Xi = (xi1, xi2,…xin)。

线性模型是试图学得一个通过属性的线性组合来进行预测的函数，即：

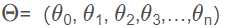其中，其中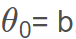。当Θ和b确定之后，模型就得以确认。

2.1 线性回归

2.1.1 什么是回归

若我们欲预测的是连续值，如：房价，则此类学习任务称为“回归”。同理机器学习中还有“分类”任务，即我们欲预测的是离散值，如：“合格”、“不合格”。其中对于二分类任务，称为“正类”、“负类”；涉及多个类别时，则称为“多分类”任务。

在线性模型中，我们分为线性回归与逻辑回归两种模型，下面我们对两种模型分别进行讲解分析。

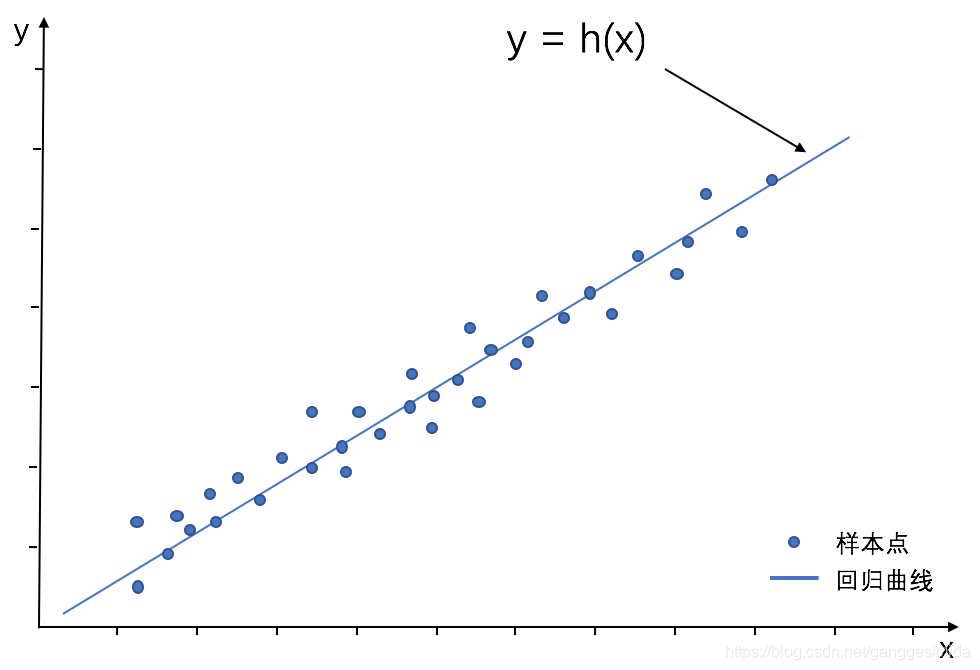
图1 线性回归

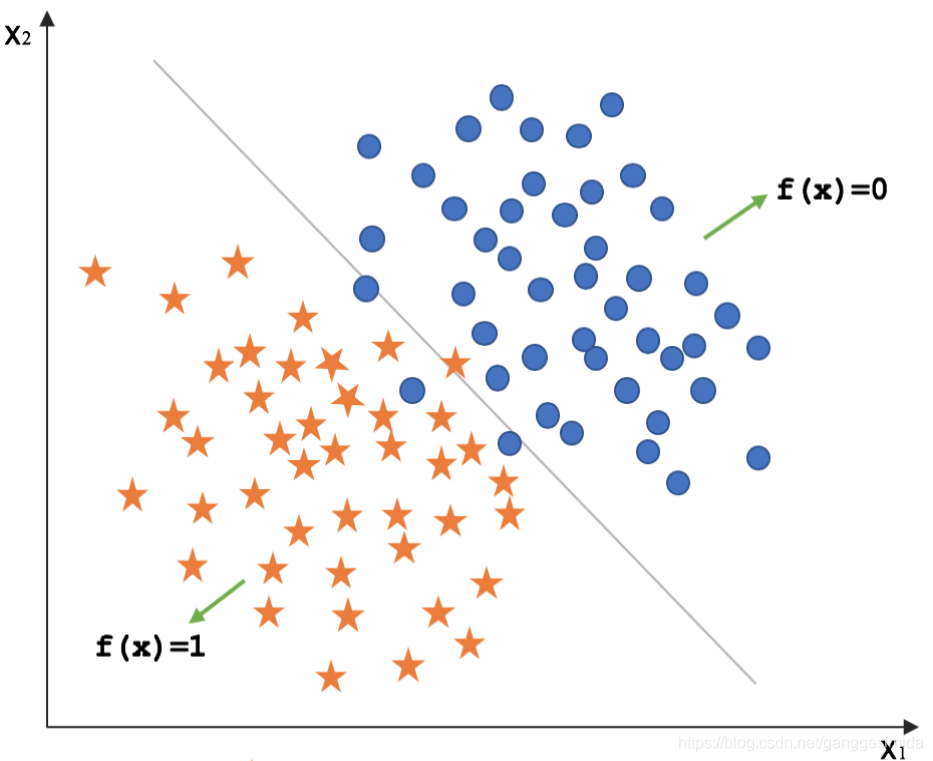
图2 逻辑回归

2.1.2 线性回归推导

1、线性回归试图学得：

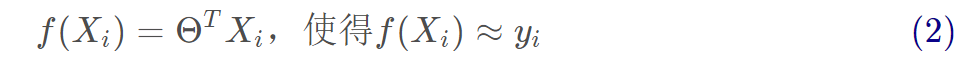
2、参数估计

（1）首先衡量f(X)与Y之间的差别，我们使用均方误差来衡量。

均方误差的推导过程如下：

拟合函数为：

矩阵形式为：

真实值和预测值之间通常情况下是会存在误差的，我们用ε来表示误差，对于每个样本都有：

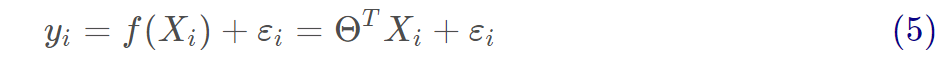
通常我们假设样本空间中全体样本中服从一个未知“分布”，我们获得的每个样本都是独立地从这个分布上采样获得的，即“独立同分布”(iid)。

在这里误差ε是独立并且具有相同的分布，并且服从均值为0，方差为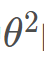的正态分布。

由于误差服从正态分布，那么有：

将(5)代入到(6)可得：

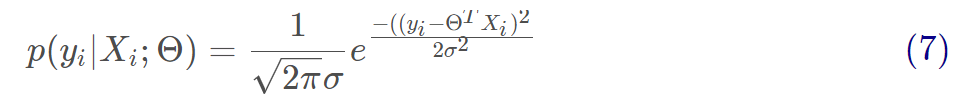
用似然函数进行估计，即求出什么样的参数跟我们给出的数据组合后能更好的预测真实值，有：

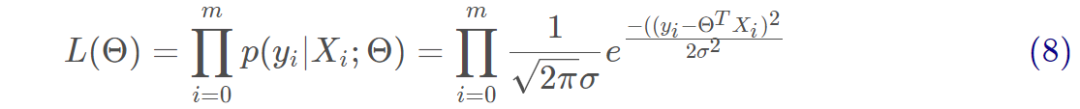
对式8取对数，将连乘转化为加法为：

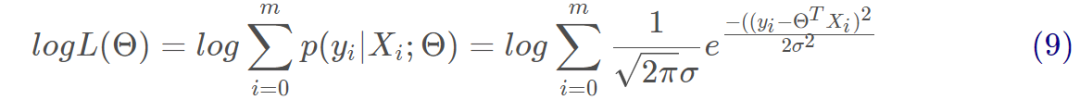
对式9展开化简为：

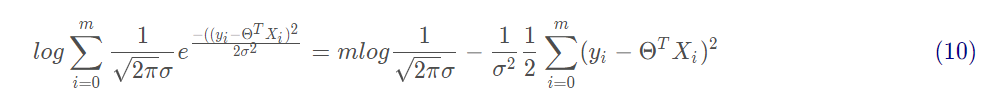
由上式可以看出，右边第一项为一个常量，似然函数要取最大值，因而第二项越小越好，有：

上述公式相当于最小二乘法的式子，即为均方误差的式子。

（2）求解Θ：闭式解。

我们试图让均方误差最小化，即

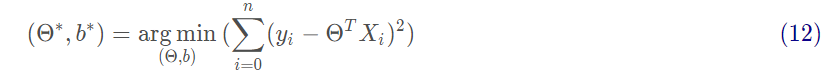
基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧式距离之和最小。求解方法为对Θ求偏导。

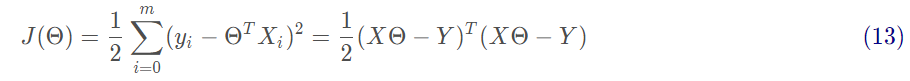
接下来需要对矩阵求偏导，过程如下:

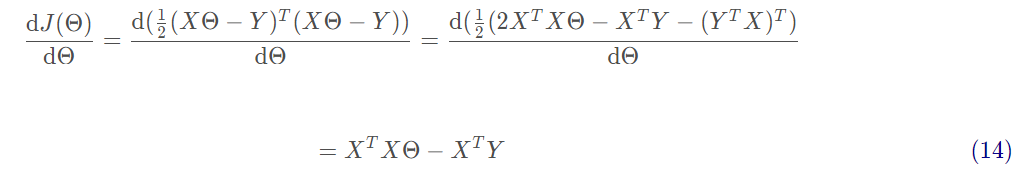
最后令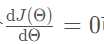可得：

s.t.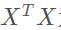为满秩矩阵时。

在现实中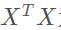往往不是满秩矩阵，在许多变量中会遇到大量的变量，其数目超过样本数目，会导致解出多个Θ，常见的做法是引入正则化或者进行降维。

（3）求解Θ：梯度下降法。

沿着函数梯度方向下降最快的就能找到极小值:

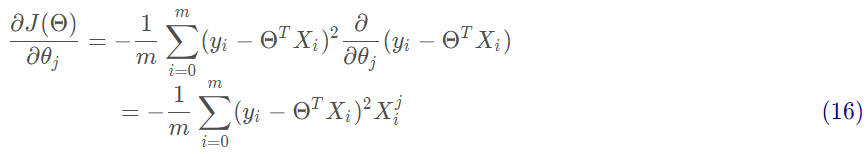
沿着梯度方向更新参数Θ的值:

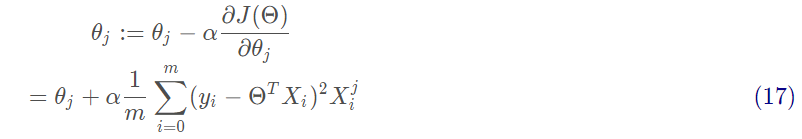
批量梯度下降是用了训练集中的所有样本。因此在数据量很大的时候，每次迭代都要遍历训练集一遍，开销会很大，所以在数据量大的时候，可以采用随机梯度下降法或者批量梯度下降法。

2.2 逻辑回归

对于分类任务，用线性回归无法直接进行回归学习。对于二分类任务，其输出标记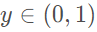，而线性回归模型产生的预测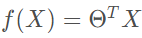值是实值。

2.2.1 对数几率

一个事件的几率是指该事件发生的概率与该事件不发生的概率的比值。p(Y=1|X)是指事件发生的条件概率，p(Y=0|X)是指事件不发生的条件概率，则该事件的对数几率或logit函数是：

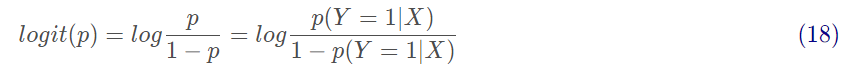
对数几率范围为[0,+∞)，当p=1时候，logit(p)=+∞，当p=0时候，logit(p)=0。

对于逻辑回归而言，有：

将其Θ*X转换为概率有：

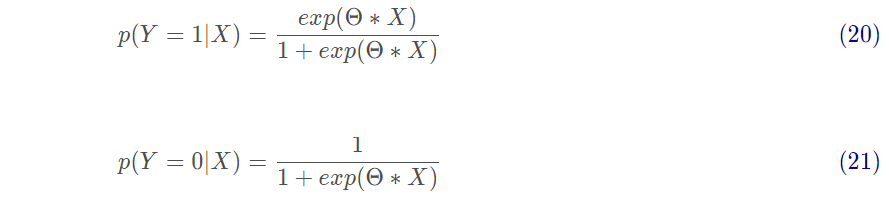
其中

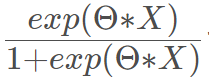
也称为sigmoid函数，函数图如下所示：

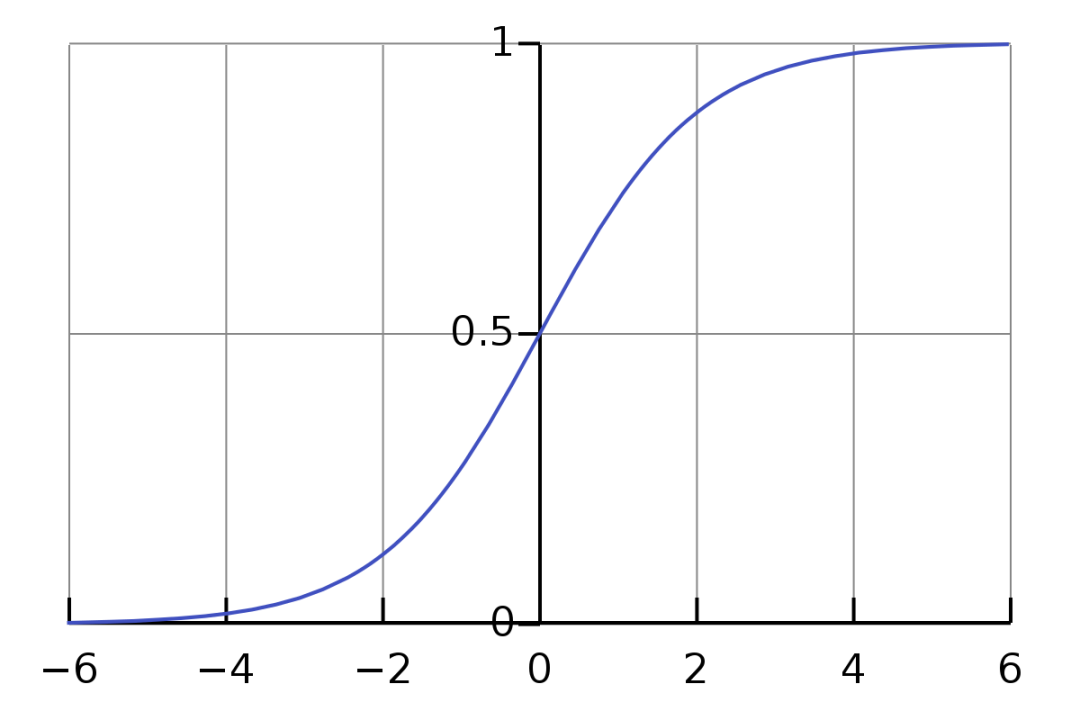
图3 Sigmoid函数图

2.2.2 参数估计

在逻辑回归进行模型学习时，应用极大似然估计来估计模型参数：

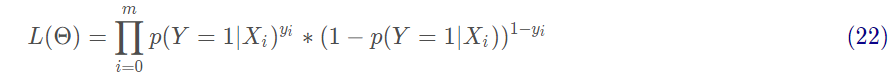
对式22取对数，将连乘转化为加法为：

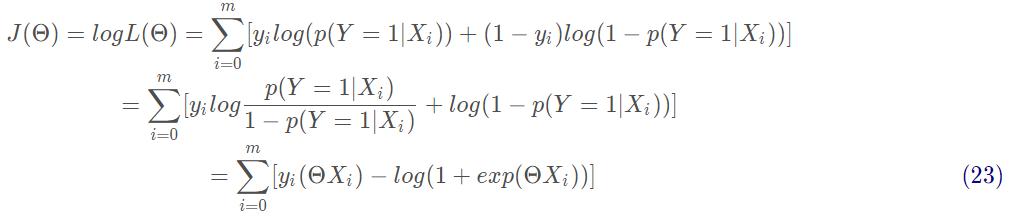
上述公式为求解逻辑回归的损失函数：交叉熵损失函数。

然后对J(Θ)进行求偏导，求最小值，得到Θ的估计值。沿着函数梯度方向下降就能最快的找到极小值:

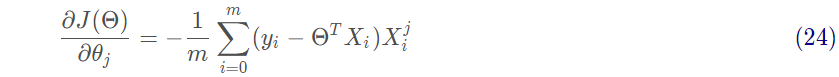
沿着梯度方向更新参数Θ的值:

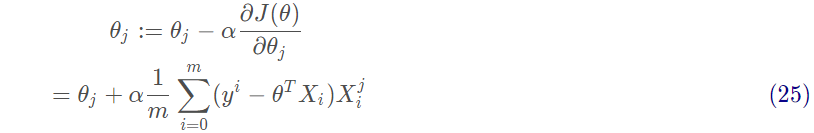
3、实战

3.1 线性回归实战

3.1.1 从零开始实现

1、首先生成数据集

num_inputs = 2 # 数据集的属性 n : 2num_examples = 1000 # 数据集的树木 m : 1000true_w = [2, -3.4]true_b = 4.2 features = torch.randn(num_examples, num_inputs, dtype=torch.float32) # 输入labels = true_w[0]*features[:, 0] + true_w[1]*features[:, 1] + true_b # 标签labels+=torch.tensor(np.random.normal(0,0.01,size=labels.size()),dtype=torch.float32)#加上一些随机噪声

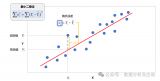
进行可视化后，如下图所示：

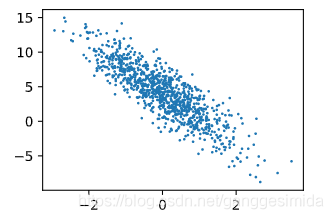
图4 数据集

2、数据读取

def data_iter(batch_size, features, labels): num_examples = len(features) indices = list(range(num_examples)) random.shuffle(indices) for i in range(0, num_examples, batch_size): j = torch.LongTensor(indices[i : min(i + batch_size, num_examples)])yieldfeatures.index_select(0,j),labels.index_select(0,j)

如：当batch_size=10时，我们的输出结果如下所示：

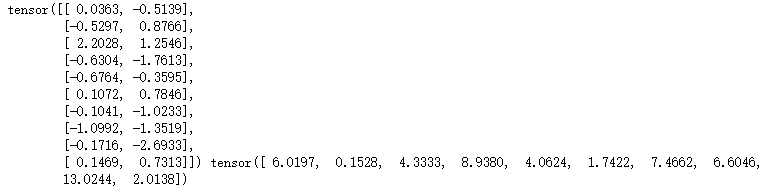
第一个为输入x（size=[10, 2]），第二个为标签y（size=[10]）。

3、定义线性回归模型

def LinReg(X, w, b):returntorch.mm(X,w)+b#torch.mm表示两个矩阵相乘，[batch_size,num_inputs]*[num_inputs,1]=[batch_size,1]

4、定义损失函数

# 线性回归模型的损失函数为均方差损失函数def squared_loss(y_hat, y):return(y_hat-y.view(y_hat.size()))**2/2

5、定义优化算法

# 这里我们使用梯度下降算法：sdgdef sgd(params, lr, batch_size): for param in params:param.data-=lr*param.grad/batch_size

6、进行训练

训练步骤如下：

（1）首先读取一个batch_size的数据和标签
（2）然后进行模型计算；
（3）然后计算损失函数；
（4）然后反向求导优化参数；

lr = 0.03num_epochs = 3net = LinRegloss = squared_loss for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期 # 在每一个迭代周期中，会使用训练数据集中所有样本一次（假设样本数能够被批量大小整除）。X # 和y分别是小批量样本的特征和标签 for X, y in data_iter(batch_size, features, labels): l = loss(net(X, w, b), y).sum() # l是有关小批量X和y的损失 l.backward() # 小批量的损失对模型参数求梯度 sgd([w, b], lr, batch_size) # 使用小批量随机梯度下降迭代模型参数 # 不要忘了梯度清零 w.grad.data.zero_() b.grad.data.zero_() train_l = loss(net(features, w, b), labels)print('epoch%d,loss%f'%(epoch+1,train_l.mean().item()))

最后输出结果如下所示：

epoch 1, loss 0.044750epoch 2, loss 0.000172epoch3,loss0.000049

3.2 逻辑回归实战

逻辑回归相比线性回归中，改变的地方为第3步：模型函数 和 第4步：损失函数。

3.2.1 从零实现逻辑回归

3、定义逻辑回归模型

def sigmoid(X, w, b): ''' 定义sigmoid函数 :param x: 参数x 返回计算后的值 ''' z = torch.mm(X, w) + breturn1.0/(1+np.exp(-z))

4、定义损失函数

# 在逻辑回归中，我们使用的是对数损失函数（交叉熵损失函数）def BCE_loss(y_hat, y): ''' 损失函数 :param y_hat: 预测值 :param y: 实际值 loss ''' m = np.shape(y_hat)[0] loss = 0.0 for i in range(m): if y_hat[i, 0] > 0 and (1 - y_hat[i, 0]) > 0: loss-= (y[i, 0] * np.log(y_hat[i, 0]) + (1 - y[i, 0]) * np.log(1 - y_hat[i, 0])) else: loss-= 0.0returnloss/m

责任编辑：xj

原文标题：【机器学习】线性回归与逻辑回归的理论与实战

文章出处：【微信公众号：深度学习自然语言处理】欢迎添加关注！文章转载请注明出处。