我一直有一个感觉:咱们硬件工程师,会遇到各种各样的问题,亦或是各种各样的现象,总会有一个非常简单的解释,一句话或者是几句话,我们见多了这个解释,就自以为明白了,当别人再问起我们的时候,我们也会拿这句话去给别人解释。
比如说,寄生电感这个字眼就经常出现,特别是引线电感。我们解释一些问题的时候都是直接套用的,默认它的存在。可实际上是,我在很长一段时间内并不理解它到底是怎么来的,因为我印象中电感都是线圈,而直导线并不是。直到之前不久我才思索了一番,算是有一些了解,也写了下面一篇文章。
寄生电感怎么来的
最近一直在看电感和磁珠的内容,也有看LC滤波器,自然会有LC谐振的问题。LC串联谐振,单独拿出来说的话,可能会觉得太简单了,这有啥好说的。自然是因为实际应用中会出现各种各样的场景,尽管都是谐振,但是表现各不相同。
先来思考下这么几个问题:
电路中不必要的LC串联谐振要绝对杜绝吗?
MOS管G极经常串联一个小电阻,说是可以抑制振荡,啥原理呢?这个电阻阻值怎么取呢?
电源上面加上磁珠,结果纹波变大了,只能换0Ω电阻来解决吗?有没有其它的解决方法?
这几个问题,如果你明白了LC串联谐振的分析方法,那么自然都不在话下了。
LC串联谐振电路
尽管LC串联谐振电路非常简单,我们还是来看下,这样一步一步深入会更好的理解。
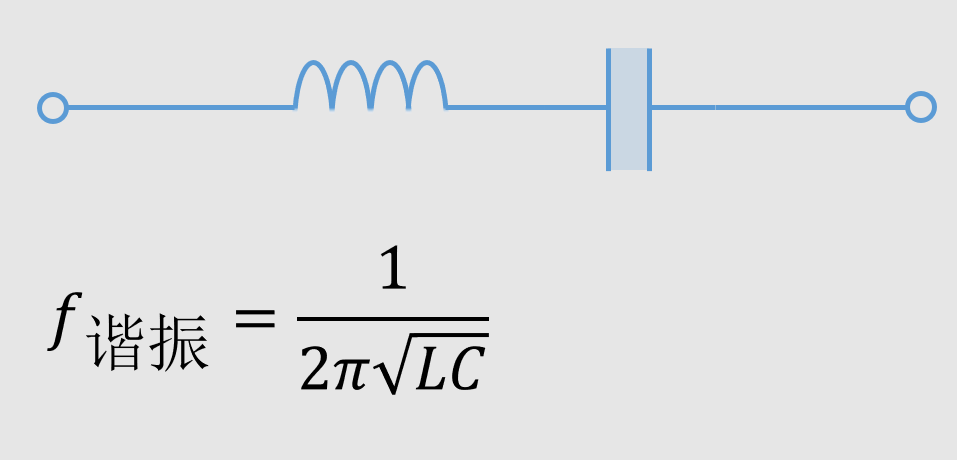
一个电感和一个电容串联,在某个特定的频率,就会发生谐振,这个频率就是谐振频率。串联谐振电路有如下特点:
谐振时整个电路阻抗呈电阻性,阻抗最小,电流达到最大;
谐振时电感和电容两端的电压达到最大。
上面这些理论都是非常基础的,就不赘述。实际电路的场景要远比这个要复杂,搞清楚那些才是我们的目的。那么我们下面就来结合具体的场景。
LC滤波器
LC滤波器经常用,但有一个比较坑的问题就是,有时候使用LC滤波器之后,效果反而更差了,还不如不用。
原因我们当然可以说是在噪声在此处谐振啦,噪声被放大了之类的。曾经的我也会这么说原因,不过并不是真的明白,对于这种会起反效果的东西,我会惧怕,会担心它出问题。这种惧怕,来源于对未知的恐惧,因为没有懂。现在下面来具体分析下
首先,我们需要明白,噪声是如何被放大的?也就是说输出比输入幅度要大?
先来看最简单的模型,也就是理想器件模型的情况。
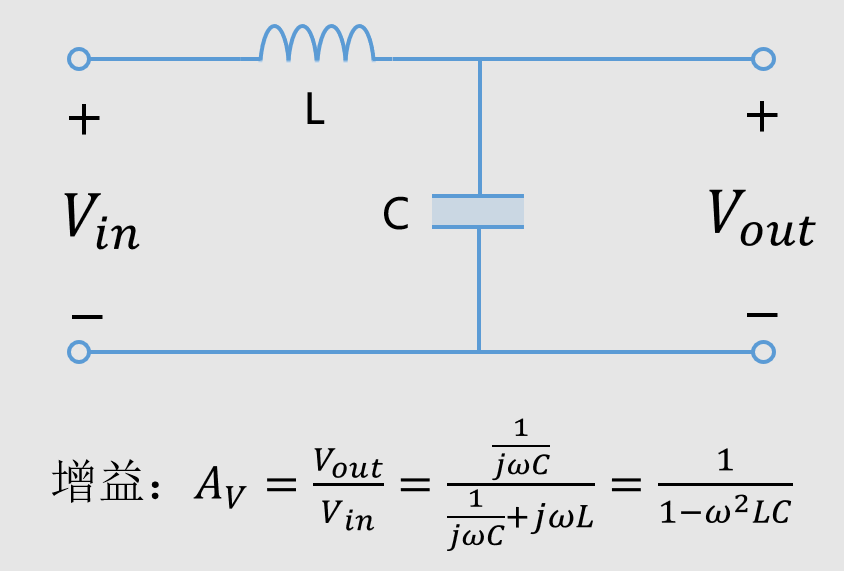
我们列出输出与输入的比值,也就是增益,如果增益大于1,那么说明被放大了。很容易列出增益的公式,我们画下这个曲线。
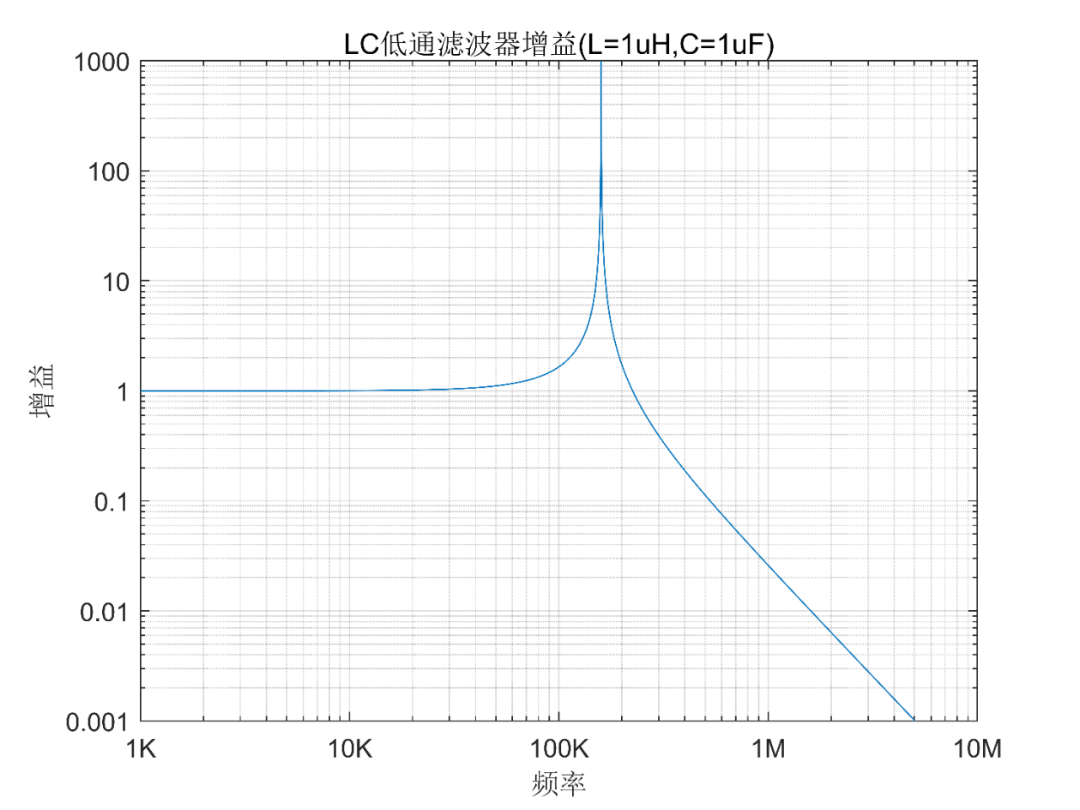
上图的曲线,是1uH电感,1uF电容的增益。可以看到,在低频时,增益基本就是1,也就是不放大不衰减。而在谐振频率处,有一个非常高的尖峰,因为这里设定的器件为理想器件,所理论上尖峰为穷大,谐振频率旁边的增益也是非常高的,而在频率比较高的时候,随着频率的升高,增益下降,也就是衰减了输入信号。
如果我们能把谐振频率处的增益降到0.707左右,那就是完美的低通滤波器了。很显然,电感和电容都是非耗能器件,没有电阻器件的引入,在谐振频率处,增益总是等于无穷大的。我们从增益Av的公式就可以得出来,因为谐振频率时的分母为0。
幸运的是,我们的滤波电路总是要接负载的,我们把信号滤波之后总是要给负载用的,接入了负载,那增益又不一样了。
不同负载的LC滤波器
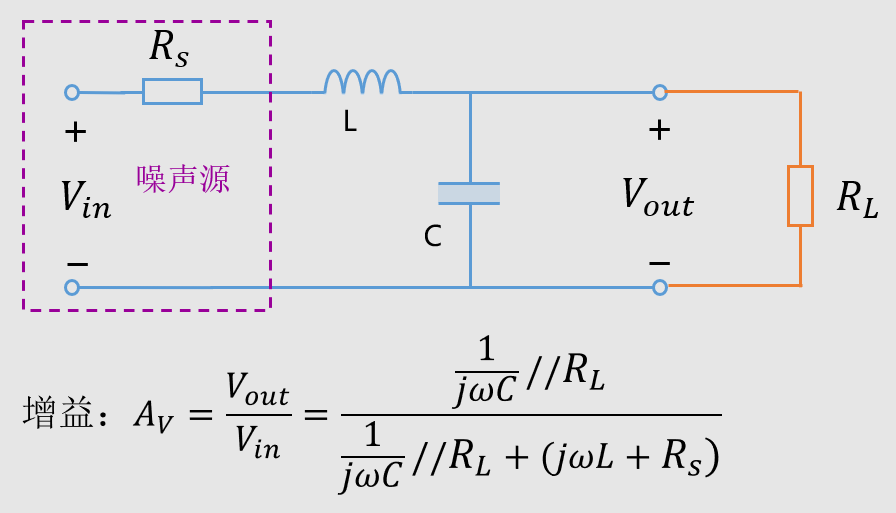
现实中的电路各种各样,负载的阻抗也就差别很大了,下面是加入负载的模型。
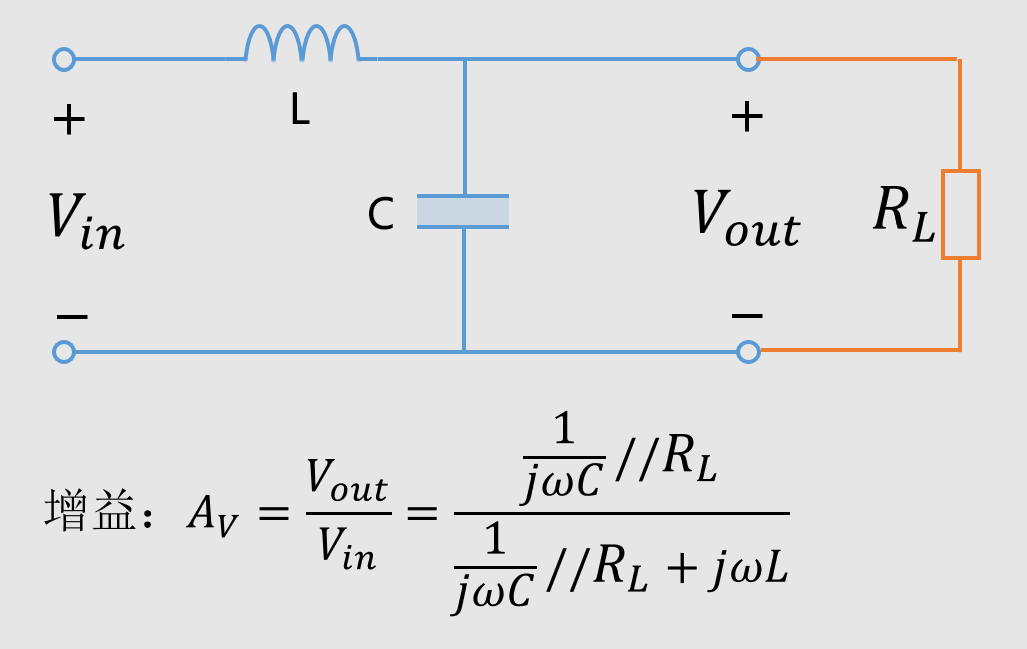
我们看看负载是1Ω,10Ω,100Ω的增益曲线,如下图:
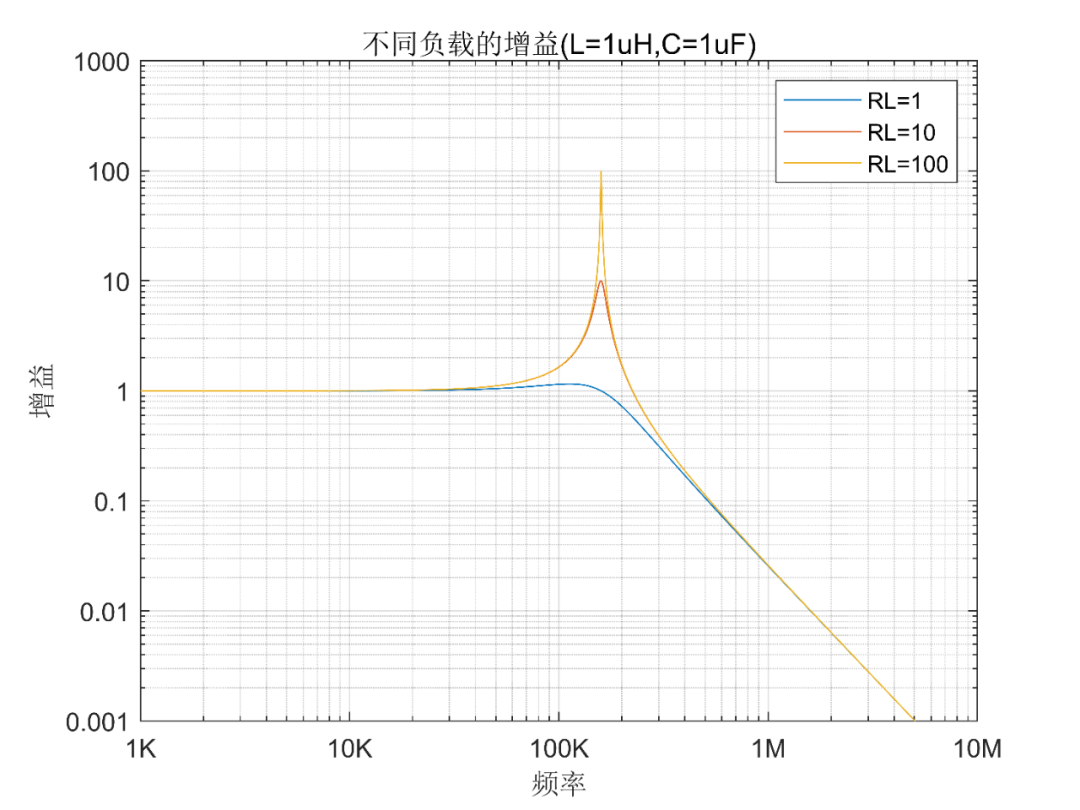
我们可以看到,负载电阻越小,谐振处的增益越小,谐振引起的噪声变大越不会发生。当然了,实际电路中的负载各种各样,有低阻的,有高阻的。相对来说,低阻负载的更不容易发生加入滤波器效果更差的事情。因此,如果你发现同样的LC滤波器,加入不同的电路,有的效果好,有的效果变差,很有可能就是因为负载的不同。
所以说,负载阻抗越低,越不容易产生尖峰,也就是说不容易恶化。
噪声源内阻的影响
除了负载阻抗的影响,还有噪声源内阻的影响,实际的噪声信号肯定是有一定的内阻的。根据内阻的不同,我们构建下面的模型,加入内阻的参量。
分别画出Rs=0.1Ω,Rs=1Ω,Rs=10Ω的情况,为了排除负载电阻的影响,宁其为高阻态,统一RL=1MΩ。
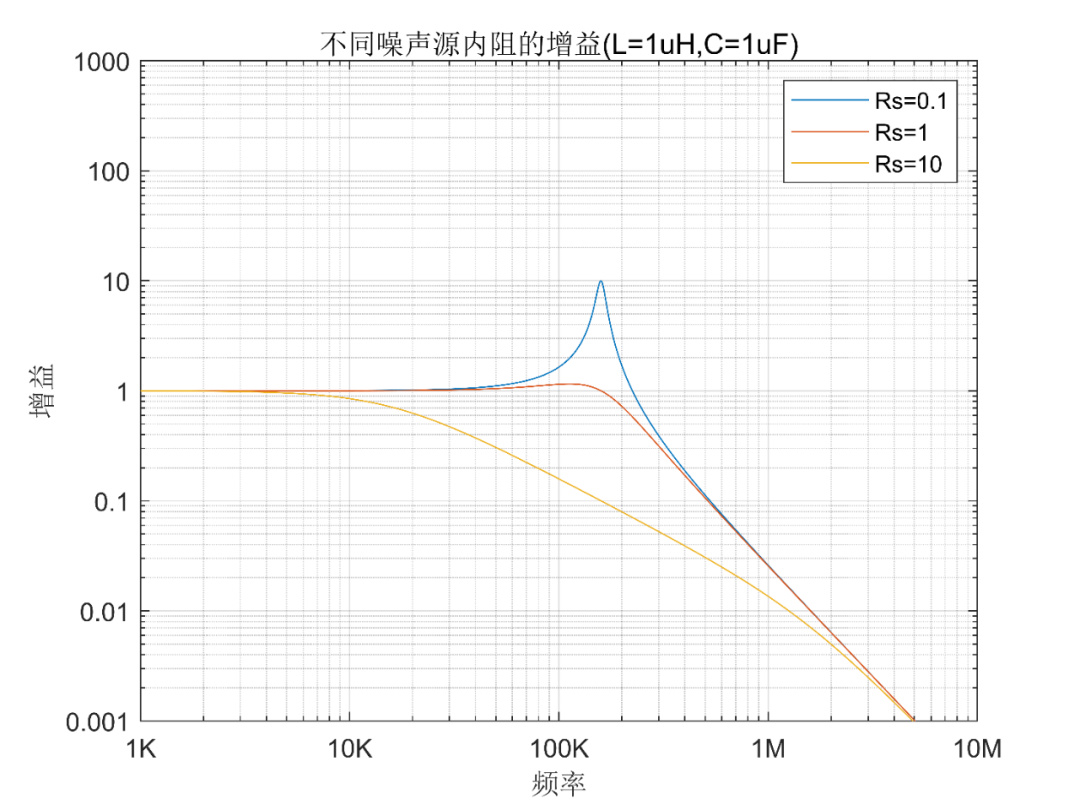
可以看到,内阻越大,越不容易产生尖峰,也就是说不容易恶化,反之,内阻越小,越容易恶化。
L、C的值的影响
除了内阻和负载大小,电感和电容值的大小有没有影响呢?
电容变化:电容分别为1uF,10uF,100uF,内阻,负载,电感都为Rs=0.1,RL=1MΩ,L=1uH。
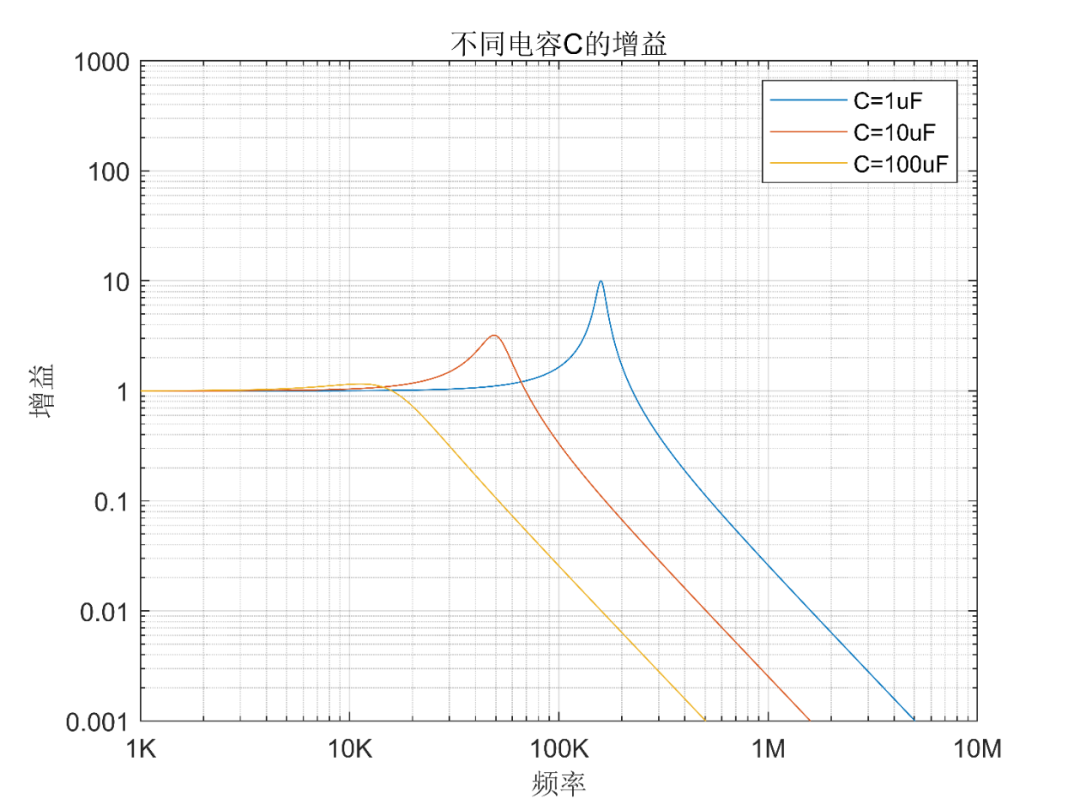
可以看到,电容增大,尖峰变小,也就是说,在遇到谐振引起噪声增大的情况,可以尝试增大电容是可以降低噪声。不过需要注意,尖峰变小,只是说最高点变小了,但是引起了谐振频率降低,新的谐振点可能还是要比原来的增益更高,也就是说如果噪声正好是这个频率段,那么改变之后效果变更差了。当然了,如果我们加更大的电容,即使是谐振点都没有放大作用,比如如果电容加到100uF,整个频段基本都没有放大作用了。
实际电路具体加到多大的电容,完全不会出现尖峰呢?这个跟信号源内阻Rs,负载阻抗RL,电感值L都有关系。实际上,如果内阻Rs从0.1提升到1,电容不用增大到100uF,即使是原来的1uf也不会有尖峰,曲线就不画了。
电感变化:电感分别为0.01uH,0.1uH,1uH,内阻,负载,电容都为Rs=0.1,RL=1MΩ,C=1uF
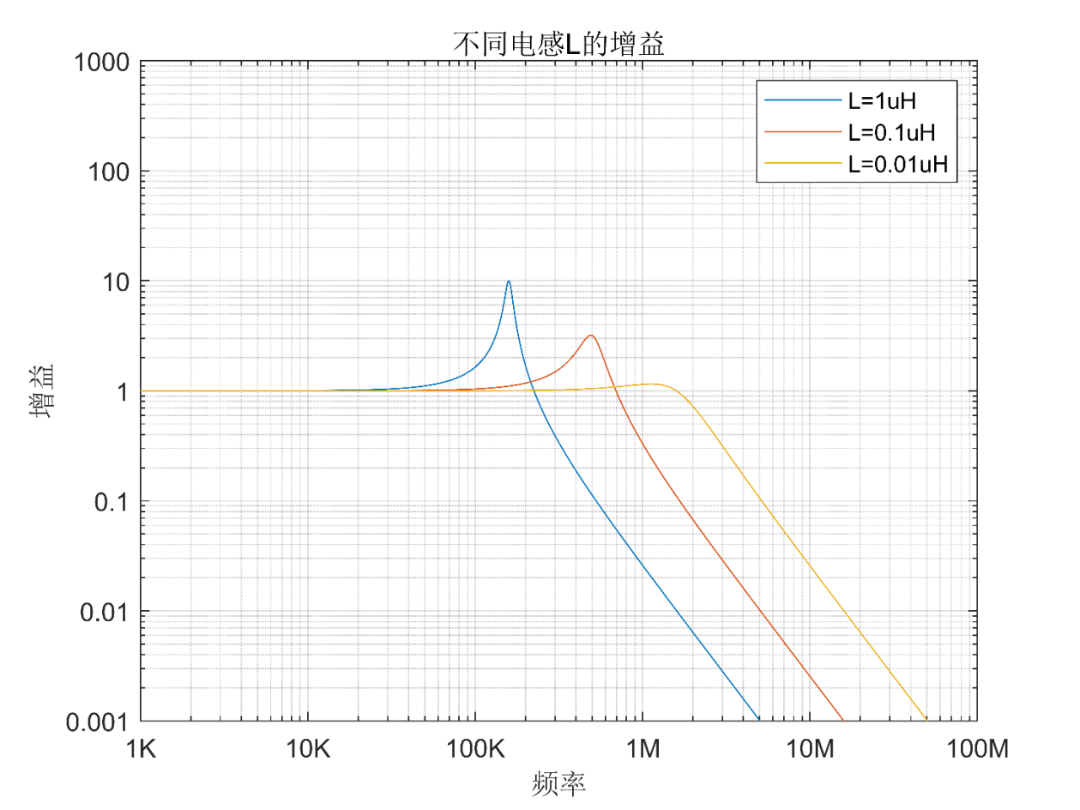
可以看到,减小电感,可以降低尖峰的高度。我们如果继续减小电感到0.01uH,尖峰也会消失。同样的,电感变化会造成谐振频率移动,具体是使噪声变大还是变小也是要依情况而定,与内阻,负载,电容都有关系。
总的来说,大部分电路增大电容,或者减小电感,都可以降低尖峰。如果LC滤波器用于电源滤波发生噪声变大,可以增大电容,或者减少电感。
这里之所以说大部分电路,是因为如果满足一定的Rs,RL的条件,可能结果是相反的,这个可以自己修改Matlab代码(后文分享出来)里面的参量,执行下就知道了。
MOS管G极串联电阻如何抑制谐振
有了以上的基础,我们来看实际的问题:MOS管G极串联电阻如何抑制谐振?
这个问题,我们首先要明白,问题是如何产生的,即为什么会振荡?其实通过前面的铺垫,也就很明白了。
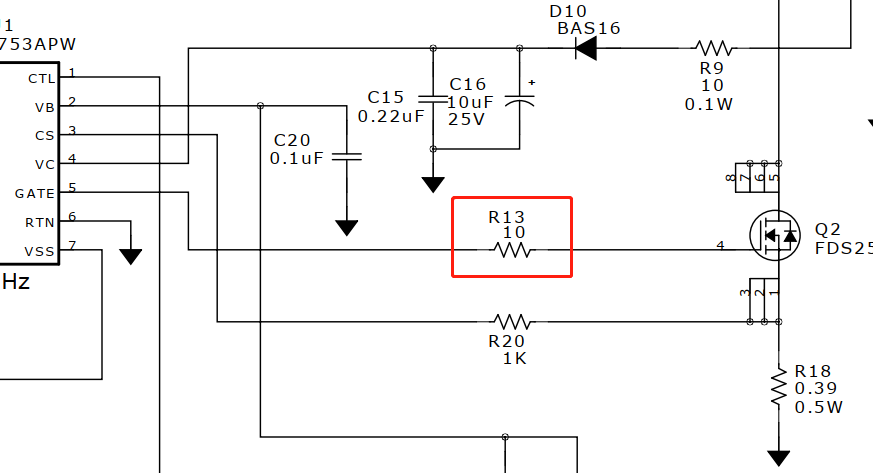
这个是典型的MOS管驱动电路,串联了10Ω电阻。
尽管从电路图上看去,上面既没有电感,也没有电容。但实际上是,我们PCB总要将线从驱动芯片拉到MOS管,我查了一下,线宽12mil,长度10mm的走线寄生电感是9.17nH。实际电路中10mm走线太正常了,所以寄生电感肯定是存在的。
电感有了,电容呢?功率MOS管都有输入电容存在,并且还不小,小的几百pF,大点的几nF。我们只是为了说明道理,那取电容1nF吧。
一般来说,左边驱动管子发出开关信号,它的内阻一般不会很低,尽管现在不知道它到底是多大,那就按照比较恶劣的情况来看,就让Rs=0.1Ω。
那么负载电阻是多大呢?负载是MOS管,那阻抗就很大了,就取RL=1MΩ。
看看现在的等效电路:
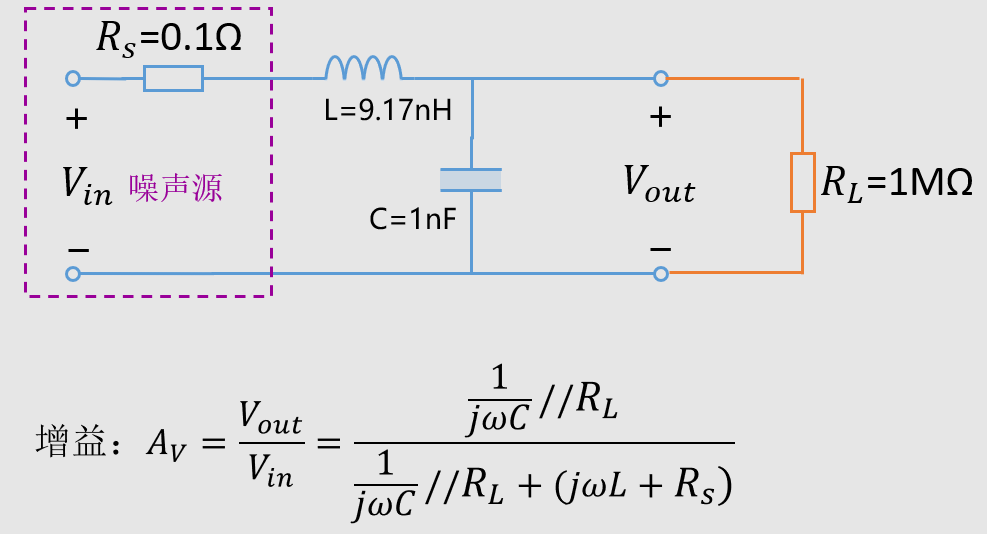
从前面内容知道,源内阻越小,负载阻抗越大,就越容易产生谐振尖峰。我们画出此时曲线。
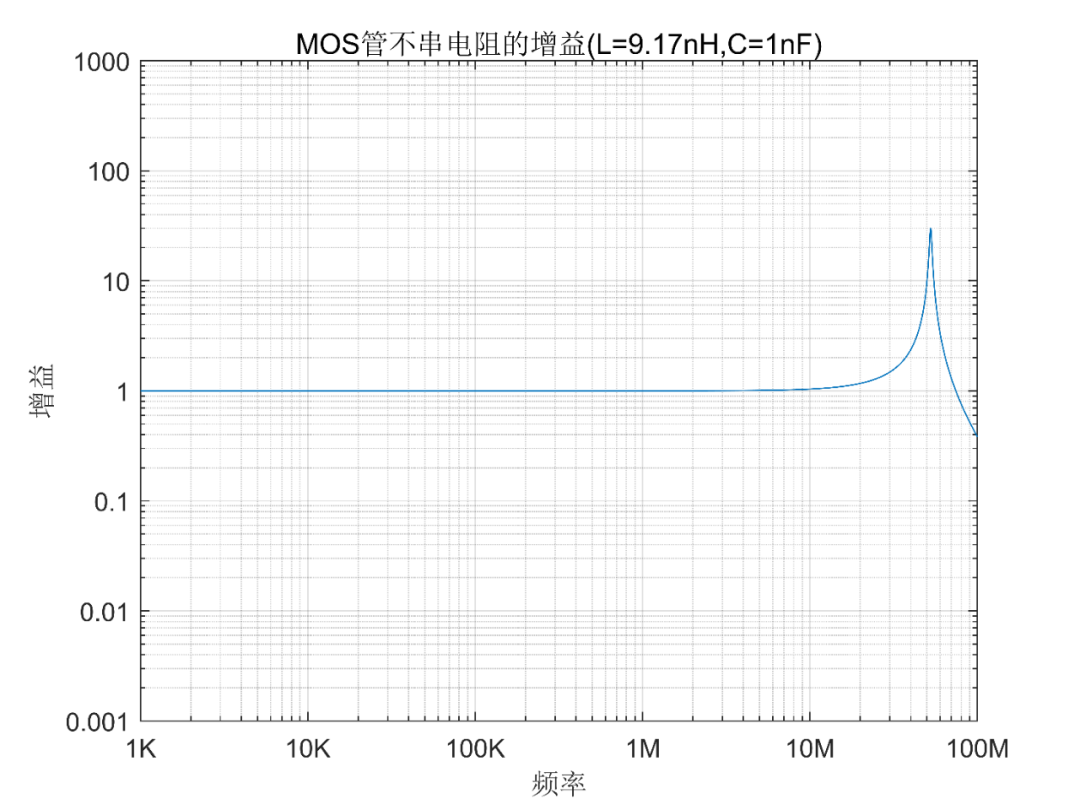
可以看到,谐振频率52Mhz处增益达到了好几十倍。而MOS管驱动信号可以看作是一个阶跃信号,频率分量非常丰富,肯定有52Mhz附近的频率。
所以说确实会发生谐振。
现在分别串联1Ω,10Ω,100Ω电阻,这个电阻可以等效到内阻里面去,相当于等效电路变成了Rs=1.1Ω,Rs=10.1Ω,Rs=100.1Ω,其它参数不变。我们再看看曲线。
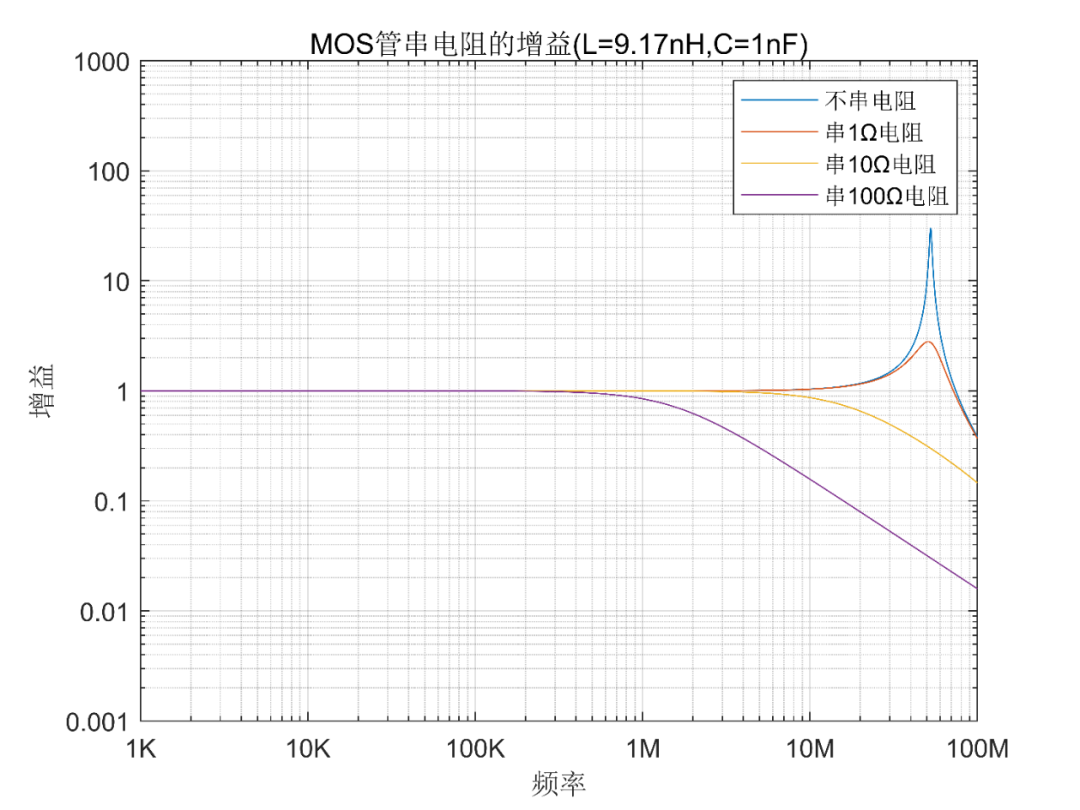
可以看到,串联1Ω电阻,还是放大,最大到3倍,说明电阻稍小。而10Ω电阻就能完全消除振荡了。100Ω电阻也能完全消除振荡,但是其截止频率更低,会造成驱动信号的高频分量丢失,最终上升沿变缓,也就是MOS管开启的时间变长。
相信到这里,对于这个串联电阻的作用,已经怎么取值应该就比较清楚了。G极走线越长,寄生电感越大,越容易引起问题,电阻就要选得更大些。
从文章开头,一路看下来,这也太费劲了,确实,明白这些也不是很容易,很多时候,我们都是拿着厂家的原理图来抄抄,也不会有问题。等到有新人问到“这个电阻干什么用的?”老员工答曰“抑制振荡”,是啊,这四个字,每个字都认识,是不是总有一种模模糊糊的感觉呢?希望看完此文之后不再模糊。
Matlab源码
上面所有的曲线图,Matlab源码都在这个里面了,我已经把每个图对应的代码分开来了,有7部分,全部复制过去可以一次执行得到7个图。也可以把其中的一个复制出去执行,都是可以的。代码里面的注释写得也比较清楚,可以自行去修改Rs,RL,L,C的值
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%---理想LC低通滤波器增益
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
f=[1000:100:100000000]; %频率:范围1Khz-10Mhz
w=(f.*pi*2); %角频率
C=0.000001; %1uF 电容量
L=0.000001; %1uH 电感量
Zc=1./(w.*C.*j); %电容总阻抗
Zl=w.*L.*j; %电感总阻抗
Av= abs(Zc./(Zc+Zl)); %增益
figure; %画图
loglog(f,Av); %画出增益曲线
grid on; %显示网格
set(gca,‘YLim’,[0.001 1000]);%y轴的数据显示范围
set(gca, ‘XTickLabel’ ,{‘1K’,‘10K’,‘100K’,‘1M’,‘10M’,‘100M’}); %x轴频率数据
set(gca, ‘YTickLabel’ ,{‘0.001’,‘0.01’,‘0.1’,‘1’,‘10’,‘100’,‘1000’}); %y轴幅度数据
xlabel(‘频率’), ylabel(‘增益’); %x,y轴名称
title([‘LC低通滤波器增益(L=’,num2str(L*1000000),‘uH,C=’,num2str(C*1000000),‘uF)’]);%标题
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%---不同负载
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
f=[1000:100:100000000]; %频率:范围1Khz-10Mhz
w=(f.*pi*2); %角频率
C=0.000001; %1uF 电容量
L=0.000001; %1uH 电感量
RL1=1; %负载RL1=1
RL2=10; %负载RL2=10
RL3=100; %负载RL2=100
Zc=1./(w.*C.*j); %电容总阻抗
Zl=w.*L.*j; %电感总阻抗
Av1=abs(((Zc.*RL1)。/(Zc+RL1))。/(((Zc.*RL1)。/(Zc+RL1))+Zl)); %负载1对应增益
Av2=abs(((Zc.*RL2)。/(Zc+RL2))。/(((Zc.*RL2)。/(Zc+RL2))+Zl)); %负载2对应增益
Av3=abs(((Zc.*RL3)。/(Zc+RL3))。/(((Zc.*RL3)。/(Zc+RL3))+Zl)); %负载3对应增益
figure; %画图
loglog(f,Av1,f,Av2,f,Av3); %画出3种负载的增益
grid on; %显示网格
legend([‘RL=’,num2str(RL1)],[‘RL=’,num2str(RL2)],[‘RL=’,num2str(RL3)]);%曲线说明
set(gca,‘YLim’,[0.001 1000]);%y轴的数据显示范围
set(gca, ‘XTickLabel’ ,{‘1K’,‘10K’,‘100K’,‘1M’,‘10M’,‘100M’}); %x轴频率数据
set(gca, ‘YTickLabel’ ,{‘0.001’,‘0.01’,‘0.1’,‘1’,‘10’,‘100’,‘1000’}); %y轴幅度数据
xlabel(‘频率’), ylabel(‘增益’); %x,y轴名称
title([‘不同负载的增益(L=’,num2str(L*1000000),‘uH,C=’,num2str(C*1000000),‘uF)’]);%标题
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%---不同噪声源内阻
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
f=[1000:100:100000000]; %频率:范围1Khz-10Mhz
w=(f.*pi*2); %角频率
C=0.000001; %1uF 电容量
L=0.000001; %1uH 电感量
RS1=0.1; %内阻RS1=0.1
RS2=1; %内阻RS2=1
RS3=10; %内阻RS2=10
RL=1000000;%负载RL=1
MZc=1./(w.*C.*j); %电容总阻抗
Zl=w.*L.*j; %电感总阻抗
Av1=abs(((Zc.*RL)。/(Zc+RL))。/(((Zc.*RL)。/(Zc+RL))+Zl+RS1)); %内阻1对应增益
Av2=abs(((Zc.*RL)。/(Zc+RL))。/(((Zc.*RL)。/(Zc+RL))+Zl+RS2)); %内阻2对应增益
Av3=abs(((Zc.*RL)。/(Zc+RL))。/(((Zc.*RL)。/(Zc+RL))+Zl+RS3)); %内阻3对应增益
figure; %画图
loglog(f,Av1,f,Av2,f,Av3); %画出3种内阻的增益
grid on; %显示网格
legend([‘Rs=’,num2str(RS1)],[‘Rs=’,num2str(RS2)],[‘Rs=’,num2str(RS3)]);%曲线说明
set(gca,‘YLim’,[0.001 1000]);%y轴的数据显示范围
set(gca, ‘XTickLabel’ ,{‘1K’,‘10K’,‘100K’,‘1M’,‘10M’,‘100M’}); %x轴频率数据
set(gca, ‘YTickLabel’ ,{‘0.001’,‘0.01’,‘0.1’,‘1’,‘10’,‘100’,‘1000’}); %y轴幅度数据xlabel(‘频率’), ylabel(‘增益’); %x,y轴名称
title([‘不同噪声源内阻的增益(L=’,num2str(L*1000000),‘uH,C=’,num2str(C*1000000),‘uF)’]);%标题
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%---不同的电容C的值
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
f=[1000:100:100000000]; %频率:范围1Khz-10Mhz
w=(f.*pi*2); %角频率
C1=0.000001; %1uF 电容量1
C2=0.00001; %10uF 电容量2
C3=0.0001; %100uF 电容量3
L=0.000001; %1uH 电感量RS=0.1; %内阻RS1=0.1
RL=1000000;%负载RL=1M
Zc1=1./(w.*C1.*j); %电容C1总阻抗
Zc2=1./(w.*C2.*j); %电容C2总阻抗
Zc3=1./(w.*C3.*j); %电容C3总阻抗
Zl=w.*L.*j; %电感总阻抗
Av1= abs(((Zc1.*RL)。/(Zc1+RL))。/(((Zc1.*RL)。/(Zc1+RL))+Zl+RS));%电容1对应增益
Av2= abs(((Zc2.*RL)。/(Zc2+RL))。/(((Zc2.*RL)。/(Zc2+RL))+Zl+RS));%电容2对应增益
Av3= abs(((Zc3.*RL)。/(Zc3+RL))。/(((Zc3.*RL)。/(Zc3+RL))+Zl+RS));%电容2对应增益
figure; %画图
loglog(f,Av1,f,Av2,f,Av3); %画出3种电容的增益
grid on; %显示网格
legend([‘C=’,num2str(C1*1000000),‘uF’],[‘C=’,num2str(C2*1000000),‘uF’],[‘C=’,num2str(C3*1000000),‘uF’]);%曲线说明
set(gca,‘YLim’,[0.001 1000]);%y轴的数据显示范围set(gca, ‘XTickLabel’ ,{‘1K’,‘10K’,‘100K’,‘1M’,‘10M’,‘100M’}); %x轴频率数据
set(gca, ‘YTickLabel’ ,{‘0.001’,‘0.01’,‘0.1’,‘1’,‘10’,‘100’,‘1000’}); %y轴幅度数据xlabel(‘频率’), ylabel(‘增益’); %x,y轴名称
title([‘不同电容C的增益’]);%标题
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%---不同的电感L的值
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
f=[1000:100:100000000]; %频率:范围1Khz-10Mhz
w=(f.*pi*2); %角频率
C=0.000001; %1uF 电容量
L1=0.000001; %1uH 电感量
L2=0.0000001; %0.1uH 电感量
L3=0.00000001; %0.01uH 电感量
RS=0.1; %内阻RS1=0.1
RL=1000000;%负载RL=1M
Zc=1./(w.*C.*j); %电容C总阻抗
Zl1=w.*L1.*j; %电感L1总阻抗
Zl2=w.*L2.*j; %电感L2总阻抗
Zl3=w.*L3.*j; %电感L3总阻抗
Av1= abs(((Zc.*RL)。/(Zc+RL))。/(((Zc.*RL)。/(Zc+RL))+Zl1+RS));%电感1对应增益
Av2= abs(((Zc.*RL)。/(Zc+RL))。/(((Zc.*RL)。/(Zc+RL))+Zl2+RS));%电感2对应增益
Av3= abs(((Zc.*RL)。/(Zc+RL))。/(((Zc.*RL)。/(Zc+RL))+Zl3+RS));%电感3对应增益
figure; %画图
loglog(f,Av1,f,Av2,f,Av3); %画出3种电感的增益
grid on; %显示网格
legend([‘L=’,num2str(L1*1000000),‘uH’],[‘L=’,num2str(L2*1000000),‘uH’],[‘L=’,num2str(L3*1000000),‘uH’]);%曲线说明
set(gca,‘YLim’,[0.001 1000]);%y轴的数据显示范围
set(gca, ‘XTickLabel’ ,{‘1K’,‘10K’,‘100K’,‘1M’,‘10M’,‘100M’}); %x轴频率数据
set(gca, ‘YTickLabel’ ,{‘0.001’,‘0.01’,‘0.1’,‘1’,‘10’,‘100’,‘1000’}); %x轴幅度数据
xlabel(‘频率’), ylabel(‘增益’); %x,y轴名称
title([‘不同电感L的增益’]);%标题
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%---MOS不串电阻
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
f=[1000:100:100000000]; %频率:范围1Khz-10Mhz
w=(f.*pi*2); %角频率
C=0.000000001; %1nF 电容量
L=0.00000000917; %1uH 电感量
RS=0.1; %内阻RS1=0.1
RL=1000000;%负载RL=1M
Zc=1./(w.*C.*j); %电容总阻抗
Zl=w.*L.*j; %电感总阻抗
Av=abs(((Zc.*RL)。/(Zc+RL))。/(((Zc.*RL)。/(Zc+RL))+Zl+RS)); %MOS管不串增益
figure; %画图
loglog(f,Av); %画出增益曲线
grid on; %显示网格
set(gca,‘YLim’,[0.001 1000]);%y轴的数据显示范围
set(gca, ‘XTickLabel’ ,{‘1K’,‘10K’,‘100K’,‘1M’,‘10M’,‘100M’}); %x轴频率数据
set(gca, ‘YTickLabel’ ,{‘0.001’,‘0.01’,‘0.1’,‘1’,‘10’,‘100’,‘1000’}); %x轴幅度数据
xlabel(‘频率’), ylabel(‘增益’); %x,y轴名称
title([‘MOS管不串电阻的增益(L=’,num2str(L*1000000000),‘nH,C=’,num2str(C*1000000000),‘nF)’]);%标题
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%---MOS串电阻
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
f=[1000:100:100000000]; %频率:范围1Khz-10Mhz
w=(f.*pi*2); %角频率
C=0.000000001; %1nF 电容量
L=0.00000000917; %1uH 电感量
RS1=0.1; %内阻RS1=0.1
RS2=1.1; %内阻RS1=1.1
RS3=10.1; %内阻RS1=10.1
RS4=100.1; %内阻RS1=100.1
RL=1000000;%负载RL=1M
Zc=1./(w.*C.*j); %电容总阻抗
Zl=w.*L.*j; %电感总阻抗
Av1=abs(((Zc.*RL)。/(Zc+RL))。/(((Zc.*RL)。/(Zc+RL))+Zl+RS1)); %MOS管不串增益
Av2=abs(((Zc.*RL)。/(Zc+RL))。/(((Zc.*RL)。/(Zc+RL))+Zl+RS2)); %MOS管串1Ω电阻增益
Av3=abs(((Zc.*RL)。/(Zc+RL))。/(((Zc.*RL)。/(Zc+RL))+Zl+RS3)); %MOS管串1Ω电阻增益
Av4=abs(((Zc.*RL)。/(Zc+RL))。/(((Zc.*RL)。/(Zc+RL))+Zl+RS4)); %MOS管串1Ω电阻增益
figure; %画图
loglog(f,Av1,f,Av2,f,Av3,f,Av4); %画出增益曲线
grid on; %显示网格
legend([‘不串电阻’],[‘串1Ω电阻’],[‘串10Ω电阻’],[‘串100Ω电阻’]);%曲线说明
set(gca,‘YLim’,[0.001 1000]);%y轴的数据显示范围
set(gca, ‘XTickLabel’ ,{‘1K’,‘10K’,‘100K’,‘1M’,‘10M’,‘100M’}); %x轴频率数据
set(gca, ‘YTickLabel’ ,{‘0.001’,‘0.01’,‘0.1’,‘1’,‘10’,‘100’,‘1000’}); %x轴幅度数据
xlabel(‘频率’), ylabel(‘增益’); %x,y轴名称title([‘MOS管串电阻的增益(L=’,num2str(L*1000000000),‘nH,C=’,num2str(C*1000000000),‘nF)’]);%标题
小结
LC串联电路非常简单,然而实际电路应用起来却不简单,从而会引起各种各样的现象,如果不深入分析的话,确实会有点无从下手。下面写几个小结论:
1、LC串联谐振的增益,与信源内阻,负载阻抗,电感,电容的大小都有很大的关系,四个变量造成的情景组合非常多,表现也就有很不一样。总的来说信源内阻越小,负载阻抗越大,电感越大,电容越小,越容易出现尖峰
2、LC滤波器恶化要满足几个条件:源内阻要小,负载阻抗要大,噪声频率正好处于谐振频率附近,电容容量太小,电感感量太大。
这些结论,个人认为真心不重要,重要的是分析方法。有了方法,各种结论不是随便就推出来了,还用别人告诉你吗?至于开篇提的几个问题,自然答案就出来了。
责任编辑:xj
-
CMOS
+关注
关注
58文章
5750浏览量
236282 -
串联电路
+关注
关注
6文章
160浏览量
25784 -
硬件工程师
+关注
关注
188文章
361浏览量
75980
发布评论请先 登录
相关推荐
串联谐振和并联谐振特性对比及介绍
串联谐振和并联谐振的特点区别
什么是串联谐振,为什么会发生串联谐振?
串联谐振回路和并联谐振回路的特性是什么
串联谐振回路与并联谐振回路的比较
调感串联谐振装置操作方法
串联谐振和并联谐振各有什么特点
【技术课堂】拓扑篇丨LC串联谐振拓扑仿真建模及控制策略分析
LC串联谐振拓扑仿真建模及控制策略分析





 LC串联谐振的分析方法
LC串联谐振的分析方法











评论