1.分辩率(Resolution) 指数字量变化一个最小量时模拟信号的变化量,定义为满刻度与2n的比值。分辩率又称精度,通常以数字信号的位数来表示。
2.转换速率(Conversion Rate)是指完成一次从模拟转换到数字的AD转换所需的时间的倒数。
积分型AD的转换时间是毫秒级属低速AD,逐次比较型AD是微秒级属中速AD,全并行/串并行型AD可达到纳秒级。采样时间则是另外一个概念,是指两次转换的间隔。为了保证转换的正确完成,采样速率(Sample Rate)必须小于或等于转换速率。因此有人习惯上将转换速率在数值上等同于采样速率也是可以接受的。常用单位是ksps 和Msps,表示每秒采样千/百万次(kilo/Million Samples per Second。
3. 量化误差(Quantizing Error)由于AD的有限分辩率而引起的误差,即有限分辩率AD的阶梯状转移特性曲线与无限分辩率AD (理想AD)的转移特性曲线(直线)之间的最大偏差。通常是1个或半个最小数字量的模拟变化量,表示为1LSB、 1/2LSB。
4.偏移误差(Offset Error)输入信号为零时输出信号不为零的值,可外接电位器调至最小。
5.满刻度误差(Full Scale Error)满度输出时对应的输入信号与理想输入信号值之差。
6.微分非线性 (Differential nonlinearity, DNL) ADC相邻两刻度之间最大的差异。
7.积分非线性 (Integral nonlinearity, INL)表示了ADC器件在所有的数值点上对应的模拟值和真实值之间误差最大的那一点的误差值,也就是输出数值偏离线性最大的距离。
8.总谐波失真 (Total Harmonic Distotortior缩写 THD)。
02、AD芯片的选取
AD的选择,首先看精度和速度,然后看输入通道数,输出的接口如SPI或者并行的,差分还是单端输入的,输入范围是多少。如何选择你所需要的器件呢?要综合设计的诸项因素,系统技术指标、成本、功耗、安装等,最主要的依据还是速度和精度。
1.精度与所测量的信号范围有关,但估算时要考虑到其他因素,转换器位数应该比总精度要求的最低分辩率高一位。常见的AD/DA器件有8位,10位,12位,14位,16位等。
2.速度根据输入信号的最高频率来确定,保证ADC的转换速率高于系统要求的采样频率。
3.通道有的单芯片内部含有多个AD/DA模块,可同时实现多路信号的转换;常见的多路AD器件只有一个公共的AD模块,由一个多路转换开关实现分时转换。
4. 数字接口方式接口有并行/串行之分,串行又有SPI、 I2C、 SM等多种不同标准。数值编码通常是二进制,也有BCD (二~十进制)、双极性的补码、偏移码等。
5. 模拟信号类型通常AD器件的模拟输入信号都是电压信号,而DA器件输出的模拟信号有电压和电流两种。
6. 同时根据信号是否过零,还分成单极性( Unipolar) 和双极性( Bipolar )。
7. 电源电压有单电源,双电源和不同电压范围之分,早期的AD/DA器件要有+15V/-15V,如果选用单+5V电源的芯片则可以使用单片机系统电源。
8. 基准电压有内、外基准和单、双基准之分。
9.功耗一般CMOS工艺的芯片功耗较低,对于电池供电的手持系统对功耗要求比较高的场合一定要注意功耗指标。
10. 封装形式:常见的封装是DIP,现在表贴型so封装的应用越来越多。
11.跟踪/保持 (Track/Hold 缩写T/H)原则上直流和变化非常缓慢的信号可不用采样保持,其他情况都应加采样保持。
12.满幅度输出(Rail-to Rail)新近业界出现的新概念,最先应用于运算放大器领域,指输出电压的幅度可达输入电压范围。在DA中一般是指输出信号范围可达到电源电压范围。(国内的翻译并不统一,如“轨_轨"、“满摆幅")。
03、针对高精度测量类的AD
参考电压需要足够精确.推荐使用外部高精准参考电压。
如果PGA可调,增益系数一般是越小噪声越低。
一般最好用到满量程,此时AD精度不浪费。
如果有偏置,需要进行自校。
请注意在使用DEMO板调试时,会由调试口导入PC噪声由信号连接线导入外部噪声,因此建议使用屏蔽电缆传输信号。
板上注意模拟电源和数字电源,以及模拟地和数字地要分开;减少耦合噪声路径。
使用差分输入可以减少共模噪声,但是差模噪声会增大。
如果是片内集成AD的MCU,支持高速时钟,如果不影响性能,内部工作时钟越低,对AD采样引起的干扰越小。如果是板上就需要注意走线和分区。
信号输入前级接滤波电路,一般一阶RC电路较多,注意FC=1/1000~1/100采样频率。电阻和电容的参数注意选取,信号接入后级接滤波电路最好采用sinc滤波方式.注意输入偏置电流会限制外部的滤波电阻阻值的大小。R x Ib < 1 LSB。
有的片内AD还有集成输入Buffer,有助于抑制噪声,一般是分两当,看输入信号范围和满量程之间的关系。
AD分为很多种,SARFLASH,并行比较型,逐次逼近型,Delta sigma型,一般是速度越高,精度越高越贵,针对不同场合不同成本不同要求分别选用。
Layout constraint。
04、高速ADC关键指标的定义
一个基本概念
分贝(dB):按照对数定义的一个幅度单位。对于电压值,dB以20log(VA/VB)给出;对于功率值,以10log(PA/PB)给出。dBc 是相对于一个载波信号的dB值; dBm是相对于1mW的dB值。对于dBm而言,规格中的负载电阻必须是已知的(如: 1mW 提供给50Ω),以确定等效的电压或电流值。
静态指标定义
量化误差(Quantization Error):量化误差是基本误差,用图1所示的简单3bit ADC来说明。输入电压被数字化,以8个离散电平来划分,分别由代码000b到111b去代表它们,每一代码跨越Vref/8的电压范围。代码大小一般被定义为一个最低有效位(Least Significant Bit LSB)。若假定Vref=8V时,每个代码之间的电压变换就代表1V。换言之,产生指定代码的实际电压与代表该码的电压两者之间存在误差。一般来说,0.5LSB 偏移加入到输入端便导致在理想过渡点上有正负0.5LSB的量化误差。
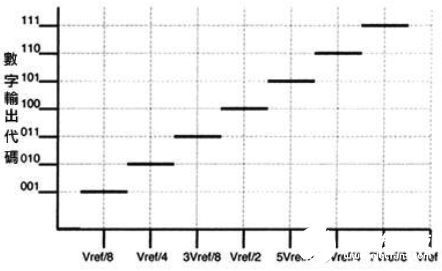
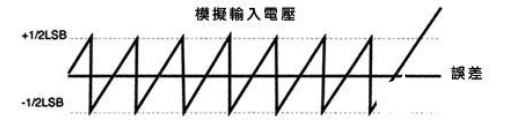
图1 理想ADC转换特性
05、偏移与增益误差(Offset Gain Error)
器件理想输出与实际输出之差定义为偏移误差,所有数字代码都存在这种误差。在实际中,偏移误差会使传递函数或模拟输入电压与对应数值输出代码间存在一个固定的偏移。通常计算偏移误差方法是测量第一个数字代码转换或“零”转换的电压,并将它与理论零点电压相比较。增益误差是预估传递函数和实际斜率的差别,增益误差通常在模数转换器最末或最后一个传输代码转换点计算。
为了找到零点与最后一个转换代码点以计算偏移和增益误差,可以采用多种测量方式,最常用的两种是代码平均法和电压抖动法。代码平均测量就是不断增大器件的输入电压,然后检测转换输出结果。每次增大输入电压都会得到一些转换代码,用这些代码的和算出一个平均值,测量产生这些平均转换代码的输入电压,计算出器件偏移和增益。电压抖动法和代码平均法类似,不同的是它采用了一个动态反馈回路控制器件输入电压,根据转换代码和预期代码的差对输入电压进行增减调整,直到两代码之间的差值为零,当预期转换代码接近输入电压或在转换点附近变化时,测量所施加的“抖动”电压平均值,计算偏移和增益。
06、微分非线性
微分非线性(Differential nonlinearity ,DNL):理论上说,模数器件相邻两个数据之间,模拟量的差值都是一样的。就好比疏密均匀的尺子。但实际上,相邻两刻度之间的间距不可能都是相等的。所以,ADC相邻两刻度之间最大的差异就叫微分非线性DNL,也称为差分非线性。同样举例来说明,如果对于12bit的ADC,其INL=8LSB, DNL=3LSB,在基准电压为4. 095V时,测得A电压对应读数为1000b, 测得B电压对应读数为1200b。那么就可以判断出,B点电压值比A点高出197mV到203mV,而不是准确的200mV。
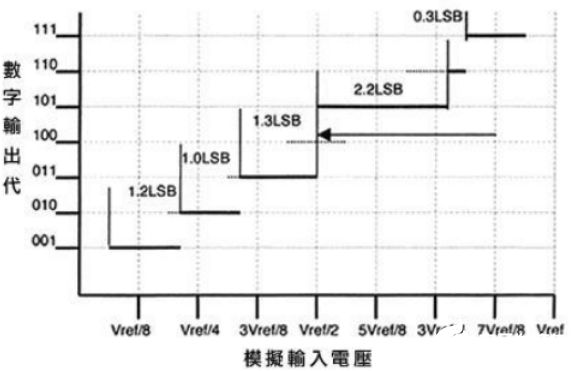
图2 DNL误差特性
图2中,001b 到010b码制过渡过程的DNL为0LSB,因为刚好为1LSB。但是000b到001b过渡就有个0.2LSB的DNL,因为此时有1. 2LSB的代码宽度。应当注意:如果在ADC或者DAC的datasheet中没有清楚说明DNL参数的话,可视该转换器没有漏码,即暗示它有优于正负1LSB的DNL。
07、积分非线性
积分非线性(Integral nonl inearity INL):积分非线性表示了ADC器件在所有的数值点上对应的模拟值和真实值之间误差最大的那一点的误差值,也就是输出数值偏离线性最大的距离。单位是LSB。例如,一个12bit的ADC,INL值为1LSB,那么,对应基准4. 095V,测某电压得到的转换结果是1000b,那么,真实电压值可能分布在0.999V到1.001V之间。
INL是DNL误差的数学积分,即一个具有良好INL的ADC保证有良好的DNL。
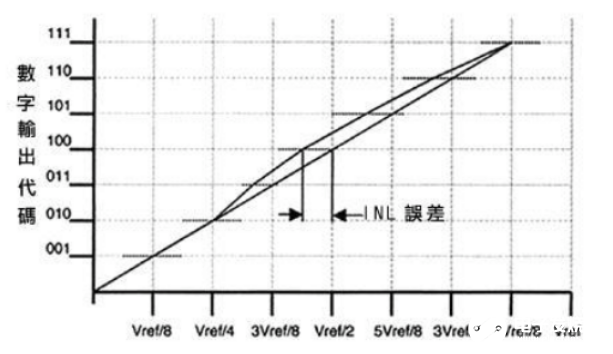
图3 INL误差特性
总之,非线性微分和积分是指代码转换与理想状态之间的差异。非线性微分(DNL)主要是代码步距与理论步距之差,而非线性积分(INL) 则关注所有代码非线性误差的累计效应。对一个ADC来说,一段范围的输入电压产生一个给定输出代码,非线性微分误差为正时输入电压范围比理想的大,非线性微分误差为负时输入电压范围比理想的要小。从整个输出代码来看,每个输入电压代码步距差异累积起来以后和理想值相比会产生一个总差异,这个差异就是非线性积分误差。
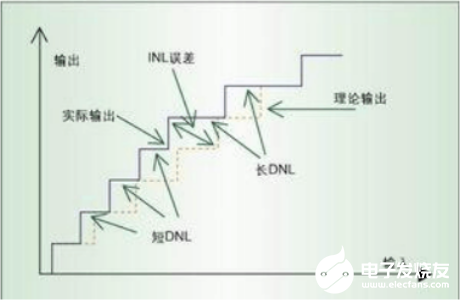
图4 INL和DNL
与增益和偏移一样,计算非线性微分与积分误差也有很多种方法,代码平均和电压抖动两种方法都可以使用,但是由于存在重复搜索,当器件位数较多时这两种方法执行起来很费时。一个更加有效计算INL和DNL的方法是直方图法,采用线性或正弦直方图。图5说明了线性斜升技术的应用,首先使输入电压线性增加,同时对输出以固定间隔连续采样,电压逐步增加时连续几次采样都会得到同样输出代码,这些采样次数称为“点击数”。

图5 计算直方图
从统计上讲,每个代码的点击数量直接与该代码的相应输入电压范围成正比,点击数越多表明该代码的输入电压范围越大,非线性微分误差也就越大;同样,代码点击数越少表明该代码输入电压范围越小,非线性微分误差也就越小。用数学方法计算,如果某个代码点击数为9,而“理想”情况下是8,则该器件的非线性微分误差就是(9-8) /8或0.125。非线性积分是所有代码非线性微分的累计值,对于斜升直方图,它就是每个非线性微分误差的和。从数学观点来看,非线性积分误差等于在代码X-1的非线性微分误差加上代码X和代码X-1的非线性微分误差平均值。
08、动态指标定义
有效位数(ENOB):模数转换器(ADC)与输入频率fIN相关的测试指标(位)。随着fIN 的增大,整体噪声(特别是失真成分)将会增大,因而降低了ENOB和SINAD性能。另请参考:信号与噪声+失真比(SINAD)。
ENOB与SINAD的关系式为:
ENOB =(SINAD-1.76)/6.02
分辨率:模拟信号被量化时,它是以有限的离散电压电平表示的,分辨率是用来表示信号的离散电平个数。为了更精确地恢复模拟信号,必须提高分辨率。分辨率通常定义为位数,利用更高的分辨率进行转换可以降低量化噪声。RMS:参考有关均方根(RMS)的注释。
均坊根(RMS):表示交流信号的有效值或有效直流值。对于正弦波,RMS是峰值的0.707倍,或者是峰~峰值的0.354倍。SFDR:参考有关无杂散动态范围(SFDR)的注释。
信号与噪声+失真比(SINAD):直流到奈奎斯特频段内,正弦波fIN(对于ADC指的是输入正弦波,对于ADC/DAC指的是重建的输出正弦波)的RMS值与转换器噪声的RMS值之比,包括谐波成分。典型值以分贝表示,另请参寺关于均方根(RMS)和总谐波失真的注释。
SINAD = 20log(10) Signal (volts, RMS)/(Noise + Harmonics (volts, RMS))
信噪比(SNR):直流到奈奎斯特频段内,正弦波fIN(对于ADC指的是输入正弦波,对于ADC/DAC指的是重建的输出正弦波)的RMS值之比,直流噪声和谐波失真除外。典型值以分贝表示,另请参考关于均方根(RMS)的注释。
SNR = 20log(10) Signal (volts, RMS)/Noise (volts, RMS)
理想状况下,最小转换噪声的理论值只包括量化噪声,可直接由数据转换分辨率计算得到:
(N):SNR = (6.02N +1.76)dB
无杂散动态范国(SFDR):正弦波fIN(对于ADC指的是输入正弦波,对于ADC/DAC指的是重建的输出正弦波)的RMS值与在频域观察到的杂散信号的RMS值之比,典型值以分贝表示。SFDR在一些需要最大转换器动态范围的通信系统中非常重要。
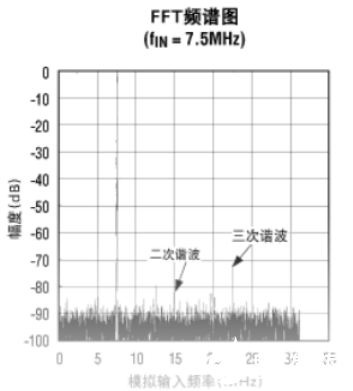
图 6 FFT频谱图
-
adc
+关注
关注
98文章
6500浏览量
544713
发布评论请先 登录
相关推荐
RISC-V芯片中使用的各种常用总线释义
一文带你了解透过率测量
一文带你了解IP地址别名
一文带你了解IP版本

5.8G WiFi和2.4G WiFi如何选择?一文带你深度了解

一文带你了解NVIDIA Jetson

一文带你了解PWM原理、频率与占空比
一文带你了解红墨水实验!




 一文带你了解ADC的参数释义
一文带你了解ADC的参数释义












评论