上一篇我们讲到了最简单的词向量表示方法——共现矩阵(没有看的朋友可以点击这里 小白跟学系列之手把手搭建NLP经典模型(含代码) 回顾一下!)
共现矩阵简单是简单,但是有很严重的问题。
作者强调,自己动手的经验、花时间思考的经验,都是无法复制的。(所以,听话,要自己尝试敲1⃣敲代码噢!
目录
共现矩阵存在的问题:无意义词干扰
余弦相似度:表示两个词向量的相似度
基于计数统计的方法改进
PMI矩阵(排除无意义词干扰)
PPMI矩阵(排除负数)
SVD降维(解决维度爆炸和矩阵稀疏)
总结(用计数统计的方法表示词向量的步骤)
共现矩阵存在的问题
!很多常用的无意义词(比如“the car”)在文中出现次数太多的话,共现矩阵会认为“the”和“car”强相关,这是不合理的!
那怎么表示两个向量之间的相似度呢?
余弦相似度
设有x = (x1,x2,x3,。..,xn)和y = (y1,y2,y3,。..,yn) 两个向量,它们之间的余弦相似度如下式所示。
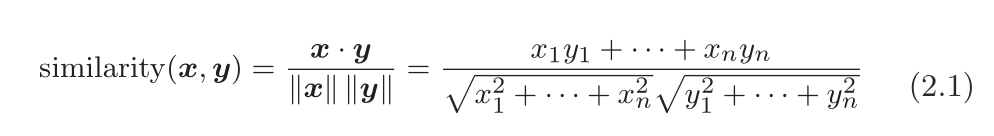
分子为内积,分母为L2范数。(范数表示向量的大小,L2 范数即向量各个元素的平方和的平方根。)
式 (2.1) 的要点是先对向量进行正规化,再求它们的内积。
余弦相似度:两个向量在多大程度上指向同一方向。也就是说,余弦相似度越靠近1,两个词越相似;余弦相似度越靠近0,两个词越没什么关系;
现在,我们来代码实现余弦相似度。
def cos_similarity(x, y): # x 和 y 是 NumPy 数组 nx = x / np.sqrt(np.sum(x**2)) # x的正规化 ny = y / np.sqrt(np.sum(y**2)) # y的正规化 return np.dot(nx, ny)
为了防止除数为0(比如0向量),所以要给分母加个微小值eps=10^-8
修改后的余弦相似度的实现如下所示(common/util.py)。
def cos_similarity(x, y, eps=1e-8): nx = x / (np.sqrt(np.sum(x ** 2)) + eps) ny = y / (np.sqrt(np.sum(y ** 2)) + eps) return np.dot(nx, ny)
在绝大多数情况下,加上eps不会对最终的计算结果造成影响,因为根据浮点数的舍入误差,这个微小值会被向量的范数“吸收”掉。而当向量的范数为 0 时,这个微小值可以防止“除数为 0”的错误。
利用这个cos_similarity函数,可以求得单词向量间的相似度。我们尝试求you 和I的相似度(ch02/similarity.py)。
import syssys.path.append(‘。.’)from common.util import preprocess, create_co_matrix, cos_similarity# 引入文本预处理,创建共现矩阵和计算余弦相似度的函数 text = ‘You say goodbye and I say hello.’corpus, word_to_id, id_to_word = preprocess(text) # 文本预处理vocab_size = len(word_to_id)C = create_co_matrix(corpus, vocab_size) # 创建共现矩阵 c0 = C[word_to_id[‘you’]] # you的词向量c1 = C[word_to_id[‘i’]] # i的词向量print(cos_similarity(c0, c1)) # 计算余弦相似度# 0.7071067691154799
从上面的结果可知,you 和 i 的余弦相似度是 0.70 。 . 。,接近1,即存在相似性。
说完单词向量之间的相似度可以余弦相似度表示,用共现矩阵的元素表示两个单词同时出现的次数。而很多常用的无意义词(比如“the car”)在文中出现次数太多的话,共现矩阵会认为“the”和“car”强相关,这是不合理的!
所以共现矩阵中无意义词的干扰怎么解决呢?
基于计数的方法改进
接下来将对共现矩阵进行改进,并使用更实用的语料库,获得单词“真实的”分布式表示。
点互信息
引入点互信息(Pointwise Mutual Information,PMI)这一指标。即考虑单词单独出现的次数。无意义词(“the”)单独出现次数肯定多,这点要考虑进去。
对于随机变量 x 和 y,它们的 PMI 定义如下:
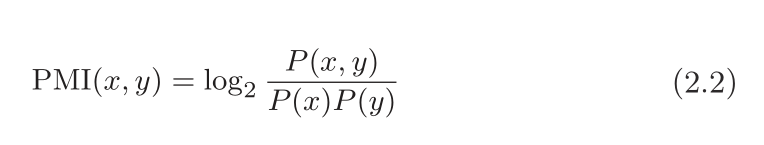
P(x) 表示 x 发生的概率,
P(y) 表示 y 发生的概率,
P(x, y) 表示 x 和 y 同时发生的概率。
PMI 的值越高,表明相关性越强。
例如设X = “the”,Y = “car”
P(“the”) = “the”出现的次数
P(“car”) = “car”出现的次数
P(“the car”) = “the car”共同出现的次数
“the”单独出现的次数多,所以P(“the”)分母也就大,也就抵消掉了the的作用啦。
怎么表示概率呢?简单的方式就是用共现矩阵来表示概率,因此也能表示出PMI。也就是用单词出现的次数表示概率。
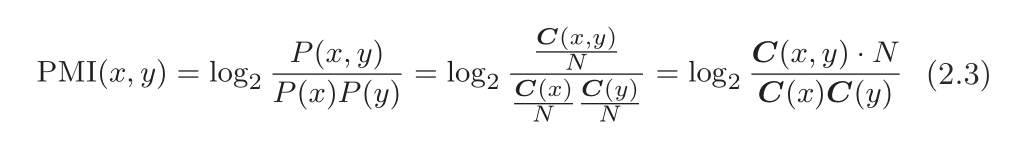
N:语料单词总数;
C(X):X出现的次数 ;
C(X,Y):X,Y共现的次数;
举个栗子:
这里假设有一个文本语料库。单词总数量(N)为 10 000,the 出现 100 次,car 出现 20 次,drive 出现 10 次,the 和 car 共现 10 次,car 和 drive 共现 5 次。 这时,如果从共现次数的角度来看,the 和 car 的相关性更强。 而如果从 PMI 的角度来看,结果是怎样的呢?
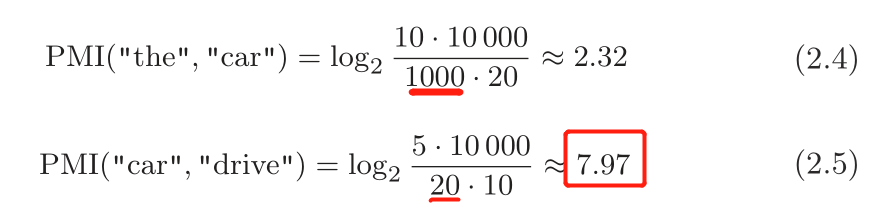
结果表明,在使用 PMI 的情况下,drive 和 car 具有更强的相关性。这是我们想要的结果。之所以出现这个结果,是因为我们考虑了单词单独出现的次数。因为 the 本身出现得多,所以 PMI的得分被拉低了。
但也存在一个问题。
当两个单词的共现次数为 0 时,log20 = −∞。为了解决这个问题,实际上我们会使用正的点互信息(Positive PMI,PPMI)。
解决办法
用PPMI (Positive PMI,正的点互信息)来表示词之间的相关性
正的点互信息
PPMI(x,y) = max(0, PMI(x,y)) ,即当PMI为负数的时候,视作0。
所以,PPMI构建的矩阵要优于共现矩阵(因为排除了像the等无意义词的干扰呀)。所以PPMI是更好的词向量。
实现将共现矩阵转化为PPMI 矩阵的函数为 ppmi(C, verbose=False, eps=1e-8)。这里不再赘述,我们只需要调用,需要看源代码的去(common/util.py)
如何调用使用它呢?可以像下面这样进行实现(ch02/ppmi.py)。
import syssys.path.append(‘。.’)import numpy as npfrom common.util import preprocess, create_co_matrix, cos_similarity,ppmi text = ‘You say goodbye and I say hello.’corpus, word_to_id, id_to_word = preprocess(text) # 文本预处理vocab_size = len(word_to_id)C = create_co_matrix(corpus, vocab_size) # 创建共现矩阵W = ppmi(C) # 将共现矩阵 ——》 PPMI 矩阵np.set_printoptions(precision=3) # 设置有效位数为3位print(‘covariance matrix’)print(C)print(‘-’*50)print(‘PPMI’)print(W)
运行该文件,可以得到:
covariance matrix[[0 1 0 0 0 0 0] [1 0 1 0 1 1 0] [0 1 0 1 0 0 0] [0 0 1 0 1 0 0] [0 1 0 1 0 0 0] [0 1 0 0 0 0 1] [0 0 0 0 0 1 0]]--------------------------------------------------PPMI[[ 0. 1.807 0. 0. 0. 0. 0. ] [ 1.807 0. 0.807 0. 0.807 0.807 0. ] [ 0. 0.807 0. 1.807 0. 0. 0. ] [ 0. 0. 1.807 0. 1.807 0. 0. ] [ 0. 0.807 0. 1.807 0. 0. 0. ] [ 0. 0.807 0. 0. 0. 0. 2.807] [ 0. 0. 0. 0. 0. 2.807 0. ]]
这样一来,我们就成功的将共现矩阵转化为了 PPMI 矩阵啦,也获取了一个更好的单词向量!
但是PPMI矩阵也存在很明显的问题
维度爆炸
矩阵稀疏
如果语料库的词汇量达到10 万,则词向量的维数也同样达到 10 万。处理 10 万维向量是不现实的。
另外,我们可以看得出该矩阵很多元素都是 0。这表明向量中的绝大多数元素并不重要,也就是说,每个元素拥有的“重要性”很低。这样的向量也容易受到噪声影响,稳健性差。
对于这些问题,一个常见的方法是向量降维。
解决办法:降维
降维:减少向量维度(尽量保留重要信息)。发现重要的轴/分布广的轴,将二维数据变一维数据。
目的:从稀疏矩阵中找到重要的轴,用更少的维度去表示词向量。
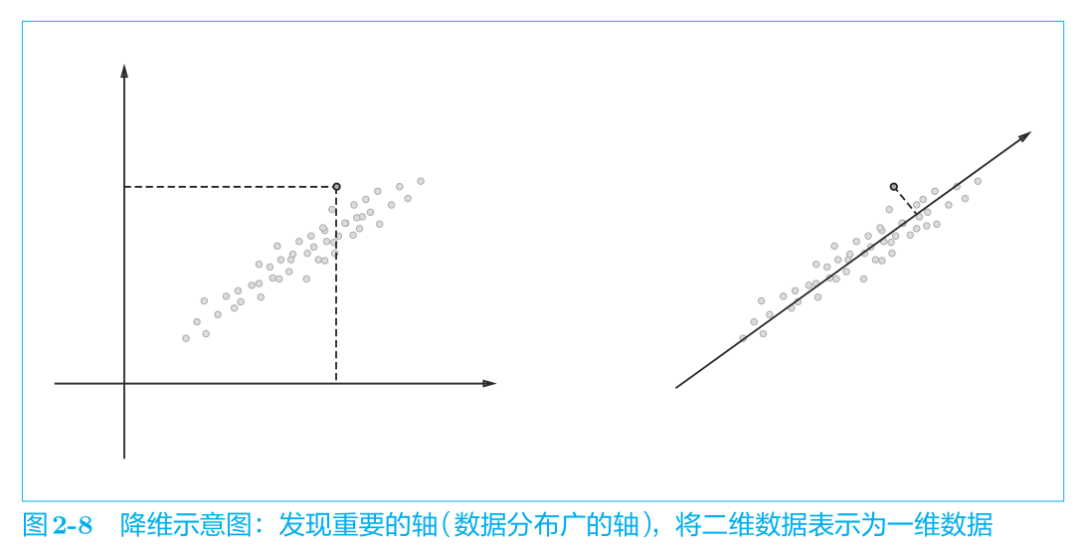
降维的方法有很多,这里我们使用奇异值分解(Singular Value Decomposition,SVD),如下式所示:

SVD 将任意的矩阵 X 分解为 U、S、V 这 3 个矩阵的乘积,其中 U 和 V 是列向量彼此正交的正交矩阵,S 是除了对角线元素以外其余元素均为 0 的对角矩阵。
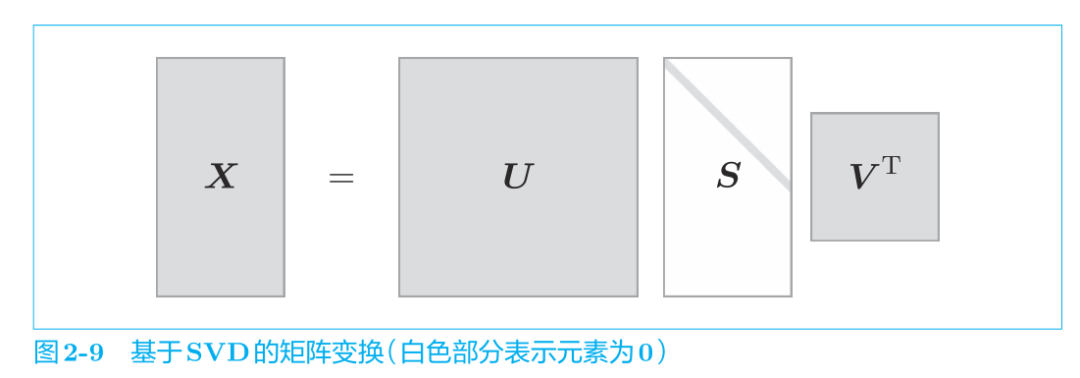
在式 (2.7) 中,U 是正交矩阵。这个正交矩阵构成了一些空间中的基轴(基向量),我们可以将矩阵 U 作为“单词空间”。
S 是对角矩阵,奇异值在对角线上降序排列。
简单地说,我们可以将奇异值视为“对应的基轴”的重要性。这样一来,如图 2-10 所示,减少非重要元素就成为可能。
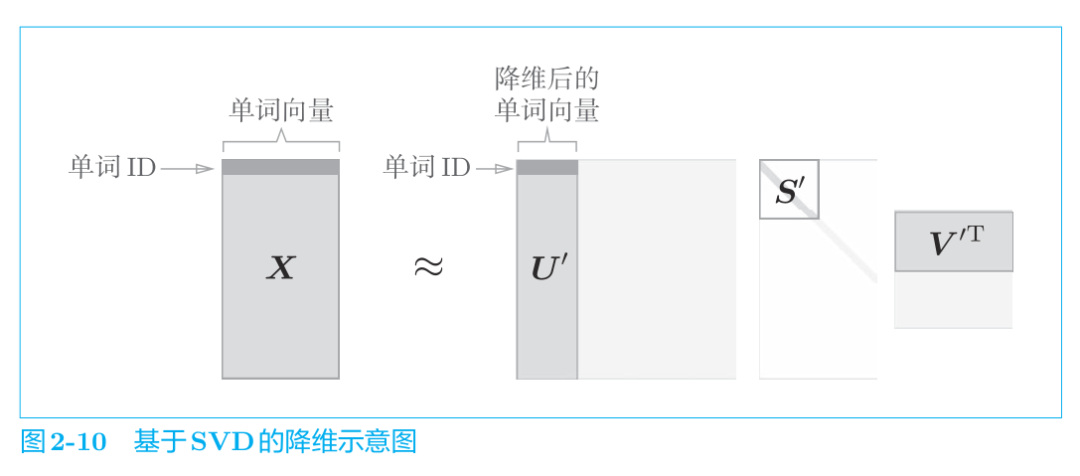
如图 2-10 所示,矩阵 S 的奇异值小,对应的基轴的重要性低,因此,可以通过去除矩阵 U 中的多余的列向量来近似原始矩阵。用我们正在处理的“单词的 PPMI 矩阵”来说明的话,矩阵 X 的各行包含对应的单词 ID的单词向量,这些单词向量使用降维后的矩阵 U‘表示。
想从数学角度仔细理解SVD的读者,请参考文献[20] 等。
接下来将用代码实现 SVD ,这里可以使用 NumPy 的linalg模块中的 svd 方法。linalg 是 linear algebra(线性代数)的简称。下面,我们创建一个共现矩阵,将其转化为 PPMI 矩阵,然后对其进行 SVD降维(h02/count_method_small.py)。
import syssys.path.append(’。.‘)import numpy as npimport matplotlib.pyplot as pltfrom common.util import preprocess, create_co_matrix, ppmi text = ’You say goodbye and I say hello.‘corpus, word_to_id, id_to_word = preprocess(text)vocab_size = len(id_to_word)C = create_co_matrix(corpus, vocab_size, window_size=1)W = ppmi(C) # SVDU, S, V = np.linalg.svd(W) # 变量U已成为密集向量
SVD 执行完毕。上面的变量 U 包含经过 SVD 转化的密集向量表示(稀疏的反义词,就是没那么多0啦)。现在,我们来看一下它的内容。单词 ID 为 0 的单词向量you如下。
print(C[0]) # 共现矩阵(简单的用次数来表示)# [0 1 0 0 0 0 0] print(W[0]) # PPMI矩阵(用PPMI指标(概率)表示)# [ 0. 1.807 0. 0. 0. 0. 0. ] print(U[0]) # 做了SVD降维# [ 3.409e-01 -1.110e-16 -1.205e-01 -4.441e-16 0.000e+00 -9.323e-01# 2.226e-16]
如上所示,原先的稀疏向量 W[0] 经过 SVD 被转化成了密集向量 U[0]。
但SVD同样也有缺点:速度太慢
加快方法:采用Truncated SVD(截去奇异值较小的部分,实现高速化)
如果矩阵大小是 N,SVD 的计算的复杂度将达到 O(N3)。这意味着 SVD 需要与 N 的立方成比例的计算量。现实中这样的计算量是做不到的,所以往往会使用 Truncated SVD等更快的方法。
Truncated SVD 通过截去(truncated)奇异值较小的部分,从而实现高速化。下面,我们将使用 sklearn库的 Truncated SVD。
以上都是用的一句话语料来举的例子,接下来要来“真的”了!
使用真的更大的语料库:Penn Treebank(PTB数据集)
PTB数据集
这个 PTB 语料库是以文本文件的形式提供的,与原始的 PTB 的文章相比,多了若干预处理,包括将稀有单词替换成特殊字符 《unk》( unknown 的简称),将具体的数字替换成“N”等。
作为参考,图 2-12 给出了 PTB 语料库的部分内容。一行保存一个句子。

这里,我们还要将所有句子连接起来,在每个句子的结尾处插入一个特殊字符 《eos》(end of sentence 的简称)。
接下来我们将代码实现如何使用PTB数据集。
import syssys.path.append(’。.‘)from dataset import ptb corpus, word_to_id, id_to_word = ptb.load_data(’train‘) # 训练用数据 print(’corpus size:‘, len(corpus))print(’corpus[:30]:‘, corpus[:30])print()print(’id_to_word[0]:‘, id_to_word[0])print(’id_to_word[1]:‘, id_to_word[1])print(’id_to_word[2]:‘, id_to_word[2])print()print(“word_to_id[’car‘]:”, word_to_id[’car‘])print(“word_to_id[’happy‘]:”, word_to_id[’happy‘])print(“word_to_id[’lexus‘]:”, word_to_id[’lexus‘])
结果如下所示:
corpus size: 929589 # 数据集中词总数corpus[:30]: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 20 21 22 23 24 25 26 27 28 29] id_to_word[0]: aerid_to_word[1]: banknoteid_to_word[2]: berlitz word_to_id[’car‘]: 3856word_to_id[’happy‘]: 4428word_to_id[’lexus‘]: 7426
和之前一样,corpus 中保存了单词 ID 列表,id_to_word 是将单词 ID 转化为单词的字典,word_to_id 是将单词转化为单词 ID 的字典。
如上面的代码所示,使用 ptb.load_data() 加载数据。此时,指定参数 ’train‘、’test‘ 和 ’valid‘ 中的一个,它们分别对应训练用数据、测试用数据和验证用数据中的一个。以上就是 ptb.py 文件的使用方法。
加载PTB数据集的代码 :dataset/ptb.py
使用PTB数据集的例子:ch2/show_ptb.py
基于计数(统计)的方法利用PTB数据集的代码:ch02/count_method_big.py
总结
词向量表示总共介绍了:
基于同义词词典的方法
基于计数统计的方法
同义词词典需要人工定义词之间的相关性,很费力;
使用计数统计的方法可以自动的获取词向量表示。
用计数统计的方法表示词向量的步骤:
使用语料库(使用语料库对单词进行向量化是主流方法)
计算上下文单词共同出现的次数(共现矩阵)
转化为PPMI矩阵(为了减少无意义词的干扰)
基于SVD降维(解决维度爆炸和矩阵稀疏问题,以提高稳健性)
从而获得了每个单词的分布式表示,也就是词向量表示,每个单词表示为固定长度的密集向量。(单词的分布式表示=词向量表示)
在单词的向量空间中,含义上接近的单词距离上也更接近。
使用语料库对单词进行向量化是主流方法。
其实在海量数据的今天,基于计数统计的方法难以处理大规模的数据集,统计方法是需要一次性统计整个语料库,需要一次性处理全部的数据,而SVD降维的复杂度又太大,于是将推出——基于推理的方法,也就是基于神经网络的方法。
神经网络一次只需要处理一个mini-batch的数据进行学习,并且反复更新网络权重。
基于推理(神经网络)的方法,最著名的就是Word2Vec。下一次我们会详细的介绍它的优点缺点以及使用方法噢!
原文标题:小白跟学系列之手把手搭建NLP经典模型-2(含代码)
文章出处:【微信公众号:深度学习自然语言处理】欢迎添加关注!文章转载请注明出处。
责任编辑:haq
-
神经网络
+关注
关注
42文章
4772浏览量
100855 -
nlp
+关注
关注
1文章
489浏览量
22052
原文标题:小白跟学系列之手把手搭建NLP经典模型-2(含代码)
文章出处:【微信号:zenRRan,微信公众号:深度学习自然语言处理】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
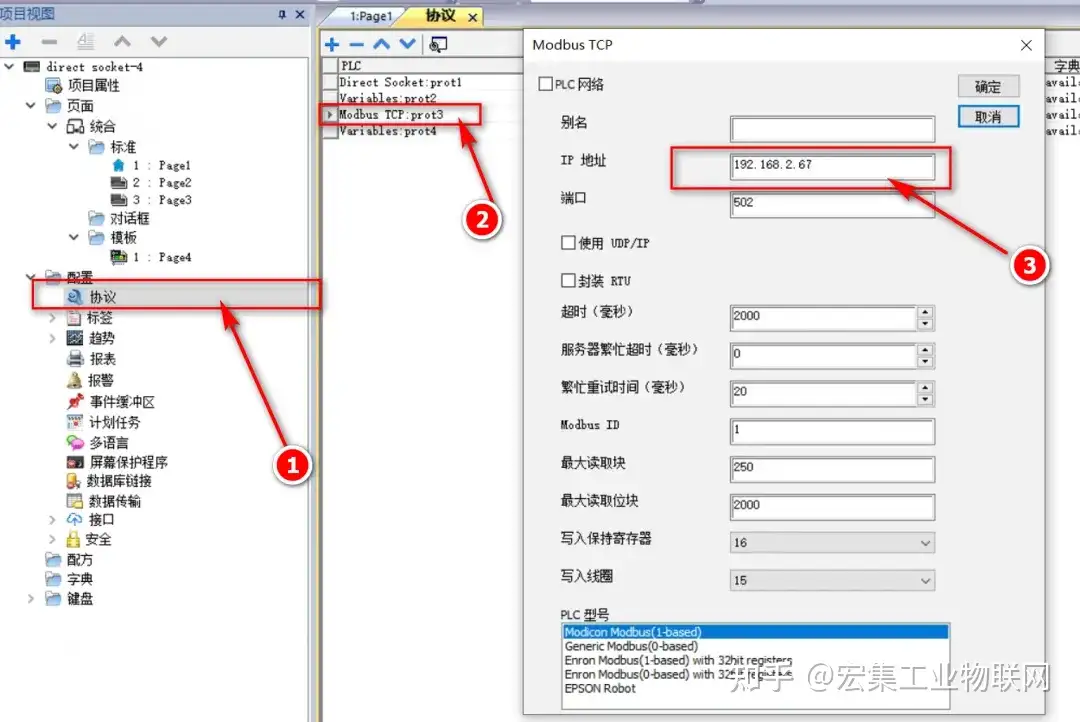
手把手教你通过宏集物联网工控屏&网关进行协议转换,将底层PLC/传感器的数据转换为TCP协议并传输到用户
nlp逻辑层次模型的特点
nlp自然语言处理模型怎么做
使用PyTorch搭建Transformer模型
手把手教你使用物模型连接DDSU电表

手把手教你排序算法怎么写

无刷电机无感FOC控制培训系列课程
【飞腾派4G版免费试用】4.手把手玩转QT界面设计
使用DPort-ECT搭建EtherCAT从站step by step





 手把手教你搭建NLP经典模型
手把手教你搭建NLP经典模型












评论