开关电源反馈补偿网络的应用设计

开关电源的输出是直流输入电压、占空比和负载的函数。在开关电源设计中，反馈系统的设计目标是无论输入电压、占空比和负载如何变化，输出电压总在特定的范围内，并具有良好的动态响应性能。

电流模式的开关电源有连续电流模式（CCM）和不连续电流模式（DCM）两种工作模式。连续电流模式由于有右半平面零点的作用，反馈环在负载电流增加时输出电压有下降趋势，经若干周期后最终校正输出电压，可能造成系统不稳定。因此在设计反馈环时要特别注意避开右半平面零点频率。

当反激式开关电源工作在连续电流模式时，在最低输入电压和最重负载的工况下右半平面零点的频率最低，并且当输入电压升高时，传递函数的增益变化不明显。当由于输入电压增加或负载减小，开关电源从连续模式进入到不连续模式时，右半平面零点消失从而使得系统稳定。因此，在低输入电压和重输出负载的情况下，设计反馈环路补偿使得整个系统的传递函数留有足够的相位裕量和增益裕量，则开关电源无论在何种模式下都能稳定工作。

1 反激式开关电源典型设计

图1是为变频器设计的反激式开关电源的典型电路，主要包括交流输入整流电路，反激式开关电源功率级电路（有PWM控制器、MOS管、变压器及整流二极管组成），RCD缓冲电路和反馈网络。其中PWM控制芯片采用UC2844。UC2844是电流模式控制器，芯片内部具有可微调的振荡器（能进行精确的占空比控制）、温度补偿的参考基准、高增益误差放大器、电流取样比较器。

开关电源设计输入参数如下：三相380V工业交流电经过整流作为开关电源的输入电压Udc，按最低直流输入电压Udcmin为250V进行设计；开关电源工作频率f为60kHz，输出功率Po为60W。

当系统工作在最低输入电压、负载最重、最大占空比的工作情况下，设计开关电源工作在连续电流模式（CCM），纹波系数为0．4。设计的开关电源参数如下：

变压器的原边电感Lp=4．2mH，原边匝数Np=138；5V为反馈输出端，U5V=5V，负载R5=5Ω，匝数N5V=4，滤波电容为2个2200μF／16V电容并联，电容的等效串联电阻Resr=34mΩ；24V输出的负载R24=24Ω，匝数N24V=17；15V输出的负载R15=15Ω，匝数N15V=1l；一1 5V输出的负载R-15V=15Ω，匝数N-15V=11。

2 功率级电路的传递函数

电流模式控制器控制框图包含两个反馈环，外部电压环反馈电压信息，内部电流环反馈电流信息（如图2所示）。电流环的输入是控制电压UC和电感电流采样值US的差值，电流环的输出是占空比D。当US小于UC时，PWM调制器（Fm）输出高电平，功率开关开通，当US大于UC，PWM调制器输出低电平，功率开关关断。通过具有固定频率时钟信号的RS触发器，下一个周期自动置位。通过这种方式，电感峰值电流被控制电压精确控制。

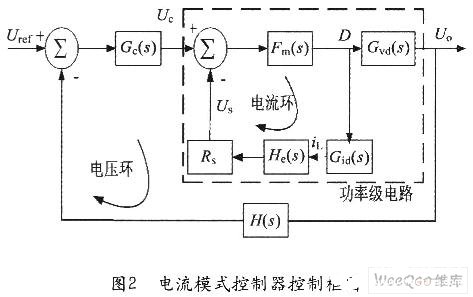
控制框图中Gvd（s）是功率级电路占空比控制端到输出电压的传递函数，Gid（S）为占空比控制端到电感电流的传递函数，Fm（s）为PWM调制器的增益函数，He（s）为电流模式控制的开环采样增益，Rs为电流采样电阻，Uref为基准参考电压。

基于文献建立的反激式开关电源的交流小信号数学模型和Vorperian建立的简化平均PWM开关模型以及Ridley Engirleering建立的电流模式的数学模型，建立反激式开关电源的等效电路模型，进而可以求得各环节的传递函数。

从控制到输出的传递函数如下：

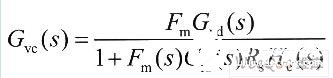
Gvd（s）和Gid（s）都具有双极点，但当电流环增益足够大，它们的双极点可以抵消，从而可以得到如下近似的具有单极点的传递函数：

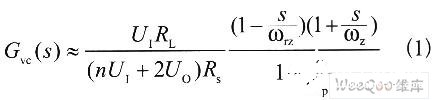
其中：UI为直流输入电压，Uo为输出电压，RL为等效负载电阻，RS为电流采样电阻，n=Ns/Np为变压器的匝数比。

零极点计算如下：

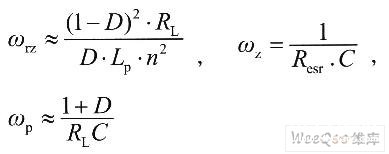
其中D为占空比，Lp为初级电感，RL为负载电阻，C为输出电容，Resr为输出电容等效串联电阻。

由（1）式可以求得图1所示开关电源从控制到输出的传递函数：

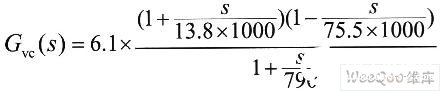
其中对于多路输出的负载RL，是指控制输出端的等效负载。按照文献提供的思路，将其他各路输出都“映射”到5V反馈输出，从而可以得到：

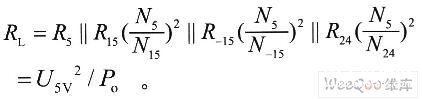
右半平面零点频率frz=ωrz／2π=12kHz，电容等效串联电阻ESR零点频率fz=ωz／2π=2．2kHz，负载极点频率fp=ωp／2π=125kHz。

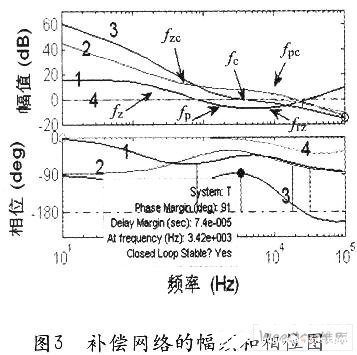
控制到输出的传递函数伯德图如图3所示，曲线1分别为其幅频和相位图。该图利用Matlab提供的伯德图分析工具绘制。

3 反馈补偿网络设计

反馈环节由电压采样网络He（s），误差放大器Gc（s）和辅助补偿环节Gx（s）组成，则系统的开环传递函数T（s）=H（s）Gc（s）Gx（s）Gvc（s）。其中电压采样网络H（s）=R1／（R1+R2），误差放大器有TL43l和光耦TLP781构成，辅助补偿环节包括电阻Rx和电容Cr。

由反馈网络补偿后得到的开环传递函数T（s）判断反馈系统的工作性能，要满足如下三个准则：

1）足够大的开环传递函数增益|T|使得输出U（s）接近于Uref（s）／H（s），并且与前向传递函数的增益关系不大，具有很好的抗干扰能力。

2）为防止一40dB／10倍频程增益斜率的电路相位快速变化，系统的闭环增益曲线在穿越频率附近的增益斜率应为一20dB／10倍频程。

3）在穿越频率处保证足够大的开环传递函数的相位裕度，一般至少45°；在T（s）的相位为一180°时，保证幅值裕度Gm≤一10dB。

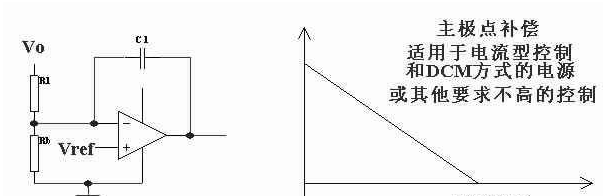
基于以上的准则设计了由TL43l和光耦TLP781组成的双极点单零点反馈补偿网络，TL431内部的电压基准Uref≈2．5 V。设计中略过了U C2844的内部误差放大器，直接把反馈输入信号接在误差放大器的输出端l脚，利用TL431构成反馈补偿环节。这种设计可以把反馈信号的传输时间缩短一个放大器的传输时间，使电源的动态响应更快。

误差放大器从误差输入信号到控制端的传递函数：

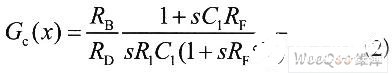
其中RB为UC2844内部0．5mA电流源的等效电阻，RB≈5kΩ，RD=200Ω。

补偿零点fzc=l／（2πC1RF），补偿极点fpc=1／（2πC2RF）。

反馈补偿网络设计的步骤如下：

1）将穿越频率设定为右半平面零点频率的l／4处，即fc=1／4frz=3kHz。

2）设定补偿零点fzc=1／3fc=l kHz，补偿极点fpc=3fc=9kHz，满足fc/fzc=fpc/fc。

3）通过计算可得C1=lOnF，C2=100nF，RF=1．5kΩ。由于反馈补偿网络影响开环传递函数的特性，通过上式得到的补偿网络可能并不满足设定的穿越频率，因此可以借助Matlab提供的伯德图分析工具配置参数，直到达到所需要的控制性能，图3中的曲线2为较理想的补偿曲线。

补偿零点的设计要考虑低频三相整流谐波（1 50Hz），补偿极点的设计考虑右半平面零点频率，并且要综合考虑相位裕量和稳定带宽的关系，最终调节的参数如下：

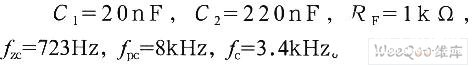
另外，当负载RL较小，初级电感Lp较大时，右半平面零点频率可能较低，这样就会造成反馈稳定的频带较窄，同时可能达不到所要求的幅值裕度Gm≤一10dB。为此，引入由Rx、Cx构成的辅助补偿网络，与内部等效电阻RB构成辅助零极点补偿，进一步抵消右半平面零点频率的影响，使得反馈回路在满足幅值裕度和相位裕度的前提下，能获得较大的环路增益。

辅助补偿的零点fzx=l／（2πCxRx），辅助补偿的极点fpx=1／（2πCxRB）。其中，fpx一般设计在frz附近，fzx=3fpx。辅助补偿网络的幅频和相位曲线如图3中曲线4所示。

反馈网络补偿后总开环传递函数T（s）的幅频和相频特性曲线如图3中曲线3所示。由于三相整流电路产生的直流输入具有三相交流输入的3次谐波（150Hz），因此需要开关电源在低频处有很好的频率响应特性，通过调节RD的值得到较大的增益|T|；通过设计反馈补偿网络，使得开环传递函数T（s）在穿越频率fc处的斜率为一20dB／10倍频程，并且具有91°的相位裕度（如图3所示）。因此，设计的反馈补偿网络是成功的，开关电源能够稳定工作并且具有很好的动态响应特性。

4 实验分析

为测试所设计的开关电源的稳定性和动态响应性能，设计如下的实验：将负载由半载到满载突变和满载到半载突变（包括5V反馈负载突变），观察5V的输出波形，实验波形如图4所示。

图4中上方所示为当负载突变时5V输出波形图（每格50mV），下方为上方波形的区间放大。5V输出电压为4．99V（电压值通过配置电压采样网络R1和R2得到），满载时纹波40mV，半载时纹波14mV。当负载由半载到满载突变（5V由空载到满载），5V电压下降大约20mV时反馈系统开始响应，并迅速调整输出电压值，在O．5ms的时间内达到新的平衡；当负载由满载到半载突变时，5V电压也仅有大约20mV的波动。由此可见，反馈系统具有良好的稳定性和动态响应特性。

5 结束语

反馈环节的设计是开关电源设计的关键也是设计的难点。本文在分析电流模式反激式开关电源控制框图的基础上得到了各个环节的传递函数，从而为反馈补偿网络的设计奠定了理论基础，再结合Matlab提供的伯德图分析工具，得到了优化的反馈补偿网络电路参数，很好的解决了棘手的反激式开关电源反馈稳定性和动态响应性问题。

责任编辑：gt