数字信号处理的相位为什么很重要？

学习数字信号处理的诀窍：复数或向量的运用

学好数字信号处理的诀窍之二——复数与向量的运用

信号的相位为什么很重要

一、学好数字信号处理的诀窍之二——复数和向量的运用 在学习复数之前，我们学过的实数可以称为一元数，它只有一个维度，即大小。复数是二元数，它有两个维度，即实数部分和虚数部分，也可以说幅度和相位角。由于复数的维度比实数多一个，因而得到很多精彩的应用。(顺便介绍一下，三元数是不存在的，但是英国数学家哈密尔顿发明了四元数，后来的一些数学家陆续发明了八元数、十六元数，但随着元数的增加，其应用价值微乎其微。) 向量是一种既有大小又有方向的量，是和标量相对的，向量在现实中是广泛存在的，复数处理这种既有大小又有方向的量即向量时，表现出极大的简洁性。复数和向量在信号分析和处理中可以使复杂问题简单化、直观化，是理解数字信号处理非常有力的工具。此外，复数在表示既有一定大小、又有一定相位的量如正弦信号时，表现出很大的优越性。

复数的用途表现在它同时包含了向量的幅度和相位信息，因而给计算和公式的表达带来很大的方便。复数是工程中最强大的工具之一，可以这么说，没有复数这种工具，近代工业文明简直是不可想象的。下面举几个例子说明复数的应用。 1、傅里叶变换。没有复数作为工具，周期信号分解的表达式将会比较复杂，而用复数表达则异常简洁、美观，便于数学分析。 高等数学讲过傅里叶级数的内容，连续周期信号f(t)可以展开为无穷级数，设f(t)的周期为T，则角频率为Ω = 2π/T，可以分解为：

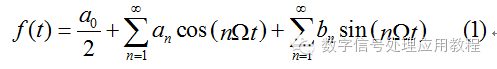
式中的系数an(n = 0, 1, 2,…), bn(n = 1, 2, …)分别为：

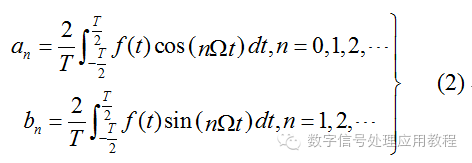
上面的表达式物理意义很明确，但是计算很繁琐，并且在实际中无需区分频率相同的正弦和余弦信号，因为同频的正弦和余弦信号之和还是同频的信号，只是幅度和相位发生了改变(下面将谈到信号的相位的重要性)。《信号与系统》里面引进复指数形式的信号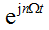后，上面的公式(1)和(2)简化为：    

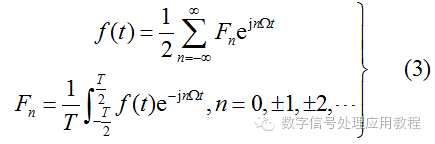
直观上看，公式(3)比公式(1)和(2)之和要简洁很多，它们包含的信息量是完全一样的，但是式(3)更方便进行数学分析。 2、系统函数。利用复数可以很方便地表示信号经过一个系统(模拟的或数字的)之后各个频率成分的变化情况，因为系统不仅改变输入信号各个频率分量的幅值大小，也改变相对相位的大小，而信号的相位是很重要的物理量，该系统称为滤波器，可以实现各种功能。没有复数作为工具，对系统的变换特性进行描述是极其困难的。 下面是一个有趣的问题：某人向东走1公里后，向左拐走1/2公里，再向左拐走(1/2)2公里，……，如此不停地进行下去，问这个人最后停留在什么位置？ 用复数解决很简单，初始位置到最后停留位置连线的复数为

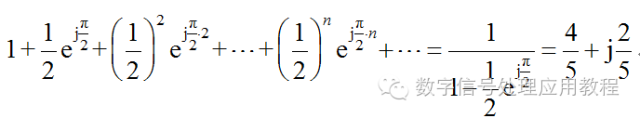
即某人最终位于起始位置的偏东4/5公里、偏北2/5公里的位置。很多同时涉及距离和角度的题目用复数解决都很简单，复数在中学竞赛中也得到重要应用。 二、为什么信号的相位很重要 任何信号(周期或非周期，连续或离散)都可以分解为不同频率的余弦信号加权和。余弦信号由三个参数确定：幅度、相位和频率，这三个参数的地位是同等重要的，相位的重要性可以通过以下几个具体例子看出来。

1、两个同频率的余弦信号相互叠加，当相位相同时将互相加强，一个实际的例子是，当部队过大桥时，为了避免走正步的频率和大桥的固有频率同相而加强，导致共振破坏大桥，因此部队过大桥时都走碎步；当两个同频余弦信号相位正好相反时，将互相减弱，甚至可以抵消为零。两个同频信号的叠加，相对相位的不同将导致结果差异很大。 2、国庆典礼上军人的步伐高度一致，给人一种难以言说的美感和震撼感，从数学上来说就是“相位”高度一致。 3、有一句谚语“海上无风三尺浪”，这是因为海上不同的船只都独立产生一个类似余弦波，很多的波合成时，在某些相对相位情况下互相叠加而加强。

4、一个信号的不同频率成分，经过一个系统之后，如果相对“相位”发生了改变，即有的频率成分“超前”了，有的频率成分“落后”了，那么合成之后的信号就会发生失真，而很多情况是要求信号不失真地传输的，如图像信号等。当然，有时对信号进行有目的“失真”处理也是必要的，比如将含有噪声的信号进行去噪。 总之，掌握好复数和向量，是学好数字信号处理等课程的一个诀窍，这是由复数可以同时表示幅度和相位的性质决定的。

原文标题：学好数字信号处理的诀窍之二——复数和向量的运用

文章出处：【微信公众号：数字信号处理辅导】欢迎添加关注！文章转载请注明出处。

责任编辑：haq