设计要求
利用matlab设计一个线性相位FIR带通滤波器,并在FPGA上实现。
1、滤波器指标:过渡带带宽分别为100~300HZ,500~700HZ,阻带允许误差为0.02,通带允许误差为0.01,采样频率为2000HZ,量化位数为12bit
2、设计方法,要求利用kaiserord函数获取滤波器参数,并设计成等波纹最优滤波器
3、要求对叠加信号进行滤波,叠加信号是由频率分别为100 ,400,800HZ的正弦波叠加而成,要求将信号通过FPGA滤波后的用modelsim仿真,并在matlab中验证滤波器的正确性
很多朋友一看,这是嘛呀?即使当时数字信号处理学的还算可以,但是真正到工程中就傻了眼了,好吧,半个月前我也是这种状态,下面我就记录一下这段时间学这部分知识的过程吧
1、嘛叫滤波器?
我们所说的当然就是数字滤波器了,官方解释就是输入输出都是数字信号,通过数值运算处理改变输入信号所含频率成分相对比例,或者滤除某些频率成分的数字器件或者程序。对于经典滤波器而言,就是利用了当信号有用成分的频带与想要滤除的信号的频带是不叠加的,占据不同频率带的这一特点,利用经典滤波器,包括低通,高通,带通,带阻滤波器,设计制定的通带,滤除不需要的信号成分,得到我们想要频带信号的过程。但是对于信号的频带相互叠加的情况,经典滤波器就无能为力了,就需要用到现代滤波器,当然也就更高大上了,我水平有限,也不知道他是嘛了~
而我们常用的滤波器就是选频滤波器了,就像上面那个我给大家出的题目就是一个选频滤波器。学过数字信号处理的同学应该知道,我们要观察信号的频域,需要将其进行傅里叶变换,得到信号的频率响应,这个响应我们用H(e^jw)表示,频率响应又可以分为幅频响应与相频响应,幅频响应表示的是信号经过滤波器滤波后频率成分幅度的衰减情况,相频响应表示的是信号经滤波器滤波后的延时情况,因此我们往往通过这两个特性来观察我们的滤波器是否符合我们的设计要求。
下面先看一个带通滤波器的设计指标图
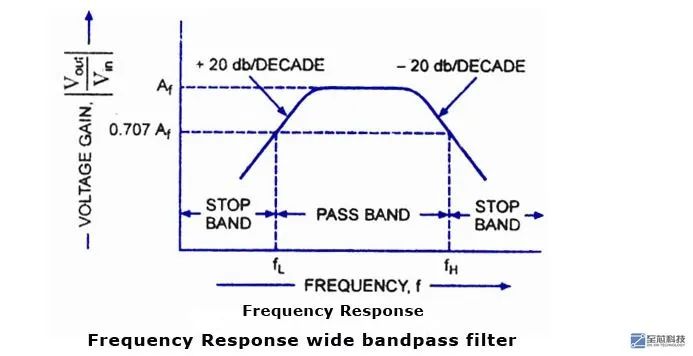
经典滤波器的指标主要就分为4个,即通带截止频率,阻带截止频率,通带最大衰减,阻带最小衰减。关于这4个参数的意思想必大家都已经很熟了,要不然信号处理这门课**的是白学了,这里就不再多说,我们直接看之前的题目,题目要求我们的过渡带频率分别为100~300HZ,500~700HZ,对应带通滤波器的参数我们可以很清楚的知道我们要设计的滤波器的截止频率,即
通带截止频率为300HZ,500HZ,阻带截止频率为100HZ,700HZ。即我们的通带是300~500HZ,而我要求的的信号,是由100,400,800HZ频率的三个信号叠加而成,因此,若这个信号通过滤波器之后,应该是阻带内的信号滤除,只保留通带内的信号才对,所以最后我们要验证的就是,通过滤波器滤波后的信号的波形,要跟信号频率为400HZ的信号波形一致,才证明我们的滤波器设计正确。好了,好像我们根据这个图只知道这点东西,想真正设计出来还是差的远呢,下面的知识将涉及到滤波器原理部分。
2、浅谈FIR滤波器原理
FIR滤波器呢,就是我们所学的有限脉冲响应滤波器。他的特点就是他的单位脉冲响应是有限长的。其实我们设计FIR滤波器就是设计他的单位脉冲响应,因为一个信号经过滤波器输出,得到的输出信号就是输入信号与滤波器单位脉冲响应的线性卷积,输入信号通过与单位脉冲响应信号之间的乘积累加运算得到输出信号,因此我们设计各式各样的单位脉冲响应信号,就可以根据我们的要求滤除和保留信号,从而达到滤波的目的。
所谓系统函数,即对单位脉冲响应进行Z变换,从Z变换的表达式我们知道,FIR滤波器就是单位脉冲响应与输入信号的乘积累加,每一个乘法器系数就是一个FIR系数。
3、关于线性相位
线性相位是FIR滤波器的一大特点,这里的线性相位,指的是我们的滤波器具有线性相位,而前面说了,我们的FIR滤波器,其实就是指单位脉冲响应,因此我们要设计成具有线性相位的FIR滤波器,其实就是让我们的单位脉冲响应满足线性特点?那怎么满足呢?因为一个序列,我们对其求频率响应之后得到的是他的幅频响应与相频响应,因此,我们需要从相频响应入手

即让斜率保证是一个常数的情况下进行讨论,这个讨论的过程相信大家书本上都有,因此这里就不必多讲,希望大家自己好好看一下,还是那句话,只有强大的理论支持,你才有信息做一名合格的工程师。我这里就做一个总结吧,主要分为四种情况,即FIR滤波器的线性特性由单位脉冲响应的长度N与单位脉冲响应的对称情况决定:
第一类线性相位(即h(n)关于n = (N-1)/2 偶对称) :
滤波器长度N为奇数时,h(n)的幅频响应关于w= 0,π,2π三点偶对称,适合设计成各种滤波器,即低通,高通,带通,带阻
滤波器长度N为偶数时,h(n)的幅频响应关于w = 0,2π偶对称,关于w = π奇对称,不适合设计成高通和带阻滤波器
第二类线性相位 (即h(n) 关于n = (N-1)/2 奇对称):
滤波器长度N为奇数时,h(n)的幅频响应关于w= 0,π,2π三点奇对称,只能实现带通滤波器
滤波器长度N为偶数时,h(n)的幅频响应关于w = 0,2π奇对称,关于w = π偶对称,不适合设计成低通和带阻滤波器
所以,要想保证FIR滤波器是线性相位,就必须得让单位脉冲响应是对称的,不管是偶对称还是奇对称,在保证了对称的前提下去确定滤波器长度的奇偶性,从而确定合适的幅频响应的形状,从而设计合适的滤波器,但是由于第一类线性相位没有初始相位,而且当滤波器长度为奇数的情况下,我们可以设计成各种滤波器,所以第一类线性相位比较常用。
4、利用窗函数法设计FIR滤波器
窗函数设计方法是最常见,最常用,最简单的滤波器设计方法,他的基本思路是逼近的思想,为什么呢?我们先来看他的设计方法。
窗函数的设计方法,首先我们需要给出一个理想的滤波器的频率响应,例如我们的上面的题目给出的,我要设计一个带通滤波器,首先我需要给出一个理想的带通滤波器的频率响应。
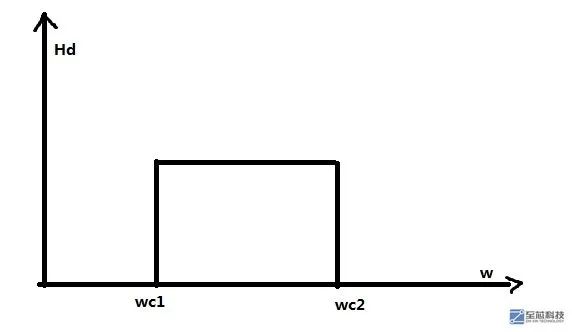
因为是理想滤波器,所以就没有什么过渡带所言了,所以wc1就是300HZ,wc2就是500HZ,我们将理想带通滤波器的频率响应进行逆傅里叶变换,从而得到我们理想带通滤波器的单位脉冲响应,如果我们用这个单位脉冲响应设计出的带通滤波器,当然就是最标准,无误差的滤波器了,但是现实与理想总是还有些差距的,将理想带通滤波器的频率响应进行逆傅里叶变换之后,我们知道,这是个无限长的序列,而我们FIR滤波器是有限长序列,因此我们可以利用一个窗函数和这个理想的单位脉冲响应进行相乘
这样就相当于将原来无限长序列变为了有限长,长度就是窗函数的长度,在窗内的序列得以保留,窗外的序列就被剔除,得到一个有限长单位脉冲响应序列,也是对原来理想单位脉冲响应的一个近似,正是由于这个近似,导致我们设计的滤波器与理想滤波器之间的误差,这是由于窗函数的截断引起的,称为截断效应。

图中,hd(n)是理想滤波器的单位脉冲响应,w(n)是窗函数序列,二者相乘得到我们要设计的实际滤波器的单位脉冲响应,将其进行傅里叶变换,观察他的频率响应,我们知道,时域相乘,就是频域相卷,理想滤波器的频率响应我们之前提过,窗函数的频域函数根据不同的窗函数,频域表达式都不同,以矩形窗为例,两者相卷得
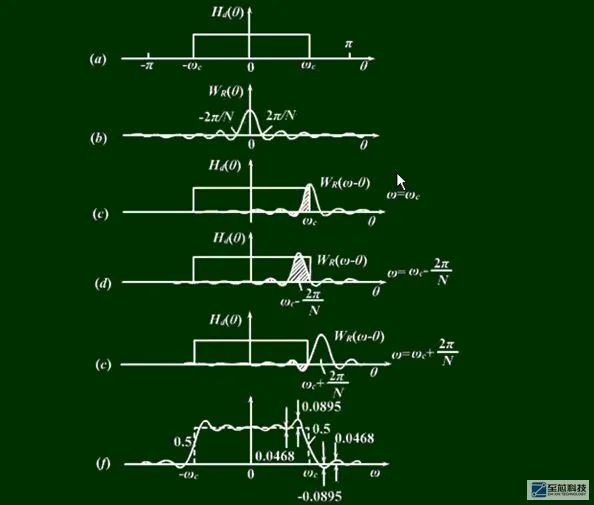
根据这个图我们知道,两个函数相卷,就是两个函数的乘积累加,也就是两个函数图像的左右移动的公共面积之和。
图b是窗函数的幅度特性函数,中间那部分叫做主瓣,旁边的小圆弧叫做旁瓣
图c表明,将窗函数的图像左右移动到图c的位置时,正好窗函数的一半图像在理想滤波器函数内,一半在外,此时对应图f中的过渡带的中点,即幅度衰减0.5那个点
图d和图e表明,当函数移动到这两个位置时,公共面试是最大,最小的,此时在频域上的反应结果就是图f的两个肩峰,一个正肩峰,一个负肩峰,肩峰高度为H(0)的8.95%。
从图f中,我们可以隐隐约约看到了滤波器的影子了,虽然没有理想滤波器那么标准,但也是近似逼近了,由于我们是将理想的滤波器的单位脉冲响应进行截断处理,因此函数在左右移动的时候会产生波纹,这种现象就叫做吉布斯效应。
5、关于吉布斯效应
为了更好的逼近理想滤波器,我们需要让他的过渡带更窄,阻带下降更快,波纹越小,阻带衰减越大。我们从课本上知道,主瓣宽度是由窗函数的长度决定的,以矩形窗为例,他的主瓣宽度为4π/N,主瓣宽度就是滤波器的过渡带带宽,为了减小过渡带带宽,是不是可以通过增大N值来解决吉布斯效应呢?增大N值仅仅可以减小过渡带,但是不能很好的减小波纹幅度,要想更好地逼近理想滤波器,还要从窗函数的形状上下手
6、常用窗函数
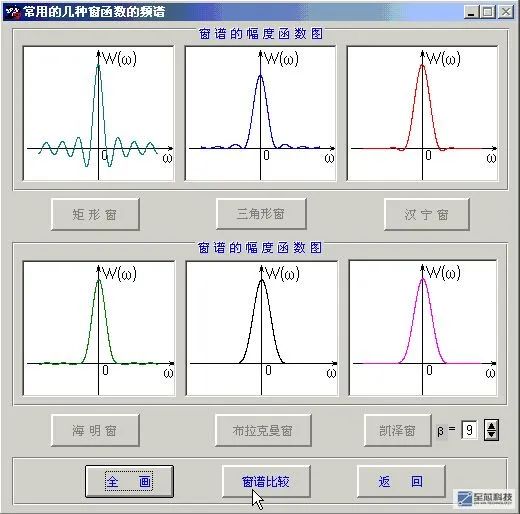
我们可以看到,不同的窗函数的幅频特性还是区别很大的,一般情况下,旁瓣幅度越小,滤波器的波纹越小,旁瓣幅度下降越大,滤波器阻带衰减越快,主瓣宽度越小,那么滤波器的过渡带就越窄,然而鱼和熊掌不能兼得,从上图我们看到,要得到幅度小的旁瓣,是要牺牲主瓣宽度为代价的,而主瓣宽度小的,往往旁瓣幅度大,例如矩形窗。
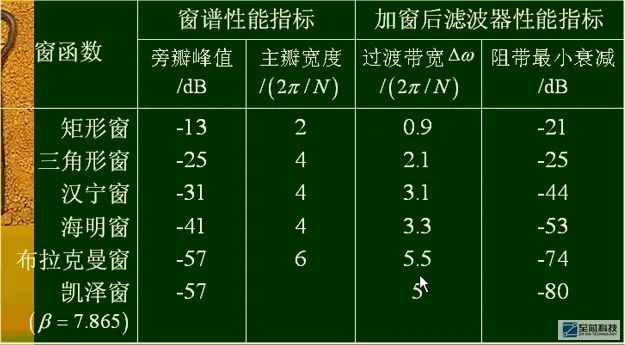
这些东西大部分都是我们课本上的了,就不必多说,我们接下来看工程应用部分。
7、FIR滤波器的matlab设计
其实matlab已经给我们提供了强大的函数工具箱,我们只需要给定参数就可以设计出符合我们要求的滤波器,但是对于理论知识,我们还是要知道的,即使我们用不上那些复杂的推导过程,但是至少我们知道他是怎么来的,对我们的设计也有一定的知道意义。
上面那个题目我要求大家用kaiserord函数来获得滤波器参数,先来讲一下这个函数
kaiserord 函数的语法:
[n,wn,beta,filtype] = kaiserord [f,a,dev,fs] ;
即将滤波器的过渡带参数f,幅度参数,通带阻带误差,采样频率送给kaiserird函数,将会返回我们需要的滤波器参数,包括滤波器阶数,截止频率,凯塞窗参数beta以及滤波器类型。
例如,根据题目要求,过渡带带宽分别为100~300HZ,500~700HZ,阻带允许误差为0.02,通带允许误差为0.01,采样频率为2000HZ 的带通滤波器

解释一下a是怎么设置的,参数a是一个向量,第一个参数表示0~fc(1)频段的幅度情况,第二个参数表示fc(2)~fc(3)频段内的幅度特性,以此类推,例如我们要设计带通滤波器,设置a = [0 1 0],就是指在频段300~500hz内是通带,其他为阻带。
函数返回的值为最小的滤波器阶数,并不是滤波器长度,滤波器长度 N = n+1;
题目还要求设计成等波纹最优滤波器,即等波纹切比雪夫滤波器,至于最优滤波器的推导过程十分复杂,大家可以自己去看书,这里只是调用matlab自己的函数库,从而为我们节省了大量的时间,设计最优滤波器的函数是cfirpm
函数语法为:
fir_pm = cfirpm (n,fpm,mag);
n为滤波器阶数,fpm跟上面的f类似,也是各个频带的参数,mag是各个频带的幅度参数,但是略有不同,例如我们要设计的带通滤波器:

要注意的是,参数mag必须是与fpm等长的向量,具体含义大体为,第一个参数为起始幅值,第二个参数是0~fpm(1)频带的参数,第三个参数是fpm(1)~fpm(2)频带的参数,以此类推。例如我们设计的带通滤波器,就是mag = [0 0 1 1 0 0 ],即表示在300~500HZ频带内为通带,其余为阻带。
至于归一化处理,就是相当于将所有频率放到一个合适的坐标系里来观察,并不影响滤波器性能。
通过这个函数,我们就相当于设计出了一个滤波器,函数返回值fir_pm就是滤波器系数,也就是单位脉冲响应,我们要做的就是讲这些系数送入FPGA,只要有了滤波器系数,剩下的就只剩下乘积累加了,但是这些系数不利于FPGA计算,FPGA适合的是二进制的运算方式,因此我们需要将这些系数进行量化,前面提到了,量化位数为12bit

至于语法为什么是这样,基础不好的朋友可以自行去补课,也可以联系本人,简单说一下,因为我们这里的计算全部是有符号数的形式,因此需要将数转化成16进制补码的形式,保证在通过FPGA进行运算的时候的符号是正确的。
当然我们还要观察这个滤波器设计的情况,就要看他的幅频响应,通过绘图来观察

源程序中我分别用凯塞窗和最优滤波器来设计了这个带通滤波器,大家可以比较一下两种方法的区别,最终设计好的滤波器幅频响应图
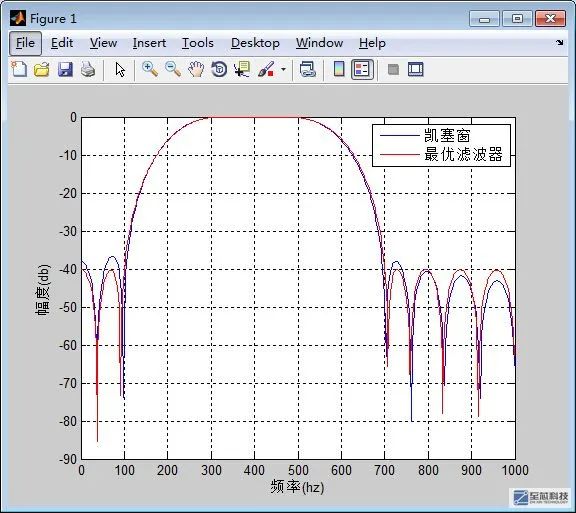
我们可以看到,最优滤波器的旁瓣是等波纹的,而凯塞窗在旁瓣幅度方面跟最优滤波器还是略第一个档次,要不然人家为什么要叫最优滤波器呢
8、信号产生
根据题目要求,我们需要产生一个由三个频率叠加而成的信号,让这个信号通过滤波器进行滤波。对于信号的产生过程这里没必要多少,大家自己去写,我们可以先通过matlab来仿真一下,这个信号经过滤波器滤波后是什么样子的。
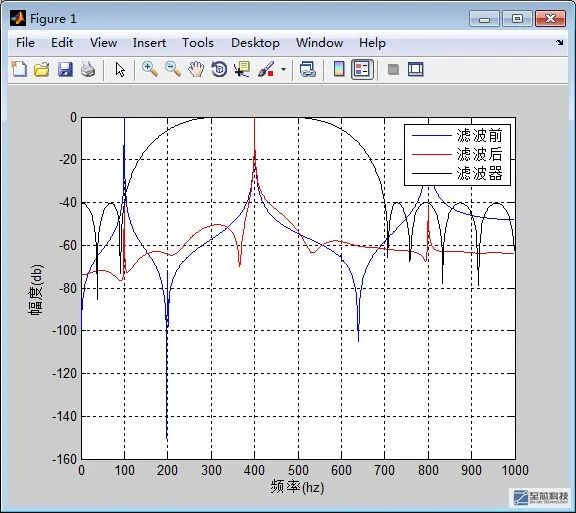
可以看到,三个信号叠加而成的合成信号的频段分为三个部分,即100,400,800HZ,分别对应三个信号,这是在频域观察到的,由于在时域他们是相互重叠的,因此不好滤除,但是到了频域,他们确是分开的,因此可以通过滤波器滤除。我们的滤波器仅仅允许400HZ的信号通过,因此经过滤波器滤波后,红色线只剩下频段为 400HZ的频段了,我们将经滤波器滤除后的时域信号显示一下
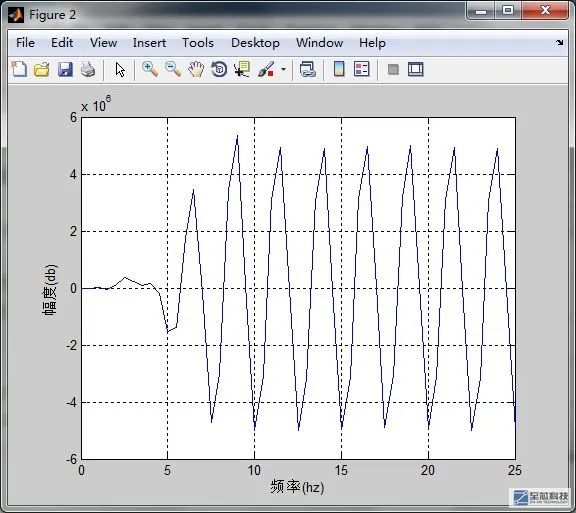
可以看到,经滤波器滤波后,频率为400hz的信号被保留,时域信号是完整的正弦波,有些朋友可能会说,怎么会有失真呢?失真可能是有点,但是还是由于我们的采样频率不够高,都是还原的波形不够圆滑。还有人可能会说,根据时域采样定理,不是采样频率大于2倍的信号频率就可以被还原成原始信号吗?但是我们这里并不是还原原始信号,这还是数字信号,只是将滤波后离散的点用线连起来了而已。
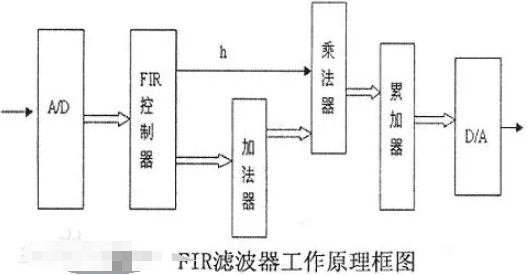
9、FIR滤波器的FPGA实现
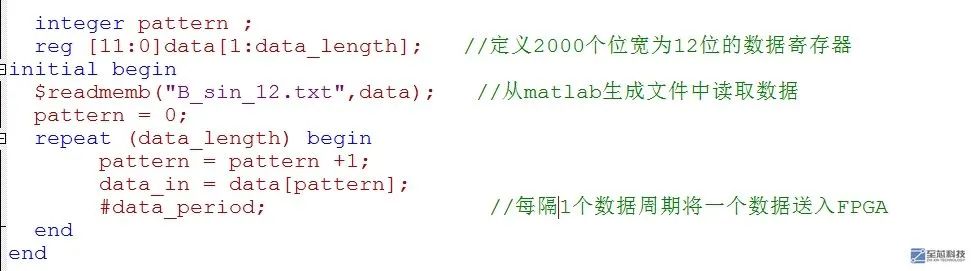
好了,matlab仿真成功,剩下的就需要在FPGA上实现了,在FPGA上实现什么呢?前面我们已经得到了滤波器的系数,只要有了滤波器系数,剩下的不就是乘积累加了么,所以,我们需要在FPGA上实现信号的乘积累加,即对叠加信号和滤波器系数的乘积累加。滤波器系数已经有了,那么信号在哪呢?我们可以利用matlab将生成的叠加信号以2进制的形式写到一个文件中去,注意是12bit量化。那也就是说,每一个数据是由12位二进制组成的,根据采样频率,共有2000个数据,这2000个数据,全部用二进制补码表示,共同组成了一个叠加信号,至于怎么将数据写到文件中去,这里不解释,大家可以自己下载代码,自己学习
有了滤波器系数,有了输入信号,下面就可以设计硬件电路了,根据线性卷积的原理,需要将输入信号和滤波器系数进行乘积累加,由于我们的滤波器是线性相位的,即关于(N-1)/2 偶对称,这里我们设计的滤波器阶数为23,这个参数是由kaiserord函数返回来得到的,也就是说滤波器长度是24,而且又是偶对称的,所以只需要将输入信号的对称位数与滤波器系数的前半部分相乘即可,即只需乘到h(11)即可,因为后面的都是跟前面的重复的。
data_a 《= { shift_reg [0] [11] , shift_reg [0] } ;
data_b 《= { shift_reg [23] [11], shift_reg [23] };
hn 《= 12‘hfec; //hn(0)
注意,这里定义了24个位宽为12的移位寄存器,即每隔一段时间输入一个位宽为12bit的数,这个时间就是一个数据周期,在数据周期内要完成一个数的线性卷积运算,由于我们的滤波器长度是24,这里定义寄存器长度也为24。
data_a 是累加器的加数a,将输入的第一个数据与他的最高位位,即符号位拼接来扩展为13位的数据,因为两个12位的数相加,为了保证符号位不溢出,需要13位的位宽,而要得到13位的输出结果,因为我们是调用加法器IP核的,所以输入的数据位宽也要是13位位宽。
data_b是移位寄存器的最高位内的数据,将移位寄存器的最高位与最低位相加,在跟滤波器系数相乘,同理将次低位与次高位相乘,等到一个数据的12位全部与滤波器系数相乘完毕之后,将数据输出,一个数据的滤波完成,接着送来下一个12位的数据,继续进行卷积运算,一直等到所有数据(2000个点)滤波完成。
hn是由matlab生成的滤波器系数,共有24个,全部是经过12bit量化后的由16进制数表示的,我们直接调用就行,由于他的对称性,我们只需要调用前12个即可,后12个参数跟前12个参数是对称的
上面这个过程需要进行11次,因为每次将两个数进行乘积,等到11次累乘结束,就要将这11累乘的结果累加并输出,得到一个点的滤波结果

注意:这里我等到cnt = 1的时候才进行累加输出,为什么呢?由于我们的乘法器和加法器需要时间进行运算,当cnt = 11的时候理论上所有数据运算完毕,但是我们还是要通过行为仿真,看一下最后一次累加什么时候结束,等最后一次累加结束后,我们再将数据输出,并将累加器清零
乘法器的两个参数,一个是前面加法器的和,另一个是滤波器系数hn,加法器输出是13位位宽,滤波器系数是12位位宽,因此乘法器输出为25位位宽,由于是将23个乘法器输出的结果进行累加,因此,为了保证数据不溢出,要设置一个比较保险的位宽来存取这个累加结果,这里我们选用30位位宽
10、testbench的书写
这里仅简单介绍一点,关于testbench的书写主要涉及两方面,一个是将信号读出来送入FPGA仿真,一方面是将经FPGA滤波后的数据输出,再供matlab调用仿真
将数据输出到文件**matlab调用
always @(posedge data_clk) begin
if(rst_n == 1)
$fdisplay(fir_dataout_file,“%d”,fir_dataout);
end
好了,一切准备就绪,我们通过modelsim来仿真我们的滤波器,看信号滤波前和滤波后的差距
可以看到,滤波前的信号杂乱无章,是因为他是有三个频率的信号叠加而成,而经过滤波器滤波后的信号变得井井有条,此时modelsim已经将FPGA输出的数据以txt文件的格式保存起来,如果我们用matlab将这些数据读回,做一下时域和频域信号的分析,就可以验证我们滤波器设计的正确性

执行上面的代码得到滤波后的信号的频域波形与时域波形
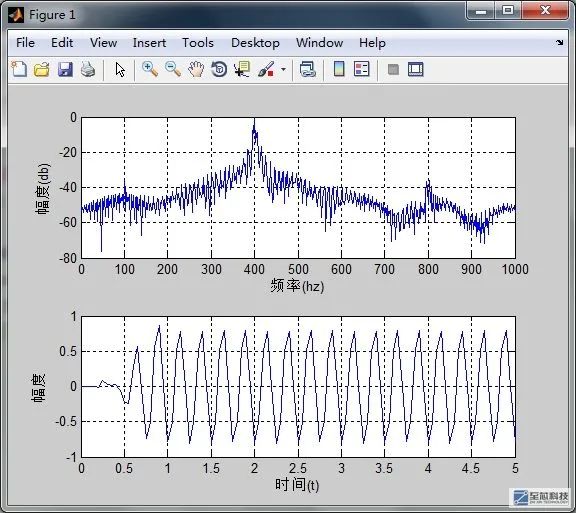
根据这个波形我们可以看到,经过FPGA设计的FIR滤波器滤波后的信号时域波形,跟我们之前用matlab仿真时的时域波形相同,频域波形可以很明显的看到,只有频率为400hz的信号被保留下来,100hz与800hz的信号已被滤除,从matlab仿真结果来看,我们设计的滤波器还是符合要求的。
编辑:lyn
-
FPGA
+关注
关注
1634文章
21830浏览量
608040 -
滤波器
+关注
关注
161文章
7919浏览量
179507 -
数字信号
+关注
关注
2文章
983浏览量
47778
原文标题:零基础学FPGA (二十九)滤波器开篇,线性相位FIR滤波器的FPGA实现
文章出处:【微信号:gh_9d70b445f494,微信公众号:FPGA设计论坛】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
如何区分IIR滤波器和FIR滤波器
iir滤波器和fir滤波器的优势和特点
基于matlab FPGA verilog的FIR滤波器设计
matlab与FPGA数字信号处理系列 Verilog 实现并行 FIR 滤波器
DSP教学实验箱_DSP算法实验_嵌入式教程:4-3 有限冲激响应滤波器(FIR)算法(CCS显示)
Matlab生成fir滤波器抽头系数
Vivado 使用Simulink设计FIR滤波器
高通滤波器、低通滤波器、带通滤波器怎样测幅频特性?
Vivado经典案例:使用Simulink设计FIR滤波器




 如何利用matlab设计一个线性相位FIR带通滤波器,并在FPGA上实现
如何利用matlab设计一个线性相位FIR带通滤波器,并在FPGA上实现
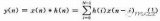











评论